【刷题日记】笔试经典编程题目(五)
大家好,我是白晨,一个不是很能熬夜,但是也想日更的人✈。如果喜欢这篇文章,点个赞,关注一下白晨吧!你的支持就是我最大的动力!
文章目录
- 前言
- 笔试经典编程题目(五)
-
- 1.星际密码
- 2.树根
- 3.跳台阶扩展问题
- 4.快到碗里来
- 5.不用加减乘除做加法
- 6.三角形
- 7.猴子分桃
- 8.奇数位上都是奇数或者偶数位上都是偶数
- 9.求正数数组的最小不可组成和
- 10.有假币
- 11.最难的问题
- 12.因子个数
- 后记
前言
虽然还有很多课,但是也不能忘了写编程题呀。
白晨总结了大厂笔试时所出的经典题目,本周题型包括动态规划,条件控制,数学归纳,算法等,难度比上周有些许增长,主要是数学归纳的题目,如果找不到规律,暴力破解很难不超时。真是万物起源数学。
都是很有代表性的经典题目,适合大家复习和积累经验。
这里是第五周,大家可以自己先试着自己挑战一下,再来看解析哟!
笔试经典编程题目(五)
1.星际密码
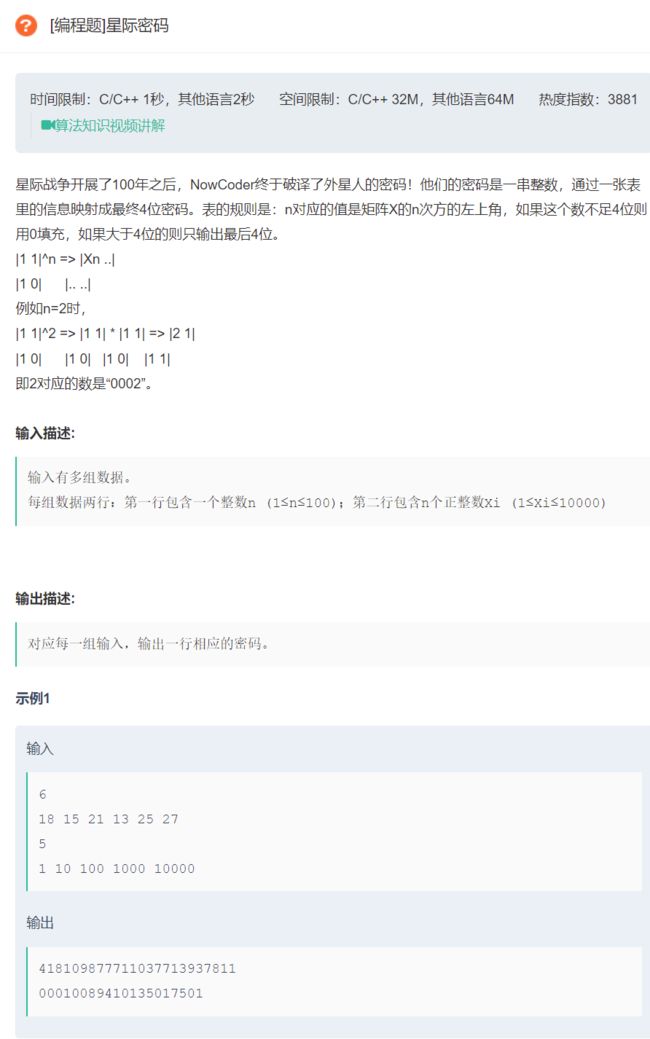
原题链接:星际密码
这道题的题目描述是真的恶心,一道很易懂的题愣是被描述的很难。我来翻译一下这道题:
存在一个矩阵 A = [ 1 1 1 0 ] A = \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right] A=[1110] ,给定一个整数 n ( 1 ≤ n ≤ 10000 ) n(1\leq n\leq10000) n(1≤n≤10000),求 A n A^n An 左上角元素 a ( 1 , 1 ) a_{(1,1)} a(1,1) ,并将其转换为4位密码:如果 a ( 1 , 1 ) a_{(1,1)} a(1,1) 不足四位,那么需要在前面补0,如果多余四位,取后四位。
题目会给
x个整数 n n n,求这x个4位密码。A 2 = [ 1 1 1 0 ] ∗ [ 1 1 1 0 ] = [ 2 1 1 1 ] − − > a ( 1 , 1 ) = 2 − − > 四 位 密 码 : 0002 A^2 = {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right] } * {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]} = \left[ \begin{matrix} 2 & 1 \\ 1 & 1 \end{matrix} \right] --> a_{(1,1)} = 2 --> 四位密码:0002 A2=[1110]∗[1110]=[2111]−−>a(1,1)=2−−>四位密码:0002
算法思想:
- 乍一看这就是很简单的矩阵乘法,直接模拟矩阵乘法实现,但是这个矩阵有一些规律:
A = [ 1 1 1 0 ] A = {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right] } A=[1110]
A 2 = [ 1 1 1 0 ] ∗ [ 1 1 1 0 ] = [ 2 1 1 1 ] A^2 = {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right] } * {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]} = \left[ \begin{matrix} 2 & 1 \\ 1 & 1 \end{matrix} \right] A2=[1110]∗[1110]=[2111]
A 3 = [ 2 1 1 1 ] ∗ [ 1 1 1 0 ] = [ 3 2 2 1 ] A^3 = {\left[ \begin{matrix} 2 & 1 \\ 1 & 1 \end{matrix} \right] } * {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]} = \left[ \begin{matrix} 3 & 2 \\ 2 & 1 \end{matrix} \right] A3=[2111]∗[1110]=[3221]
A 4 = [ 3 2 2 1 ] ∗ [ 1 1 1 0 ] = [ 5 3 3 2 ] A^4 = {\left[ \begin{matrix} 3 & 2 \\ 2 & 1 \end{matrix} \right] } * {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]} = \left[ \begin{matrix} 5 & 3 \\ 3 & 2 \end{matrix} \right] A4=[3221]∗[1110]=[5332]
A 5 = [ 5 3 3 2 ] ∗ [ 1 1 1 0 ] = [ 8 5 5 3 ] A^5 = {\left[ \begin{matrix} 5 & 3 \\ 3 & 2 \end{matrix} \right] } * {\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]} = \left[ \begin{matrix} 8 & 5 \\ 5 & 3 \end{matrix} \right] A5=[5332]∗[1110]=[8553]
- 我们取左上角的元素
1, 2, 3, 5, 8,满足 f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n) = f(n-1)+f(n-2) f(n)=f(n−1)+f(n−2) ,是斐波那契数列,所以我们可以将问题转换为求斐波那契数列。 - 特别注意:如果直接算斐波那契数列,那么会在几百位的时候超过整形最大的存储范围,解决方法:只保留斐波那契数的后四位作为密码即可。
代码实现:
#include 2.树根
原题链接:数根
特别注意:题目说是给一个正整数,但是其长度已经超过了整形的范围,必须要用字符串接收。
法一:字符串加法+递归
算法思想:
- 字符串加法思路:
我们可以模拟正常的加法,从个位开始,逐位相加,模拟过程中要注意的是:
- 我们取出字符串的每一个元素都是字符,所以不能直接将其相加,必须要减去
'0'才能得到这个数的真实值。- 当一个数的每一位都已经遍历完了,如果另一个数还没遍历完,则在这个数的高位补0。
- 如果两个数字之和大于等于10,要进位。
- 每次向要返回字符串插入一个本次相加得到的个位数。
- 最后得到的返回字符串是反的,我们要将其反转。
class Solution { public: string addStrings(string num1, string num2) { int i = num1.size() - 1, j = num2.size() - 1; int flag = 0; string ret; // 当给定的数字没有遍历完或者要进位时,进入循环 while (i >= 0 || j >= 0 || flag != 0) { // 判断一个数是否已经遍历完 int val1 = i >= 0 ? num1[i] - '0' : 0; int val2 = j >= 0 ? num2[j] - '0' : 0; // 看有没有进位 // flag == 1,有进位,反之,无进位 flag = flag == 1 ? val1 + val2 + 1 : val1 + val2; // 将本次相加的个位数插到返回字符串后 ret += flag % 10 + '0'; flag /= 10; i--; j--; } // 反转字符串 reverse(ret.begin(), ret.end()); return ret; } };
- 利用字符串加法将字符串每一位相加,如果最后得到的字符串长度大于1,进入递归;反之,则返回。
代码实现:
#include
法二:整形相加+迭代
算法思想:
- 虽然题目给定的数最高可达1000位,但是每一位相加的总和最多为9000,完全可以用一个整形
ret存放。 ret += s[i] - '0',同样遍历字符串的每一位求和。- 如果
ret大于9,继续进行每一位求和,直到小于10。
代码实现:
#include 另一种实现:
#include 3.跳台阶扩展问题
原题链接:跳台阶扩展问题
算法思想:
- 既然它叫跳台扩展问题,那么它一定是个数学问题,我们可以探究一下规律。
- 假设有n级台阶,那么上这n级台阶的方式有:
- 先上1级,再上一次直接上n-1级。
- 先上2级,再上一次直接上n-2级。
- 先上1级,再上一次直接上n-3级。
- …
- 先上n-1级,再上1级。
- 直接上n级。
- 那么假设上n级台阶的方法数为
f(n),根据上面的逻辑我们可以得到递推公式为:
f ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . . . . + f ( n − 1 ) + 1 f(n) = f(1) + f(2) + f(3) + ......+f(n-1)+1 f(n)=f(1)+f(2)+f(3)+......+f(n−1)+1
- 再来探究一下规律:
| 台阶数/n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 方法数/f(n) | f(1) = 1 | f(2) = f(1) + 1 = 2 | f(3) = f(1) + f(2) + 1 = 4 | f(4) = f(1) + f(2) + f(3) = 8 | f(5) = f(1) + f(2) + f(3) + f(4) = 16 |
- 得到普遍公式: f ( n ) = 2 n − 1 f(n) = 2^{n-1} f(n)=2n−1
代码实现:
class Solution {
public:
int jumpFloorII(int number) {
return pow(2, number - 1);
}
};
也可以直接用位操作:
class Solution {
public:
int jumpFloorII(int number) {
return 1 << (number - 1);
}
};
4.快到碗里来
原题链接:快到碗里来
法一:字符串相乘
算法思想:
-
由于2^128已经超过了整形最大的范围,所以我们使用字符串存储所给数据,并且利用字符串相乘得到碗的周长。
-
字符串相乘具体思路:
思路一:模拟竖式+加法实现先来看例子中的乘法用竖式如何计算:
我们发现,从右到左,
num2每一位都需要乘以num1,并且每乘完一次num1所得的数字的权重要乘10。
num2每一位乘num1都是个位数*num1,所以我们可以先把个位数乘num1的结果保存起来,用的时候直接调用。得到
num2每一位乘num1的字符串后,保存起来,最后和竖式一样,依次相加每一位的结果,得到最后的答案。class Solution { public: // 复用上题的加法 string Add(const string& num1, const string& num2) { string ret; int add = 0; int end1 = num1.size() - 1, end2 = num2.size() - 1; while (end1 >= 0 || end2 >= 0 || add != 0) { int n1 = end1 >= 0 ? num1[end1--] - '0' : 0; int n2 = end2 >= 0 ? num2[end2--] - '0' : 0; add = n1 + n2 + add; ret += add % 10 + '0'; add /= 10; } reverse(ret.begin(), ret.end()); return ret; } string multiply(string num1, string num2) { // 出现0时,直接返回"0" if (num1 == "0" || num2 == "0") return "0"; int len1 = num1.size(), len2 = num2.size(); // 保存 0 ~ 9 乘 num1 的值 vector<string> save(10); // 保存num2每一位乘num1的值 vector<string> ret(len2 + 1); // 0乘任何数都为0 save[0] = "0"; // 保存最后的返回值 ret[len2] = "0"; // 记录权重 int pos = 0; // 保存 0 ~ 9 乘 num1 的值 for (int i = 1; i < 10; ++i) { save[i] = Add(save[i - 1], num1); } // 保存num2每一位乘num1的值 for (int i = len2 - 1; i >= 0; --i) { int val = num2[i] - '0'; ret[i] = save[val]; // 根据权重在字符串后面补0 for (int j = 0; j < pos; ++j) ret[i] += '0'; // 每乘完一个数,权重加一 pos++; } // 整体加起来 for (int i = 0; i < len2; ++i) { ret[len2] = Add(ret[len2], ret[i]); } return ret[len2]; } };
思路二:优化竖式+模拟乘法
- 首先,我们先来探讨一下 m位数乘n位数得到的结果为多少位数。
由上式可得,最后相乘得到的数字最长为 m + n m+n m+n ,所以我们可以预先开辟一个 m + n m+n m+n 长度的数组来存放这个数字。
由于要使用乘法进行模拟,所以我们可以优化一下我们的竖式乘法
通过上面的例子我们可以得到优化后竖式的具体做法:
- 将原来一次乘一个整形的步骤拆解为一次一个数只乘一个数
- 这样就不用担心溢出问题
- 并且我们可以将相乘的结果直接加到上述数组对应的位上,就如同上面的竖式一样
- 进行完全部的竖式运算后,再处理得到的数组,该进位进位,保证每一位上都是个位数。
- 再将数组转换为字符串后返回。
代码实现:
class Solution { public: string multiply(string num1, string num2) { if (num1 == "0" || num2 == "0") return "0"; int m = num1.size(), n = num2.size(); vector<int> num(m + n); string ret; // 模拟每一位乘每一位 for (int i = n - 1; i >= 0; --i) { int val2 = num2[i] - '0'; for (int j = m - 1; j >= 0; --j) { int val1 = num1[j] - '0'; int mul = val1 * val2; // 将乘来的结果加到对应的位上 num[i + j + 1] += mul; } } // 进位 for (int i = m + n - 1; i > 0; --i) { num[i - 1] += num[i] / 10; num[i] %= 10; } // 判断有没有最高位 int i = num[0] == 0 ? 1 : 0; for (; i < m + n; ++i) { ret += num[i] + '0'; } return ret; } };
代码实现:
#include
法二:浮点数计算
算法思想:
- 如果基础比较好的同学可能还记得:
float的范围为 − 2 128 ∼ 2 128 -2^{128} \sim 2^{128} −2128∼2128,也即-3.40E+38 ~ +3.40E+38;double的范围为 − 2 1024 ∼ 2 1024 -2^{1024} \sim 2^{1024} −21024∼21024,也即-1.79E+308 ~ +1.79E+308
- 符合题目数据的范围,但是为了精度,这里我们选择用double存储。
- 但是这个方法是有缺陷的,范围再大就可能保证不了精度或者甚至超过范围,而相比之下第一种方法则没有这个风险。
代码实现:
#include 5.不用加减乘除做加法
原题链接:不用加减乘除做加法
算法思想:
- 异或操作:如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
- 异或操作本身可视为将两个数加在一起,但是没有进位,比如:
3 ^ 5 --> 011 ^ 101 = 110,这里没有算上第一位的进位。 - 那么进位如何处理呢?
- 二进制同位置上如果出现两个1就相当于进位了,所以进位我们可以用
&来获得,但是获取之后为了使进位进到上一位,必须将结果左移一位,比如:3 & 5 --> 011 & 101 --> 001 ,左移一位,010。 - 接下来,相当于要获取 110 + 001 的和,怎么获取呢?
- 很简单,重复前两步,直到进位为0时,此时异或以后的值就是最后的和。
具体实例:
- 我们以
5 + 13举例,先将其化为2进制5-->0101 , 13-->1101。 5 ^ 13 = 1000 , (5 & 13) << 1 = 10101000 ^ 1010 = 0010 , (1000 & 1010) << 1 = 100000010 ^ 10000 = 10010 , (0010 & 10000) << 1 = 0- 此时
10010-->18就为最终答案。
代码实现:
class Solution {
public:
int add(int a, int b) {
while (b)
{
int tmp = a ^ b;
b = (unsigned)(a & b) << 1;// 这里注意如果不加强转leetcode会出现莫名的溢出导致执行错误
a = tmp;
}
return a;
}
};
6.三角形
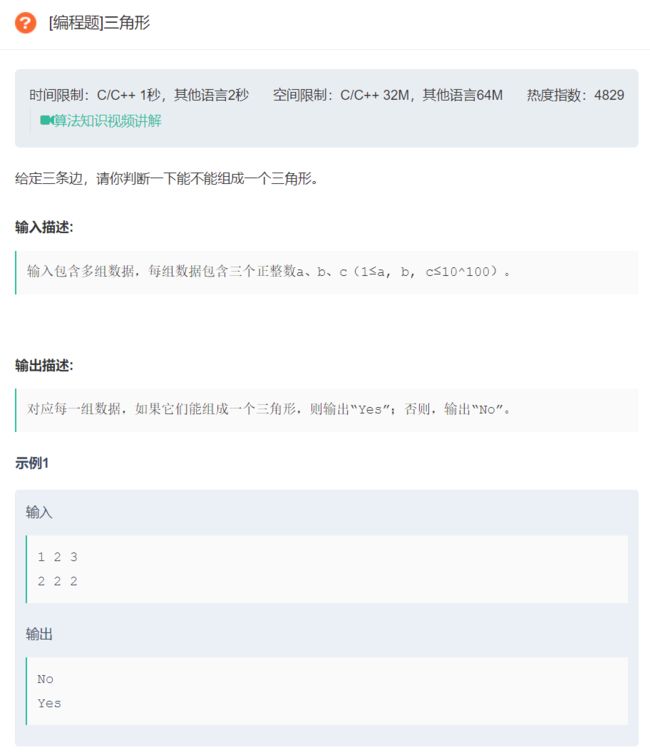
原题链接:三角形
法一:浮点数
算法思想:
- 如何判断三边是否可以组成一个三角形:
任意两边之和大于第三边。 - float的范围为 − 2 128 ∼ 2 128 -2^{128} \sim 2^{128} −2128∼2128,也即 − 3.40 E + 38 ∼ 3.40 E + 38 -3.40E^{+38} \sim 3.40E^{+38} −3.40E+38∼3.40E+38;double的范围为 − 2 1024 ∼ 2 1024 -2^{1024} \sim 2^{1024} −21024∼21024,也即 − 1.79 E + 308 ∼ 1.79 E + 308 -1.79E^{+308} \sim 1.79E^{+308} −1.79E+308∼1.79E+308,所以可以用double类型变量存储题目条件。
代码实现:
#include
法二:字符串相加+比较
算法思想:
- 上面的方法是钻了一个漏子,因为double数据越靠近极限范围,精度越小,所以我们不能保证精度,这里只是牛客网没有检查出来而已。
- 所以,我们还是老老实实用字符串相加+比较实现一下。
- 字符串相加思路:
✈
原题链接:字符串相加模拟:
我们可以模拟正常的加法,从个位开始,逐位相加,模拟过程中要注意的是:
- 我们取出字符串的每一个元素都是字符,所以不能直接将其相加,必须要减去
'0'才能得到这个数的真实值。- 当一个数的每一位都已经遍历完了,如果另一个数还没遍历完,则在这个数的高位补0。
- 如果两个数字之和大于等于10,要进位。
- 每次向要返回字符串插入一个本次相加得到的个位数。
- 最后得到的返回字符串是反的,我们要将其反转。
class Solution { public: string addStrings(string num1, string num2) { int i = num1.size() - 1, j = num2.size() - 1; int flag = 0; string ret; // 当给定的数字没有遍历完或者要进位时,进入循环 while (i >= 0 || j >= 0 || flag != 0) { // 判断一个数是否已经遍历完 int val1 = i >= 0 ? num1[i] - '0' : 0; int val2 = j >= 0 ? num2[j] - '0' : 0; // 看有没有进位 // flag == 1,有进位,反之,无进位 flag = flag == 1 ? val1 + val2 + 1 : val1 + val2; // 将本次相加的个位数插到返回字符串后 ret += flag % 10 + '0'; flag /= 10; i--; j--; } // 反转字符串 reverse(ret.begin(), ret.end()); return ret; } };
代码实现:
#include 7.猴子分桃
原题链接:猴子分桃
算法思想:
以上思路来自于牛客网网友
代码实现:
#include 8.奇数位上都是奇数或者偶数位上都是偶数
原题链接:奇数下标都是奇数或者偶数下标都是偶数
法一:快慢指针法
算法思想:
- 用一个步长为1的慢指针
s遍历数组。 - 当s为奇数,arr[s]为偶数时,让快指针
f从s + 1出发寻找奇数,遇到奇数即交换arr[s]和arr[f]; - 当s为偶数,arr[s]为奇数时,让快指针
f从s + 1出发寻找偶数,遇到偶数即交换arr[s]和arr[f]。 - 特别注意:
s与f在任何时候都必须小于数组长度。
代码实现:
#include
法二:双重查找法
算法思想:
- 上面算法的劣势是一次只能保证一个数排到正确位置上,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
- 我们参考快速排序找数交换的方法,设定一个偶数下标指针
even和一个奇数下标指针odd,以步长为2来移动它们。直到至少一个指针越界,表示已经完成了奇数下标都是奇数或偶数下标都是偶数。 - 在移动的过程中,如果奇数下标对应的数为奇数或者偶数下标对应的数为偶数,那么移动对应的指针。
- 否则就交换此时两个不满足条件的元素。
代码实现:
#include 9.求正数数组的最小不可组成和
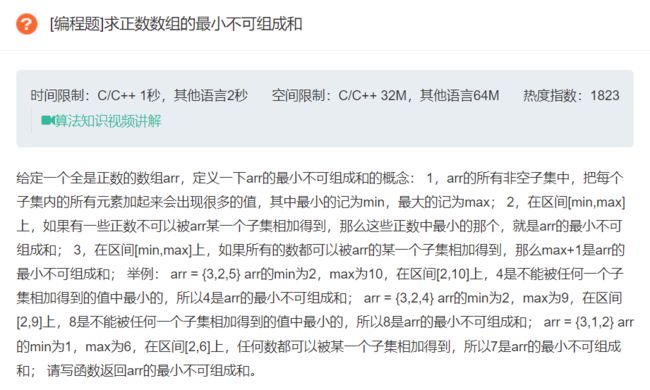
原题链接:求正数数组的最小不可组成和
这道题其实是背包问题的变式。
算法思路:
- 首先,先来了解一下背包问题的思路:
原题链接:背包问题
class Solution { public: int backPackII(int m, vector<int>& A, vector<int>& V) { if (A.empty() || V.empty() || m < 1) return 0; const int N = A.size() + 1; const int M = m + 1; vector<vector<int> > ret; ret.resize(N); // 初始化 for (int i = 0; i != N; ++i) { ret[i].resize(M, 0); } for (int i = 1; i < N; i++) { for (int j = 1; j < M; j++) { // 如果背包总空间都不够放第i个物品,则放 i 个物品和 放 i - 1 个物品的情况相同 if (j < A[i - 1]) ret[i][j] = ret[i - 1][j]; // 如果空间足够放第i个物品,则要判断是否要放入,详见上文解析 else ret[i][j] = max(ret[i - 1][j], ret[i - 1][j - A[i - 1]] + V[i - 1]); } } return ret[N - 1][m]; } };优化算法:
class Solution { public: int backPackII(int m, vector<int>& A, vector<int>& V) { if (A.empty() || V.empty() || m < 1) return 0; const int M = m + 1; // 包容量 const int N = A.size() + 1; // 物品数量 vector<int> ret(M, 0); for (int i = 1; i < N; i++) { // 上面的算法在计算第i行元素时,只用到第i-1行的元素,所以二维的空间可以优化为一维空间 // 但是如果是一维向量,需要从后向前计算,因为后面的元素更新需要依靠前面的元素未更新(模拟二维矩阵的上一行的值) // 并且我们观察到,本行的元素只需要用到上一行的元素,所以从前往后,从后往前都相同 // 且用到上一行元素的下标不会超过本行元素的下标 for (int j = m; j >= 0; j--) { if (j >= A[i - 1]) ret[j] = max(ret[j], ret[j - A[i - 1]] + V[i - 1]); } } return ret[m]; } };
-
这道题中的隐含条件是物品的价值和物品的体积相等。
-
状态转移方程:如果 j − a r r [ i − 1 ] > = 0 j - arr[i - 1] >= 0 j−arr[i−1]>=0,也就是空间足够放下第i个物品时,
dp[i][j] = max(dp[i - 1][j - arr[i - 1]] + arr[i - 1], dp[i - 1][j]),也就是在放入这个物品和不放入中选一个。反之,放不下这个物品时,
dp[i][j] =dp[i - 1][j]。 -
返回值:数组的最后一行就是当前背包空间数,所能拿到的最大价值。由于本题中,价值等于空间,所以最大价值也就是背包的空间数。
在最后一行的数组中,从下标为min开始,如果有价值不等于空间的,就为最小组成数。
如果价值都等于空间,那么返回max+1。
eg. v = {3, 2, 4},w = {3, 2, 4} ,max = 9,min = 2。我们将其视为,背包空间最大为9,最多可以取3个物品。
横行为背包空间数,纵行为前i件物品。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 2 | 0 | 0 | 2 | 3 | 3 | 5 | 5 | 5 | 5 | 5 |
| 3 | 0 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 9 |
从最后一行,下标为2(min)开始找,发现下标为8时,价值等于7,不相等,所以8为最小不可组成数。
代码实现:
class Solution {
public:
int getFirstUnFormedNum(vector<int> arr, int len) {
int Max = 0, Min = arr[0];
for (auto e : arr)
{
Max += e;
if (e < Min)
Min = e;
}
// 多开辟一行一列,方便存储
vector<vector<int>> v(arr.size() + 1, vector<int>(Max + 1, 0));
for (int i = 1; i < v.size(); ++i)
{
// 从下标为最小值开始遍历即可
for (int j = Min; j <= Max; ++j)
{
if (j - arr[i - 1] >= 0)
{
v[i][j] = max(v[i - 1][j - arr[i - 1]] + arr[i - 1], v[i - 1][j]);
}
else
{
v[i][j] = v[i - 1][j];
}
}
}
for (int i = Min; i <= Max; ++i)
{
if (i != v[arr.size()][i])
return i;
}
return Max + 1;
}
};
优化一下空间:
class Solution {
public:
int getFirstUnFormedNum(vector<int> arr, int len) {
int Max = 0, Min = arr[0];
for (auto e : arr)
{
Max += e;
if (e < Min)
Min = e;
}
vector<int> v(Max + 1, 0);
for (int i = 0; i < len; ++i)
{
for (int j = Max; j >= Min; --j)
{
if (j - arr[i] >= 0)
v[j] = max(v[j - arr[i]] + arr[i], v[j]);
}
}
for (int i = Min; i <= Max; ++i)
{
if (v[i] != i)
return i;
}
return Max + 1;
}
};
10.有假币
原题链接:有假币
这道题是一道很经典的益智题,也是一道数学思想大于实现的题目,换句话说,没有思路,这道题是基本不可能做出来的。
算法思路:
-
先来看一些例子:
-
当
n = 1时,不用称,这个硬币是假币。 -
当
n = 2时,我们将其分为两堆,1个、1个放天平两端,轻的就是假币,总共需要1次 -
当
n = 3时,随机抽出2个放到天平两端,也就是(1,1,1)这样分,如果天平平衡,则剩下1个就是假币,否则天平中较轻的是假币,总共需要1次 -
当
n = 4时,分成(1,1,2),将1,1放到天平两端,如果平衡,则假币在2这一堆,我们按n = 2再称一次,总共就是两次;如果不平衡,那么只用一次就可得到假币。注意题目条件:
最短时间下,最多要称几次一定可以称出来?,也就是考虑在最优算法下最坏的情况,所以n = 4时,总共要称2次。 -
当
n = 5时,分成(2,2,1),将2,2放到天平上,考虑最坏情况,就是天平不平衡,再转换为n = 2的问题求解。综上,总共需要称两次。 -
当
n = 6时,分成(2,2,2),将2,2放到天平上,考虑最坏情况,再转换为n = 2的问题求解。综上,总共需要称两次。 -
当
n = 7时,分成(2,2,3),将2,2放到天平上,考虑最坏的情况,天平平衡,将问题进一步转化为n = 3求解,也就是两次。
-
-
总结一下上面的例子:
-
首先,要将
n分为3堆,再选取这三个数中最大的数Max作为下一步的n。 -
MAX = n / 3 + (n % 3 > 0) -
重复上述过程,直到
n == 1。
代码实现:
递归:
#include 迭代:
#include 11.最难的问题
原题链接:最难的问题
算法思路:
这道题没有什么难度,具体见代码。
代码实现:
#include 12.因子个数
原题链接:因子个数
算法思路:
- 这道题的意思就是求一个数的全部的因子,所以我们可以直接使用求质数的方法进行求解。
- 具体见代码解析:
代码实现:
#include 后记
本次题目难度有一些提高,这次题目主要集中在数学归纳这个上限很高的题目,比较考验大家的逻辑思维,相信大家做完会有所收获。
这个是一个新的系列——《笔试经典编程题目》,隶属于【刷题日记】系列,白晨开这个系列的目的是向大家分享经典的笔试编程题,以便于大家参考,查漏补缺以及提高代码能力。如果你喜欢这个系列的话,不如关注白晨,更快看到更新呀。
本文是笔试经典编程题目的第五篇,如果喜欢这个系列的话,不如订阅【刷题日记】系列专栏,更快看到更新哟
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦!
如果这篇文章有帮到你,还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧!喜欢白晨【刷题日记】系列的话,不如关注白晨,以便看到最新更新哟!!!
我是不太能熬夜的白晨,我们下篇文章见。