最小生成树-贪心算法

概念引入：

（1）子图：从原图中选中一些定点和边组成的图，称为原图的子图。
（2）生成子图：选中一些边和所有定点组成的图，称为原图的生成子图。
（3）生成树：如果生成子图恰好是一棵树，则成为生成树。
（4）最先生成树：权值之和最小的生成树，则称为最小生成树。
所以最小生成树满足：1.权值最小，2.含有图中每一个结点。
最小生成树算法和前面学到的dijkstr求最短路径的算法及其相似，==
最短路径算法==-从原点出发-找到一个距离当前最近的结点（则该节点就是原点到该结点的最短距离）- 我们用这条边去跟新和其他结点的最短距离，下次再从剩下的未访问的结点中去选最小值，依次推倒下去每次找到的最小结点都是离原点最短距离。
*最小生成树算法-prim *(采用的是避圈法)-先找到离原点最近距离的结点i，再去找该结点到其他结点的距离比如将这些边值存入dist[]数组中，则这个数组中存储的是集合S到V-S集合的结点当然一维数组里面只能存储一个值，那么这个值就是具有最小值的结点，每次过滤dis[]数组中的值的时候我们需要选取的是最小的边值。
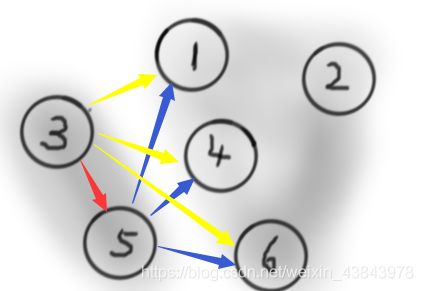
图解：从原点出发假设有三条边

这三条边分别是3->1, 3->4,3->5。
选择权值最小的一条边：

用红色箭头标记为以确定的边值。这样V集合里面有集合有V={3,5}，用阴影标记出来。假设结点的全集为T则剩余结点为：T-V
则V与T-V直接的连线如下：

可以看到这之间有很多的线而，比如以4为结点的边有3->4,5->4而我们只会选择其中权值较小的一条，在和1，6进行比较。

找到权值最小的一条为5->6.
依次类推便可以得到所有的边：

数据结构：
T[][]临界矩阵存储图中的信息，S[]表示以选中的结点集合，lowcost[i]表是到i结点的权值最小的边，cost[i]表示i结点的前驱结点。
prim()函数,1.完成lowcost初始化，2.挑选出离集合T最近的定点x，3.x定点到其他定点的最小值更新lowcost[]。

代码如下：

#include 
#include 
using namespace std;
#define INF 10000
const int maxn= 1000+5;
int T[maxn][maxn];//用于储存结点信息
bool s[maxn];//结点集合
int lowcost[maxn],costest[maxn];//lowcost表示到该结点的最短的边的权值，costest保存的是每个结点的前驱结点。
void  Prim(int u0,int n)//u0：原点 n:结点个数
{
    s[u0]=true;//原点标记为0
    for (int i = 1; i <=n ; ++i)
    {
        if(i!=u0)
        {
            lowcost[i]=T[u0][i];
            s[i]= false;
            costest[i]=u0;
        }
        else
            lowcost[i]=0;
    }//完成初始化
//初始化要做的事情有：先将该结点到其他结点距离初始化给lowcost数组，将所有的结点的前驱标记为u0.
    for (int i = 1; i <=n ; ++i) {
        int temp = INF;
        int t = u0;

        for (int i1= 1; i1 <= n; i1++) {
            if (!s[i1] && temp > lowcost[i1]) {
                temp = lowcost[i1];
                t = i1;
            }
        }//挑选集合S中最小的边的令一个结点

        if (t == u0)
            break;
        s[t] = true;
        for(int j=1;j<=n;j++)
        {
            if(!s[j]&&T[t][j]<lowcost[j])//该处便是与最短路径的差别之处
            {
                lowcost[j]=T[t][j];//更新出该结点到其他结点的最小距离
                costest[j]=t;//规定结点的前驱为t
            }
        }//for
    }//for
}
int main()
{
    int u,v;//u:表示结点数，v:表示边数
    int m1,m2,value;
    int u0;
    cin>>u>>v;
    for (int i=1;i<=u;i++)
    {
        for (int j = 0; j <= u; ++j)
        {
            T[i][j]=INF;
        }
    }//初始化结点值为无穷大
    for(int i=1;i<=v;i++)
    {
        cin>>m1>>m2>>value;
        T[m1][m2]=T[m2][m1]=value;//无向图
    }
    cin>>u0;
    Prim(u0,u);//u0是原点，u则表示结点个数
    int ans=0;
    for(int i=1;i<=u;i++)
    {
        cout<<lowcost[i]<<endl;
    }
    cout<<"最小花费为:"<<ans;
}

采用优先队列对该算法进行优化：

#include 
#include 
#include 
using namespace std;
#define INF 10000
const int maxn= 1000+5;
int T[maxn][maxn];
bool s[maxn];
int lowcost[maxn],costest[maxn];//lowcost表示到该结点的最短的边的权值，costest保存的是每个结点的前驱结点。

struct Node{
    int u;//结点
    int step;//距离
    Node(){};

    Node (int a,int b)
    {
        u=a;
        step=b;
    }
    bool operator < (const Node &a)
    const {
        return step>a.step;//从大到小
    }//可以将这一部分当作一个模板
};

void  Prim(int u0,int n)//u0：原点 n:结点个数
{
    priority_queue<Node>Q;
    for (int i = 1; i <=n ; ++i) {
        lowcost[i]=INF;
    }//初始化
    
    Q.push(Node(u0,INF));
    //将源节点加入队列中
   while(!Q.empty())
   {
        Node it=Q.top();
        Q.pop();
        int t=it.u;
        if(s[t])
            continue;
        s[t]= true;
        for(int j=1;j<=n;j++)
        {
            if(!s[j]&&T[t][j]<lowcost[j])//
            {
                lowcost[j]=T[t][j];//更新出该结点到其他结点的最小距离
                //costest[j]=t;//规定结点的前驱为t
                Q.push(Node(j,lowcost[j]));
            }
        }//for
    }//while
}//Prim

int main()
{
    int u,v;//u:表示结点数，v:表示边数
    int m1,m2,value;
    int u0;
    cin>>u>>v;
    for (int i=1;i<=u;i++)
    {
        for (int j = 0; j <= u; ++j)
        {
            T[i][j]=INF;
        }
    }//初始化结点值为无穷大
    for(int i=1;i<=v;i++)
    {
        cin>>m1>>m2>>value;
        T[m1][m2]=T[m2][m1]=value;//无向图
    }
    cin>>u0;
    //输入原点
    Prim(u0,u);//u0是原点，u则表示结点个数
    int ans=0;
    for(int i=1;i<=u;i++)
    {
        cout<<lowcost[i]<<endl;
    }//计算最小花费
    cout<<"最小花费为:"<<ans;
}

利用优先队列可以减少每次选最小结点消耗的时间，同最短路径是一个道理，先存储一个源节点，然后更新该结点到每一个结点的距离，存入优先队列中，优先队列中u元素，表示到该节点的最短的九零而不是从该点出发的到别的结点的最短距离。

---

用Kurskal算法来构造最小生成树：
将这n个定点看成是n个孤立的连通分支。它首先将所有的边按权值从小到大排序，然后我们依次选择边只要边数不满主n-1我们就一直贪心下去，而在将边加入集合T的时候我们不能要边构成一个环。代码如下：

#include
#include
using namespace std;
const int maxn=1000;
int nodest[maxn];
int n;
struct edge{
 	int u;//前驱结点
 	int v;//后继结点
	int w;//权重
 	bool operator<(edge const &a)
 	const{
  		return w<a.w;
 	}//按从小大大排序
}e[maxn*maxn];
void Init()
{
 	for(int i=1;i<=n;i++)
 	{
  		nodest[i]=i;//初始化每个结点为一个结点集 
 	}
 }
int Merge(int a,int b)
{
 	int p=nodest[a];//选出来a所属的结点集 
 	int q=nodest[b];//选出来b所属的结点集 
 	if(p==q)
  		return 0;//如果两者相同则不用左任何处理 
 	for(int i=1;i<=n;i++)
 	{		
  	if(nodest[i]==q)
   		nodest[i]=p;//将a的节点集合全部改为b的结点集 
 	}
 	return 1;
}
int main()
{
 	int m; 
 	int ans=0;
 	cout<<"请输入图的结点数和边数:"<<endl;
 	cin>>n>>m;
 	Init();//初始化每一个结点 
 	for(int i=1;i<=m;i++)
 	{
  		cin>>e[i].u>>e[i].v>>e[i].w;
 	}//输入边值的信息 
 	
 	sort(e+1,e+m+1);
 	//排序
 	int n1=n;
 	for(int i=1;i<=m;i++)
 	{
  		if(Merge(e[i].u,e[i].v))//如果可以合并就将该集合加入结点集中 
  		{
  			// cout<
   			ans+=e[i].w;
   			n1--; 
   			if(n1==1)//当发生了n-1次合并即完成了最小生成树的工作 
    				break; 
  		}//if
 	}//while
 cout<<"最下的权值为:"<<endl;
 cout<<ans;
}

---

算法分析：这里我们判断是否是一个集合中的结点时，浪费了大量的时间，每次都要遍历每一个结点。我们课以通过构建一个堆来减低时间复杂度，具体做法如下：

#include
using namespaace std;
const int maxn=100;
int father[maxn];
int n,m;

struct dege{
    int u;
    int v;
    int w;
    bool operator<(const edge &a)
    const{
        return w<a.w;
    }
}e[maxn*maxn];

void Init()
{
    for(int i=1;i<=n;i++)
        father[i]=i;
}

int Find(int a)
{
    if (a!=father[a])//不是根结点则继续向上寻找更结点
        father[a]=Find(father(a));//将沿途中的所有结点的父亲全部该为根结点的值,(起到了压缩路径的作用)，这样做可以降低树的高度。

    return father(a);
}

int Merge(int a,int b)//判断结点是否可以合并
{
    int p = find(a);//查找a的根结点
    int q = find(b);//查找b的根亲结点
    if(p==q)//如果两结点的父亲相同则证明两则再向量会构成回路
        return 0;
    else
    {
        if(p<q)//让小结点赋值给大结点，这样会令结集构成一颗树,小结点在上面.
            father[q]=p;
        else
            father[p]=q;
    }
}

int main()
{
    Init();//完成结点集的初始化
    int ans=0;
    cout<<"请输入结点数和边数:"<<endl;
    cin>>n>>m;
    for (int i = 1; i <=m ; ++i) {
        cin>>e[i].u>>e[i].v>>e[i].w;
    }
    sort(e+1,e+m+1);//从数组为1才开始赋值的+1
    int n1=n;
    for (int i = 1; i <=m ; ++i) {
        if(Merge(e[i].u,e[i].v)){//如果能合并就让合并次数减少一
            ans += e[i].w;
            n1--;
            if (n1 == 1)//边数已经够了
                break;
        }
    }
    cout<<"最少的花费是:"<<endl;
    cout<<ans;//输出结果
}