最短路问题（超详细~~）

最短路问题分类

最短路算法知识结构图

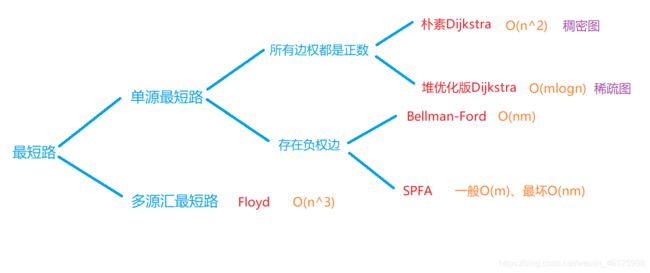
注：n为顶点数，m为边数
每种不同的情况都有相应最适合的算法，但不用拘泥于一定要用某个算法。
单源最短路：求一个点到其他所有点的最短距离
多源汇最短路：源 指 起点，汇 指 终点。任意两点间的最短距离（起点、终点不确定）
稠密图：m至少和n^2大致是一个级别 （稠密图用邻接矩阵存储）
稀疏图：m至少和n大致是一个级别 （稀疏图用邻接表存储）
重点：建图，如何把原问题抽象成一个最短路问题，如何定义点和边。

单源最短路

朴素Dijkstra算法

实现步骤：
1.初始化距离 dist[1] = 0，dist[i] = + ∞ （dist数组表示起点到i点的距离）
2.for循环 1~n循环n次 （s：当前已确定最短距离的点）
①找到不在s中的距离起点最近的点，赋给t O(n^2)
②把t加到s中去 O(n)
③用t来更新其他所有点的距离 O(m)（看从1号点<起点>到x的距离是否大于到t的距离，即dist[x] > dist[t] 如果是，则用t来更新)
找到没有确定最短路且距离起点最近的点，并通过这个点更新其他点到起点的最短距离（即以这个点为过渡点）
每次循环都可以确定一个点的最短距离，循环n次就可以确定每个点到起点的最短距离了。
模板

int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

典例——AcWing 849.Dijkstra求最短路I

#include 
#include 
#include 

using namespace std;

const int N = 510;

int n,m;
int g[N][N];  //邻接矩阵
int dist[N]; //当起点（1号点）到每个点的最短距离
bool st[N]; //标记当前点是否确定最短距离

int dijkstra()
{
	//初始化
    memset(dist,0x3f,sizeof(dist)); //除起点外全部初始化为正无穷
    dist[1] = 0;
    
    for(int i = 0; i < n; i ++ )
    {
        int t = -1;
        for(int j = 1; j <= n; j ++ )	//在没有确定最短路的所有点中找出距离起点最短的点
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
                
        st[t] = true; //标记t为已确定最短路
        
        for(int j = 1; j <= n; j ++ )   //用t更新其他店的最短距离
            dist[j] = min(dist[j],dist[t] + g[t][j]);
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;  //起点和终点不连通
    return dist[n];
}

int main()
{
    cin >> n >> m;
    
    memset(g,0x3f,sizeof g);
    
    while(m -- )
    {
        int a,b,c;
        cin >> a >> b >> c;
        
        g[a][b] = min(g[a][b],c);  //如果有重边，保留其中最短的一条
    }
    
    cout << dijkstra();
    
    return 0;
}

堆优化版Dijkstra

实现步骤：
1.初始化距离 dist[1] = 0，dist[i] = + ∞ （dist数组表示起点到i点的距离）
2.for循环 1~n循环n次 （s：当前已确定最短距离的点）
①找到不在s中的距离起点最近的点，赋给t <优化：用小根堆来找> O(1)
②把t加到s中去 O(n)
③用t来更新其他所有点的距离 O(mlogn) <利用堆更新每个点的时间复杂度为O(logn)>
整个算法的时间复杂度就可以优化成 O(mlogn)

m≤n^2 mlogm≤2mlogn 所以两种写法的时间复杂度是一个级别的， 所以堆优化版的Dijkstra一般是不需要手写堆的。

典例——AcWing 850.Dijkstra求最短路II

#include 
#include 
#include 
#include 

using namespace std;

const int N = 2e5;

int n,m;
int h[N],w[N],e[N],ne[N],idx; //邻接表存储
int dist[N];
bool st[N];

typedef pair<int,int> PII; //first存距离，second存结点编号

void add(int a,int b,int c)
{
    e[idx] = b,w[idx] = c,ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
	//初始化
    memset(dist,0x3f,sizeof(dist));
    dist[1] = 0;
    
    priority_queue<PII,vector<PII>,greater<PII>> heap; //小根堆
    heap.push({0,1});
    
    while(heap.size())
    {
        PII t = heap.top();
        heap.pop();
        
        int ver = t.second, distance = t.first; //定义ver为编号，distance为距离
        if(st[ver]) continue; 
        st[ver] = true;
        
        for(int i = h[ver]; i != -1; i = ne[i]) //用t更新其他点的最短距离
        {
            int j = e[i];
            if(dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];
                heap.push({dist[j],j});
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
	//初始化邻接表
    memset(h,-1,sizeof h);
    cin >> n >> m;
    while(m -- )
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    
    cout << dijkstra();
    
    return 0;
}

Bellman-Ford算法

思路：循环n次，每次循环都遍历所有边，每次都更新一个结点的最短距离，那么循环n次，就可以确定n个点的最短路。
注：存在最短路时，一般不存在负权回路，即使存在，这个负环也不能在这条路径上（若存在负权回路，那么每在这个回路上转一圈，距离都会减小，这样可以无限次停留在负权回路，导致距离变为 - ∞）
实现步骤：
1.初始化： dist[1] = 0，dist[i] = + ∞
2.for循环n次：
for循环m次：遍历所有边
dist[b] = dist[a] + w; （松弛条件）
时间复杂度O(nm)
循环n此后所有的边都满足 dist[b] ≤dist[a] + w （三角不等式）
迭代k次的含义：从1号点经过不超过k条边走到每个点的最短距离
找负环的方法：若果第n次迭代时，又更新了路径，说明存在长度≥n的最短路径。如果一个路径有n条边，那么就意味着有n+1个点，而图中一共只有n个点，由抽屉原理，就一定有两个点编号相同，那么这条路径上就一定存在环，而且是在更新过之后，所以这个环就一定是负环。所以这个算法可以用来找负环，方法就是看第n次是否有更新。（了解即可，一般找负环不用Bellman-Ford，而用SPFA）

典例——AcWing 853.有边数限制的最短路

#include 
#include 
#include 

using namespace std;

const int N = 510,M = 10010;

int n,m,k;
int dist[N],backup[N]; //backup 为备份数组，存储dist上一次的值

struct edges
{
    int a,b,w;
}edge[M];//存储边和权值

int bellman_ford()
{
	//初始化
    memset(dist,0x3f,sizeof(dist));
    dist[1] = 0;
    
    //迭代k次
    for(int i = 0;  i < k; i ++ )
    {
        memcpy(backup,dist,sizeof(dist)); //注1：备份
        
        for(int j = 0; j < m; j ++ )
        {
            int a = edge[j].a, b = edge[j].b, w = edge[j].w;
            dist[b] = min(dist[b],backup[a] + w); //用备份的值更新最短路
        }
    }
    
    if(dist[n] > 0x3f3f3f3f / 2) return -1; //注2
    return dist[n];
}
int main()
{
    cin >> n >> m >> k;
    for(int i = 0; i < m; i ++ )
    {
        int a,b,w;
        cin >> a >> b >> w;
        edge[i] = {a,b,w};
    }
    
    int t = bellman_ford();
    
    if(t == -1) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

思路解析：
这道题是Bellman-Ford算法的一个典型应用，而且此题只能用Bellman-Ford来做。
这道题的特殊性在于：要求的是从1号点到n号点最多经过k条边的最短距离，这里对边数做了限制，我们只需要迭代k此就可以了。
注1 memcpy(backup,dist,sizeof(dist))； 这里我们用backup数组来存储上一次迭代dist的值，防止发生串联，影响结果。

注2 if(dist[n] > 0x3f3f3f3f / 2) return -1; 这里判断最短路不存在的条件为什么不能写成 if(dist[n] == 0x3f3f3f3f )呢？
如果有负权边存在，我们在更新最短路的时候，可能会减掉一个数，∞减掉一个数，可能变成一个很大的而非∞的数，这时我们也认为，最短路是不存在的。

SPFA算法

SPFA适用于没有负环的图，但是绝大多数题目都是不存在负环的。SPFA算法是对上述Bellman-Ford算法的优化。Bellman-Ford是开两个循环，遍历每个点，每条边，这其中有很多重复的工作，SPFA对其进行了优化。
Bellman-Ford中dist[b] ≤dist[a] + w，dist[a]不一定是之前更新过的点，然而事实上，只有== 用之前被更新过的点去更新其他点，才会得到最短路 ==（只有一条路径上前面的点变小了，经过这个点的路径才会变小）。SPFA正是在这一点上进行了优化。
实现步骤：（用BFS来优化，队列中存储待更新的点）

1. 1号点入队
2. while(queue不空)
   ①取队头并入队（t = q.front() ）
   q.pop()；
   ②更新t的所有出边 t → b
   更新成功后，如果b不在队中，则入队。（b→queue）
   SPFA算法实现的过程和Dijkstra算法实现过程非常相似。
   典例——AcWing 851. spfa求最短路
   

#include 
#include 
#include 
#include 

using namespace std;

const int  N = 1e5 + 10,M = 1e5 + 10;

int n,m;
int h[N],e[N],w[N],ne[N],idx;
int dist[N];
bool st[N]; //标记第i个点是否在队列中，防止存储重复的点

void add(int a,int b,int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int spfa()
{
    memset(dist,0x3f,sizeof(dist));
    dist[1] = 0;
    
    queue<int> q; //存储待更新的点
    q.push(1); //1号点入队
    st[1] = true; 
    
    while(q.size()) //队列不空
    {
        int t = q.front(); //取队头
        q.pop();
        st[t] = false;
        
        for(int i = h[t]; i != -1; i = ne[i]) //更新t的临边结点
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if(!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    memset(h,-1,sizeof h);
    cin >> n >> m;
    while( m -- )
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    
    int t = spfa();
    
    if(t == -1) puts("impossible");
    else
    cout << t ;
    
    return 0;
    
}

SPFA算法判断负环

思路与上面所说的Bellman-Ford算法判断负环是相同的，这里我们另开一个cnt数组来存当前最短路的边数。每次更新边的同时，更新cnt，当== cnt ≥ n ==时，就说明存在负环。（多出来的边一定是负环，不然不会被更新到最短路中）

典例——AcWing 852.spfa判断负环

#include 
#include 
#include 
#include 

using namespace std;

const int N = 2010,M = 10010;

int n,m;
int h[N],e[M],w[M],ne[M],idx;
int dist[M],cnt[M];
bool st[N];

void add(int a,int b,int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int spfa()
{
    queue<int> q;
	//判断整个图中是否存在负环，需要将所有点入队
    for(int i = 1; i <= n; i ++ )
    {
        q.push(i);
        st[i] = true;
    }   
    
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;
        
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i]; 
                cnt[j] = cnt[t] + 1; //更新最短路上的边数
                
               if(cnt[j] >= n) return true;
               if(!st[j])
               {
                   q.push(j);
                   st[j] = true;
               }
            }
        }
    }
    
    return false;
}

int main()
{
    cin >> n >> m;
    memset(h,-1,sizeof h);
    while(m -- )
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(a,b,c);
    }
    if(spfa()) puts("Yes");
    else puts("No");
    
    return 0;
}

多源汇最短路

Floyd算法

原理：基于动态规划，状态表示（三维）：d[k,i,j]：从点 i 只经过1~k这些中间点到达点 j 的最短距离。
那么就有：d[k,i,j] = d[k-1,i,k] + d[k-1,k,j] （状态更新）
思路：我们可以把点i到j的方式归为两类

1. 从i 直接到 j；
2. 从i 经过 若干个点 到 j；
   模板：三重循环，d(i,j)表示从i到j的最短路的长度

//初始化：
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0; //Floyd算法要求不能存在负环
            else d[i][j] = INF;
//算法实现
void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

典例——AcWing 854.Floyd 求最短路

#include 

using namespace std;

const int N = 210,M = 20010,INF = 1e9;

int n,m,k;
int d[N][N];

void floyd()
{
    for(int k = 1; k <= n; k ++ )
        for(int i = 1; i <= n; i ++ )
            for(int j = 1; j <= n; j ++ )
            d[i][j] = min(d[i][j],d[i][k] + d[k][j]);
}
int main()
{
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= n; j ++ )
            if(i == j)  d[i][j] = 0;
            else d[i][j] = INF;
            
    while(m -- )
    {
        int x,y,z;
        cin >> x >> y >> z;
        
        d[x][y] = min(d[x][y],z);
    }
    
    floyd();
    while(k -- )
    {
        int x,y;
        cin >> x >> y;
        
        int t = d[x][y];
        if(t > INF/2) puts("impossible");
        //最短路不存在的判断条件写成t > INF/2，是因为可能存在负环，这个问题在前面有讲过。 
        else cout << t << endl;
    }
    
    return 0;
}

以上内容就是我总结的最短路问题的学习笔记。欢迎大佬们批评指正。