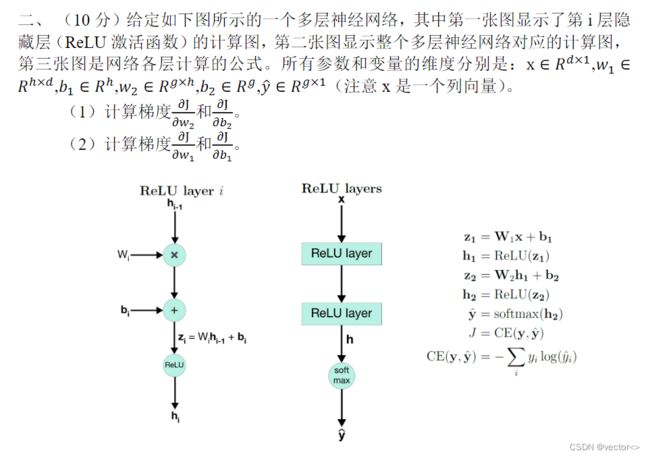
【一起入门DeepLearning】中科院深度学习_期末复习题2018-2019第二题：求梯度

专栏介绍：本栏目为 “2022春季中国科学院大学王亮老师的深度学习” 课程记录，这门课程与自然语言处理以及机器学习有部分知识点重合，重合的部分不再单独开博客记录了，有需要的读者可以移步 自然语言处理专栏和机器学习专栏。 如果感兴趣的话，就和我一起入门DL吧

2018-2019 学年第二学期期末试题

想了解梯度下降算法可以看这篇博客：【一起入门NLP】中科院自然语言处理第3课-前馈神经网络DNN（反向传播+梯度下降），这个题目完全是数学问题，一个很难算的数学问题下面是两位师兄的参考答案：

答案一：

$\frac{\partial J}{\partial w_2}=\frac{\partial J}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial h_2}\frac{\partial h_2}{\partial z_2}\frac{\partial z_2}{\partial w_2}=\left(\hat{y}\ast {\sum }_j{y}_j-y_i\right)\ast \mathrm{Relu}\left(z_2\right)\ast h_1$
$\frac{\partial J}{\partial b_2}=\frac{\partial J}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial h_2}\frac{\partial h_2}{\partial z_2}\frac{\partial z_2}{\partial b_2}=\left(\hat{y}\ast {\sum }_j{y}_j-y_i\right)\ast {\mathrm{Relu}}^{\prime }\left(z_2\right)$
$\frac{\partial J}{\partial w_1}=\frac{\partial J}{\partial h_2}\frac{\partial h_2}{\partial h_1}\frac{\partial h_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}=\left(\hat{y}\ast {\sum }_j{y}_j-y_i\right)\ast \mathrm{Relu}\left(z_2\right)\ast w_1\ast \mathrm{Relu}\left(z_1\right)\ast x$
$\frac{\partial J}{\partial b_1}=\frac{\partial J}{\partial h_2}\frac{\partial h_2}{\partial h_1}\frac{\partial h_1}{\partial z_1}\frac{\partial z_1}{\partial b_1}=\left(\hat{y}\ast {\sum }_j{y}_j-y_i\right)\ast \mathrm{Relu}\left(z_2\right)\ast w_1\ast \mathrm{Rel}{u}^{\prime }\left(z_1\right)$

---

答案二：
1. 将各层的计算公式按标量形式展开，下标中带括号的表示在矩阵或向量中对应的位置：
$z_{1(j)}={\sum }_{m=1}^d{W}_{1(jm)}{x}_{(m)}+b_{1(j)}$
$h_{1(j)}=\mathrm{Re}LU\left(z_{1(j)}\right)$
$z_{2(i)}={\sum }_{n=1}^h{W}_{2(in)}{h}_{1(n)}+b_{2(i)}$
$h_{2(i)}=\mathrm{Re}LU\left(z_{2(i)}\right)$
$y_{(i)}=\mathrm{soft}\max \left(h_{2(i)}\right)=\frac{e^{h_{2(i)}}}{{\sum }^g}{e}^{h_{2(i)})}$
$J=CE(y,\hat{y})=-{\sum }_{i^{\prime }=1}^g{y}_{\left(i^{\prime }\right)}\log \left({\hat{y}}_{\left(i^{\prime }\right)}\right)$

2. 计算交叉熵的导数：
$\frac{\partial J}{\partial \left({\hat{y}}_{\left(i^{\prime }\right)}\right)}=-\frac{y_{\left(i^{\prime }\right)}}{{\hat{y}}_{\left(i^{\prime }\right)}}$

3. Softmax求导：
当 $\mathrm{k}=\mathrm{i}$ 时
$$\frac{\partial {\hat{y}}_{(i)}}{\partial h_{2(k)}}=\frac{\partial {\hat{y}}_{(i)}}{\partial h_{2(i)}}=\frac{e^{h_{2(i)}}{\sum }_{i^{\prime }=1}^g{e}^{h_{2(i)}}-{\left(e^{h_{2(i)}}\right)}^2}{{\left({\sum }_{i^{\prime }=1}^g{e}^{h_{2(i)}}\right)}^2}={\hat{y}}_{(i)}\left(1-{\hat{y}}_{(i)}\right)$$
当 $k\ne i$ 时
$$\frac{\partial {\hat{y}}_{(i)}}{\partial h_{2(k)}}=-\frac{e^{h_{2(i)}}{e}^{h_{2(k)}}}{{\left({\sum }_{i^{\prime }=1}^g{e}^{h_{2(i)}}\right)}^2}=-{\hat{y}}_{(i)}{\hat{y}}_{(k)}$$
4. ReLU求导

$\frac{\partial \mathrm{ReLU}(x)}{\partial x}=u(x)$, 其中 $u(x)$ 为阶跃函数

(1)
$$\begin{array}{rl}& \frac{\partial J}{\partial W_{2(in)}}=\sum _{i^{\prime }=1}^g\frac{\partial J}{\partial {\hat{y}}_{\left(i^i\right)}}\frac{\partial {\hat{y}}_{\left(i^{\prime }\right)}}{\partial h_{2(i)}}\frac{\partial h_{2(i)}}{\partial z_{2(i)}}\frac{\partial z_{2(i)}}{\partial W_{2(in)}}\\ & =-\left[\frac{y_{(i)}}{{\hat{y}}_{(i)}}{\hat{y}}_{(i)}\left(1-{\hat{y}}_{(i)}\right)-\sum _{k\ne i}\frac{y_{(k)}}{{\hat{y}}_{(k)}}{\hat{y}}_{(i)}{\hat{y}}_{(k)}\right]u\left(z_{2(i)}\right)h_{1(n)}\\ & =u\left(z_{2(i)}\right)h_{1(n)}\left[-y_{(i)}\left(1-{\hat{y}}_{(i)}\right)+\sum _{k\ne i}{y}_{(k)}{\hat{y}}_{(i)}\right]\\ & =u\left(z_{2(i)}\right)h_{1(n)}\left[-y_{(i)}+\sum _{k=1}^g{y}_{(k)}{\hat{y}}_{(i)}\right]\\ & =u\left(z_{2(i)}\right)h_{1(n)}\left({\hat{y}}_{(i)}-y_{(i)}\right)\\ & \text{ 同理可知 }\\ & \frac{\partial J}{\partial b_{2(i)}}=u\left(z_{2(i)}\right)\left({\hat{y}}_{(i)}-y_{(i)}\right)\end{array}$$
(2)
$$\begin{array}{rl}& \frac{\partial J}{\partial w_{1(jm)}}=\sum _{i^{\prime }=1}^g\frac{\partial J}{\partial {\hat{y}}_{\left(i^{\prime }\right)}}\frac{\partial {\hat{y}}_{\left(i^{\prime }\right)}}{\partial h_{2(i)}}\frac{\partial h_{2(i)}}{\partial z_{2(i)}}\frac{\partial z_{2(i)}}{\partial w_{1(jm)}}\\ & =\sum _{i^{\prime }=1}^{g}u\left(z_{2\left(i^{\prime }\right)}\right)\left({\hat{y}}_{\left(i^{\prime }\right)}-y_{\left(i^{\prime }\right)}\right)W_{2\left(i^{\prime }j\right)}u\left(z_{1(j)}\right)\sum _{m=1}^d{x}_{(m)}\\ & =u\left(z_{1(j)}\right)\sum _{m=1}^d{x}_{(m)}\sum _{i^{\prime }=1}^{g}u\left(z_{2\left(i^{\prime }\right)}\right)\left({\hat{y}}_{\left(i^{\prime }\right)}-y_{\left(i^{\prime }\right)}\right)W_{2\left(i^{\prime }j\right)}\end{array}$$
同理可得
$$\frac{\partial J}{\partial b_{1(j)}}=u\left(z_{1(j)}\right)\sum _{i^{\prime }=1}^{g}u\left(z_{2\left(i^{\prime }\right)}\right)\left({\hat{y}}_{\left(i^{\prime }\right)}-y_{\left(i^{\prime }\right)}\right)W_{2\left(i^{\prime }j\right)}$$