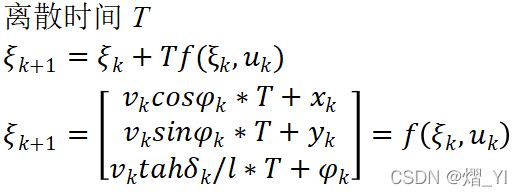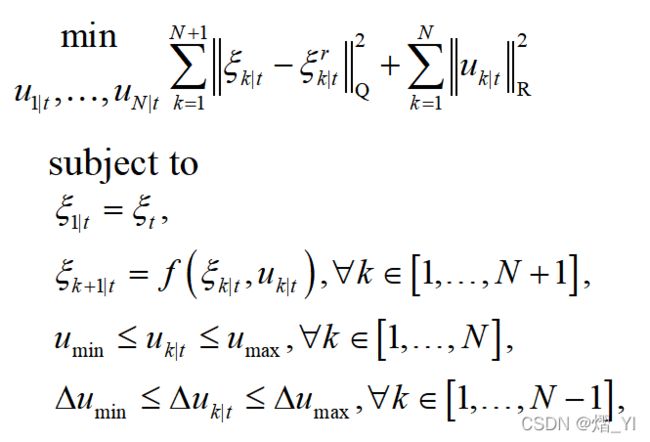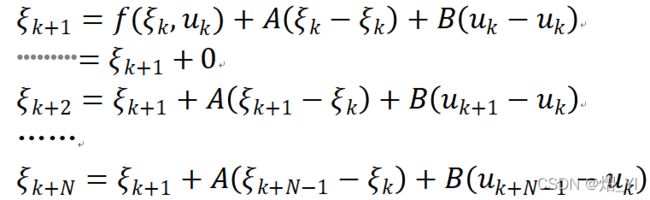Matlab/yalmip工具编写自动驾驶模型预测控制(MPC)代码
目录
前言
一、yalmip简介
二、车辆模型
1.车辆运动学模型
2.离散化
3.线性化
三、MPC优化问题定义
四、Matlab代码
五、结果
总结
前言
在无人驾驶的运动控制中,模型预测控制(MPC)算法得到了广泛使用,龚建伟的《无人驾驶车辆模型预测控制》一书对MPC算法进行了细致的讲解,并提供了代码,非常值得参考和学习。但书中各系数矩阵的推导对于初学者来说极难理解,代码结构也过于复杂,改动代码容易报错。采用yalmip工具可以直接添加约束和成本函数,在很大程度上简化代码,利于初学者对应理解MPC公式与代码,修改起来也较为容易。
一、yalmip简介
yalmip是由Lofberg开发的一种免费的优化求解工具。它是一个建模工具,甚至可以称为一种“语言”,通过这种“语言”来描述模型,然后再调用其他求解器(如quadprog、gurobi、fmincon等)来求解模型。其最大特色在于集成许多外部的优化求解器,形成一种统一的建模求解语言,提供了Matlab的调用API,减少学习者学习成本。
具体可以参考(原文链接:https://blog.csdn.net/s83625981/article/details/80076478),安装和学习使用yalmip。
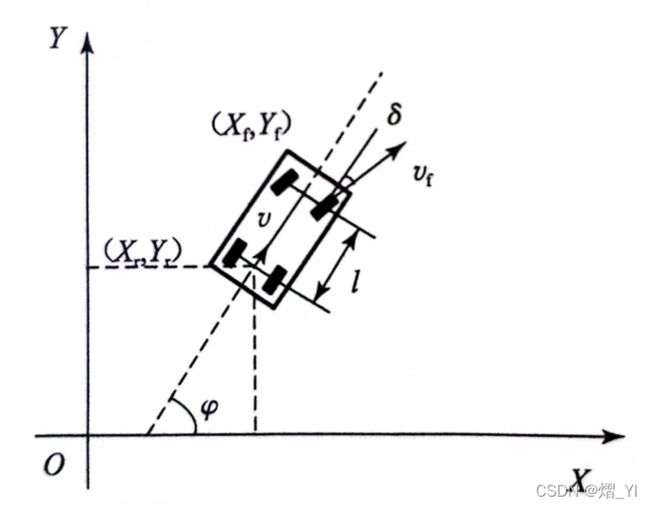
二、车辆模型
1.车辆运动学模型
2.离散化
3.线性化
这里使用针对状态轨迹的线性化方法(《无人驾驶车辆模型预测控制》(第二版)第五章代码所使用的方法),与第三、四章的存在参考系统的性线化方法略有不同,本质上区别不大,具体可以参考《无人驾驶车辆模型预测控制》(第一版)的介绍。
若使用较复杂的模型,可借助jacobian函数求解雅可比矩阵A,B
syms x y phi delta v L T
%x:横坐标;y:纵坐标;phi:航向角;delta:前轮偏角;
%v:速度;L:轴距;T:离散时间
kesi=[v*cos(phi);v*sin(phi);v*tan(delta)/L]*T+[x;y;phi];%离散化方程
X=[x,y,phi];%状态量
u=[v,delta];%控制量
A=jacobian(kesi,X)
B=jacobian(kesi,u)
三、MPC优化问题定义
程序目标是对轨迹进行跟踪,设计成本函数第一项:状态量与参考轨迹误差的平方,第二项:控制量的平方。约束依次为初始状态约束,车辆运动学模型,控制量约束,控制增量约束。优化问题如下所示:
四、Matlab代码
本文编写的代码主要为了对标《无人驾驶车辆模型预测控制》(第二版)第四章的代码,主体参照S函数形式编写,便于结合Carsim使用。以下主要介绍yalmip编写的MPC计算函数:
1.函数输入
A,B:模型(系统)矩阵;Q,R:权重矩阵;N:控制步长;kesi:当前状态量和控制量;state_k1:下一时刻状态量;umin,umax,delta_min,delta_max:控制量和控制增量约束矩阵;Ref: 参考轨迹;MPC_solver:求解器。
function [ x, uPred ] = MPC_yalmip( A, B, Q, R, N, kesi, state_k1, umin, umax, delta_umin, delta_umax, Ref, MPC_solver)2.定义变量
采用yalmip语言定义预测域的状态变量和控制变量,大小为3*(N+1)和2*N。
x=sdpvar(size(A,2),N+1);%维度:[x;y;phi]*(N+1)
u=sdpvar(size(B,2),N); %维度:[v;delta]*N3.约束
约束部分参照第三部分依次设置:初始条件,动力学模型约束,控制量约束,控制增量约束。动力学模型约束参照之前线性化的等式来设定,需要事先计算ξ(k+1)和A、B矩阵。
采用yalmip语言,可以通过for循环、==、<=设定约束,极为便利,不需要去推导庞大的约束矩阵。
Constraints = [ x(:,1)==kesi(1:3)]; %初始条件
for i = 1:N
Constraints=[Constraints;
%运动学模型约束
x(:,i+1) == A*(x(:,i)-kesi(1:3)) + B*(u(:,i)-kesi(4:5))+state_k1;%非线性
umin<=u(:,i)<=umax;%控制量约束
];
end
for i = 1:N-1
Constraints=[Constraints;
%控制增量约束
delta_umin<=u(:,1)-kesi(4:5)<=delta_umax;
delta_umin<=u(:,i)-u(:,i+1) <=delta_umax;
];
end 4.成本函数
同样通过for循环设置成本函数。
Cost=0;
for i=1:N
Cost=Cost+(x(:,i+1)-Ref(:,i))'*Q*(x(:,i+1)-Ref(:,i));
end
for i=1:N
Cost=Cost+u(:,i)'*R*u(:,i);
end 5.求解
使用yalmip语言调用求解器进行求解,最后输出所需的控制量。
options = sdpsettings('verbose',1,'solver', MPC_solver);
Problem = optimize(Constraints,Cost,options);
uPred = double( u(:,1));整个MPC函数如下:
function [ x, uPred ] = MPC_yalmip( A, B, Q, R, N, kesi, state_k1, umin, umax, delta_umin, delta_umax, Ref, MPC_solver)
yalmip('clear');%清理内存
% ===== 定义变量 =====
x=sdpvar(size(A,2),N+1);%维度:[x;y;phi]*(N+1)
u=sdpvar(size(B,2),N); %维度:[v;delta]*N
% ===== 设置约束 =====
Constraints = [ x(:,1)==kesi(1:3)]; %初始条件
for i = 1:N
Constraints=[Constraints;
%运动学模型约束
x(:,i+1) == A*(x(:,i)-kesi(1:3)) + B*(u(:,i)-kesi(4:5))+state_k1;%非线性
umin<=u(:,i)<=umax;%控制量约束
];
end
for i = 1:N-1
Constraints=[Constraints;
%控制增量约束
delta_umin<=u(:,1)-kesi(4:5)<=delta_umax;
delta_umin<=u(:,i)-u(:,i+1) <=delta_umax;
];
end
% ===== 定义成本函数 =====
Cost=0;
for i=1:N
Cost=Cost+(x(:,i+1)-Ref(:,i))'*Q*(x(:,i+1)-Ref(:,i));
end
for i=1:N
Cost=Cost+u(:,i)'*R*u(:,i);
end
% ===== 求解 =====
options = sdpsettings('verbose',1,'solver', MPC_solver);
Problem = optimize(Constraints,Cost,options);
uPred = double( u(:,1));
end6.完整代码
完整代码是对圆形轨迹进行跟踪,对被控车辆部分进行了简化,安装yalmip后可直接运行。
主函数部分先设定了车辆初始状态,然后调用子函数mdlOutputs(对应S函数的mdlOutputs部分)进行轨迹跟踪,mdlOutputs内部计算各矩阵之后,调用MPC_yalmip函数进行优化求解。mdlOutputs的输出会输入给被控车辆(这里使用离散化模型代替Carsim车辆),之后通过输入更新车辆状态,最后绘制x,y,phi的跟踪结果。
clear;clc;
%% 主函数
% ===== 参数 =====
global U T
T=0.05;%离散时间
L=2.6;%轴距
T_all=30;%总时间
% ===== 初始化 =====
x0=0;
y0=10;%10
phi0=0;
v0=5;
delta0=0;
U=[v0;delta0];
% ===== 运行模型 =====
kesi_cell=cell(1,T_all/T+1);%状态量和控制量矩阵
i=1;
kesi_cell{i}=[x0;y0;phi0;v0;delta0];
for t=0:T:T_all
state_t=kesi_cell{i}(1:3);
x=state_t(1);%横坐标
y=state_t(2);%纵坐标
phi=state_t(3);%航向角
sys = mdlOutputs(t,1,state_t);%MPC计算
v=sys(1); %车速
delta=sys(2); %前轮转角
%被控车辆:以离散化的运动学模型代替
i=i+1;
state_k=[v*cos(phi);v*sin(phi);v*tan(delta)/L]*T+[x;y;phi];
kesi_cell{i}=[state_k;sys];%存储状态量和控制量
fprintf('时间:%.2fs\n',t);
end
kesi=cell2mat(kesi_cell);%状态量矩阵[x;y;phi]
%% ===== 绘图 =====
figure;
subplot(1,2,1)
hold on;
plot(kesi(1,:),kesi(2,:),'-*');%绘制x,y坐标
tt=0:T:40;
x_ref=25*sin(0.2*tt);
y_ref=25+10-25*cos(0.2*tt);
plot(x_ref,y_ref,'r');
xlabel('x/m');
ylabel('y/m');
legend('实际轨迹','参考轨迹')
subplot(1,2,2);
hold on;
plot(0:T:T_all+T,kesi(3,:),'-*');
phi_ref=0.2*tt;
plot(tt,phi_ref,'r');
xlabel('t/s');
ylabel('phi');
legend('实际轨迹','参考轨迹')
%% ===== 子函数 =====
%% 模型计算输出
function sys = mdlOutputs(t,~,u)
% ===== 车辆参数及输入 =====
global U T %控制量 离散时间
N=25;%控制步长
L=2.6;%轴距
%当前状态量:S函数输入为u
x=u(1);%横坐标
y=u(2);%纵坐标
phi=u(3);%航向角
%控制量
v=U(1); %车速
delta=U(2); %前轮转角
kesi=[x,y,phi,v,delta]';
%下一时刻状态量
state_k1=[v*cos(phi);v*sin(phi);v*tan(delta)/L]*T+[x;y;phi];
% ===== 参考轨迹 =====
%圆形轨迹
Q=diag([100 100 10])*1;
R=diag([1 1])*10;%控制增量(Nu,Nu)
Ref_cell=cell(1,N);
for p=1:1:N
x_ref=25*sin(0.2*(T*p+t));
y_ref=25+10-25*cos(0.2*(T*p+t));
phi_ref=0.2*(T*p+t);
% v_ref=5;
% delta_ref=0.104;
Ref_cell{1,p}=[x_ref;y_ref;phi_ref];
end
Ref=cell2mat(Ref_cell);
% ===== 求解器 =====
MPC_solver = 'gurobi'; % 'gurobi' or 'quadprog'.
% ===== 系统矩阵A,B =====
A=[ 1, 0, -T*v*sin(phi);
0, 1, T*v*cos(phi);
0, 0, 1];
B=[ T*cos(phi), 0;
T*sin(phi), 0;
0, T*v/cos(delta)^2 /L ];
% ===== 构建约束矩阵 =====
%控制量约束
umin=[4.8;-0.436];%-0.2五、结果
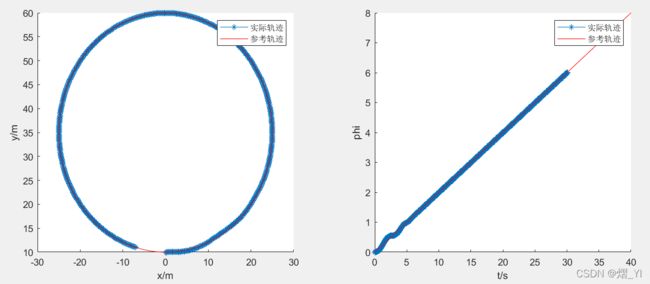
以下为MPC对圆形轨迹跟踪的结果,x,y坐标、航向角的实际轨迹和参考轨迹对比
第一组:初始位置(0,10)
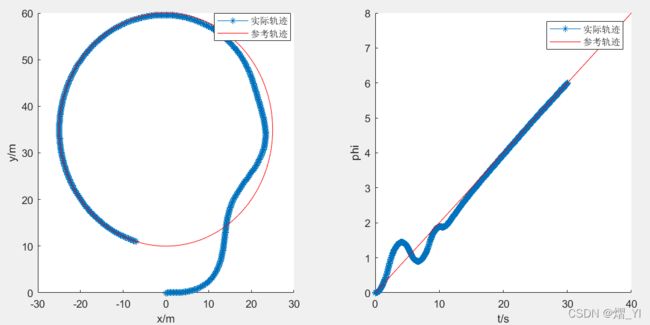
第二组:初始位置(0,0)
参数设置:x0=0; y0=0; N=80;
( 第二组初始跟踪效果比较一般,有待改善。)
总结
1.本文采用yalmip编写无人驾驶车辆MPC代码,简化了庞大的状态量、控制量矩阵以及约束矩阵的推导计算过程,代码与对应的优化问题更便于理解,修改时不易出现维度不同引起的错误。
2.所编写的代码对标《无人驾驶车辆模型预测控制》(第二版)第四章的代码,mdlOutputs函数可替换S函数相应的mdlOutputs,适当修改可以实现Carsim和Simulink联合仿真。使用此代码需要学习yalmip语言,并大概了解《无人驾驶车辆模型预测控制》书中的代码。
3.采用yalmip工具的优势在于简化代码,相应的代价则是降低了计算效率。与直接使用求解器(如quadprog)相比,计算效率仅为1/10左右。
4.个人认为在编写复杂MPC代码时,使用yalmip工具能节省大量时间,减少代码出错的概率。此外,yalmip也便于随时更换求解器和设置非线性约束。