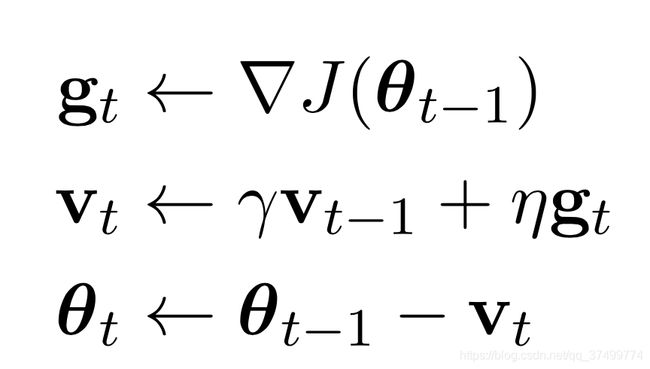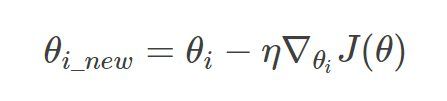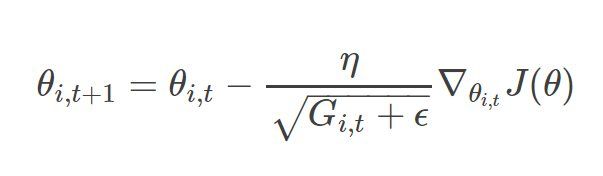机器学习&深度学习相关面试

机器学习基础知识

前人的肩膀

寿安的csdn整理

L1L2正则

判别式模型（Discriminative Model）是直接对条件概率p(y|x;θ)建模。常见的判别式模型有 线性回归模型、线性判别分析、支持向量机SVM、神经网络等。

生成式模型（Generative Model）则会对x和y的联合分布p(x,y)建模，然后通过贝叶斯公式来求得p(yi|x)，然后选取使得p(yi|x)最大的yi，
常见的生成式模型有 隐马尔可夫模型HMM、朴素贝叶斯模型、高斯混合模型GMM、LDA等。

求precision和recall

列出混淆矩阵先

AUC

AUC是一种衡量机器学习模型分类性能的重要且非常常用的指标,其只能用于二分类的情况.
AUC的本质含义反映的是对于任意一对正负例样本,模型将正样本预测为正例的可能性 大于 将负例预测为正例的可能性的 概率( 没办法这句话就是这么绕, rap~).

FPR和TPR分别是ROC曲线的横坐标和纵坐标

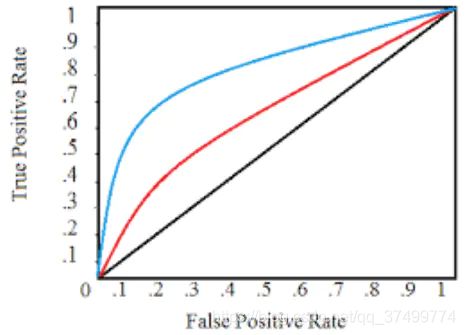
此外,对于图ROC curve中的三根曲线的理解:

• 黑线: 几何含义即ROC图的对角线, 数值含义即TPR = FPR,物理含义即对于任意抽取的样本,模型将其中正例预测为正例的概率和将负例预测为正例的概率是相等的.这也就意味着和随机分类的性能一样.
• 红蓝色线: 通常来讲, 我们的机器学习模型要优于随机分类器,因此我们经常看到的曲线往往都是像蓝色线和红色线一样的ROC曲线.它们相比黑线是有明显上凸的,同样的横坐标(FPR)下,红蓝线纵坐标(TPR)是大于黑线的,即代表模型将正例预测为正例的概率要大于将负例预测为正例的概率.同理可以看出蓝线模型由于红线模型.

AUC即ROC曲线下方与坐标轴围成的面积大小。AUC更直观地反应了ROC曲线向我们表达的模型分类能力.其数值大小(越大越好)代表了模型的性能优劣.说到这里,自然也就能够明白开篇关于AUC物理意义的阐述了,重申一遍即:AUC的本质含义反映的是对于任意一对正负例样本,模型将正样本预测为正例的可能性 大于 将负例预测为正例的可能性的 概率(例如: 当AUC = 0.5, ROC曲线为黑线时, 模型将一对正负例样本中的正样本预测为正例的概率为0.5,将负样本预测为正例的概率也为0.5,等效于随机分类预测).

解释梯度的概念

梯度的提出是为回答一个问题：
函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？

梯度定义如下：
函数在某一点的梯度是一个向量，它的方向与取得最大方向导数（因为方向导数不止一个）的方向一致，而它的模为方向导数的最大值。

SGD, Momentum, Adagrad,RMSProp, Adam原理

深度学习最全优化方法总结比较
通俗理解Adam Optimizer
这部分还是得要再好好复习复习，具体公式记住的前提下，进行灵活记忆

1. SGD为随机梯度下降，每一次迭代计算数据集的mini-batch的梯度，然后对参数进行更新
2. Momentum参考了物理中动量的概念，前几次的梯度也会参与到当前的计算中，但是前几轮的梯度叠加在当前计算中会有一定的衰减。
3. Adagrad在训练的过程中可以自动变更学习的速率，设置一个全局的学习率，而实际的学习率与以往的参数模和的平方成反比。
4. RMSProp的核心: 使用指数衰减滑动平均以丢弃遥远过去的历史。
5. Adam算法核心是RMSProp思想+Momentum思想，不仅可以独立地适应适应所有模型参数的学习率，而且可以使用指数加权平均数来计算梯度变化的方向。

另一种解释如下：
SGD
（1）初始化参数
（2）计算每个参数处的梯度
（3）更新参数
（4）重复步骤2和3，直到代价值稳定
在实际应用中，使用小批量进行参数更新的mini-batch gradient descent也常常被叫做SGD，一般我们对使用单个训练数据更新还是小批量更新不做过分区分，而主要关注算法本身。

基于动量的梯度下降法。
g_t是梯度值，v_t表示了动量的累加。特点：

• 下降初期，使用上一次参数更新，下降方向一致，乘上较大的能够进行很好的加速。
• 下降中后期时，在局部最小值来回振荡的时候，使得更新幅度增大，跳出陷阱。
• 在梯度改变方向的时候，能够减少更新，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛。
  参考链接

Adagrad（不好走路的鞋子）
在基本的梯度下降优化中，有一个常见的问题是，要优化的变量对于目标函数的依赖是各不相同的。对于某些变量，已经优化到了极小值附近，但是有的变量仍然在梯度很大的地方，这时候一个统一的全局学习率是可能出现问题的。如果学习率太小，则梯度很大的变量会收敛很慢，如果学习率太大，已经趋向于收敛的变量可能会不稳定。

Adagrad是一种基于梯度的优化算法：自适应学习率，其基本思想是对每个变量用不同的学习率，这个学习率在一开始比较大，用于快速梯度下降。随着优化过程的进行，对于已经下降很多的变量，则减缓学习率，对于还没怎么下降的变量，则保持一个较大的学习率：

t代表每一次迭代。ϵ一般是一个极小值，防止分母为0。G_i,t表示了前t步参数梯度的平方累加。把沿路的Gradient的平方根，作为正则化项。分母作为正则化项的工作机制如下：

• 训练前期，梯度较小，使得正则化项很大，放大梯度（激励阶段）
• 训练后期，梯度较大，使得正则化项很小，缩小梯度（惩罚阶段）
  简单来说，对错误的方向，有了新的阻力

Adadelta
Adadelta优化器是Adagrad的延伸，试图减少其过激的、单调降低的学习率。Adadelta不积累所有过去的平方梯度，而是将积累的过去梯度的窗口限制在一定的大小。
针对梯度下降算法提出了一种新型的适用于高维情况下学习率设置方法，称为AdaDelta。这种方法仅仅使用一阶导数信息，具有良好的动态适应性，并且与原始随机梯度下降算法相比具有更小的计算开销。这种方法不需要人工调节学习率而且对噪声梯度信息、不同模型结构、不同的数据模式以及超参数的选择表现出较强的鲁棒性。

RMSprop
适应性学习率方法，解决Adagrad激进的学习率缩减问题，修改AdaGrad以在非凸情况下表现更好，它改变梯度累积为指针加权的移动平均值，从而丢弃距离较远的历史梯度信息。

Adam
这个方法不仅存储了AdaDelta先前平方梯度的指数衰减平均值，而且保持了先前梯度M(t)的指数衰减平均值，这一点与动量类似，并对Adam进行拓展提出Adamax对学习率的上限提供了一个更简单的范围。
参考链接
缺点：
Adam算法并不能保证找到极值点。其次，Adam算法在收敛到一个次优解时，观察到一些小批次样本贡献了大幅且有效的信息梯度，指数平均后减小了它们的影响，导致模型收敛性差。

优化算法的常用tricks

https://zhuanlan.zhihu.com/p/32338983
https://www.cnblogs.com/guoyaohua/p/8542554.html
https://mofanpy.com/tutorials/machine-learning/torch/intro-speed-up-learning/
https://www.jianshu.com/p/e344981baf45
https://www.cnblogs.com/guoyaohua/p/8542554.html
https://mofanpy.com/tutorials/machine-learning/tensorflow/optimizer/

L1不可导的时候该怎么办

当损失函数不可导,梯度下降不再有效,可以使用坐标轴下降法,梯度下降是沿着当前点的负梯度方向进行参数更新,而坐标轴下降法是沿着坐标轴的方向,假设有m个特征个数,坐标轴下降法进参数更新的时候,先固定m-1个值,然后再求另外一个的局部最优解,从而避免损失函数不可导问题。

为什么L1和L2正则化可防止过拟合

1、优化角度分析
2、梯度角度分析
3、先验概率角度分析
4、知乎点赞最多的图形角度分析
5、限制条件角度分析
6、PRML的图形角度分析

https://zhuanlan.zhihu.com/p/85630046

PCA

PCA是比较常见的线性降维方法，通过线性投影将高维数据映射到低维数据中，所期望的是在投影的维度上，新特征自身的方差尽量大，方差越大特征越有效，尽量使产生的新特征间的相关性越小。
PCA算法的具体操作为对所有的样本进行中心化操作，计算样本的协方差矩阵，然后对协方差矩阵做特征值分解，取最大的n个特征值对应的特征向量构造投影矩阵。

https://zhuanlan.zhihu.com/p/77151308

拟牛顿法的原理

通俗来说梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。
在牛顿法的迭代中，需要计算海森矩阵的逆矩阵，这一计算比较复杂，考虑引入了Hessian矩阵的近似矩阵,避免了每次都计算Hessian矩阵的逆,在拟牛顿法中,用Hessian矩阵的逆矩阵来代替Hessian矩阵,虽然不能像牛顿法那样保证最优化的方向,但其逆矩阵始终是正定的,因此算法始终朝最优化的方向搜索。

处理分类问题常用算法

交叉熵公式

LR公式，LR的推导、损失函数

M为样本个数,为模型对样本i的预测结果,yi为样本i的真实标签。

逻辑回归多分类实现

SVM什么时候用线性核，什么时候使用高斯核

支持向量机为一个二分类模型,它的基本模型定义为特征空间上的间隔最大的线性分类器。而它的学习策略为最大化分类间隔,最终可转化为凸二次规划问题求解。
当数据的特征提取的较好,所包含的信息量足够大,很多问题是线性可分的那么可以采用线性核。若特征数较少,样本数适中,对于时间不敏感,遇到的问题是线性不可分的时候可以使用高斯核来达到更好的效果。

比较LR和GBDT，说说什么情景下GBDT不如LR

先说说LR和GBDT的区别：

• LR是线性模型，可解释性强，很容易并行化，但学习能力有限，需要大量的人工特征工程
• GBDT是非线性模型，具有天然的特征组合优势，特征表达能力强，但是树与树之间无法并行训练，而且树模型很容易过拟合

在高维稀疏特征的场景下，LR的效果一般会比GBDT好。

因为现在的模型普遍都会带着正则项，而 LR 等线性模型的正则项是对权重的惩罚，也就是 W1一旦过大，惩罚就会很大，进一步压缩 W1的值，使他不至于过大。但是，树模型则不一样，树模型的惩罚项通常为叶子节点数和深度等，而我们都知道，对于上面这种情况，树只需要一个节点就可以完美分割9990和10个样本，一个结点，最终产生的惩罚项极其之小。

这也就是为什么在高维稀疏特征的时候，线性模型会比非线性模型好的原因了：带正则化的线性模型比较不容易对稀疏特征过拟合。

逻辑回归的常见面试点总结

https://www.cnblogs.com/modifyrong/p/7739955.html

一句话概括：逻辑回归假设数据服从伯努利分布，通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

1. 逻辑回归的假设

2. 逻辑回归的损失函数
   逻辑回归的损失函数是它的极大似然函数

3. 逻辑回归的求解方法
   由于该极大似然函数无法直接求解，我们一般通过对该函数进行梯度下降来不断逼近最优解。在这个地方其实会有个加分项，考察你对其他优化方法的理解。因为梯度下降本身来看的话，就有随机梯度下降，批梯度下降，small batch梯度下降三种方式

4. 逻辑回归的目的
   二分类

5. 逻辑回归如何分类
   逻辑回归作为一种“回归”，y值是一个连续的变量，逻辑回归的做法是划定一个阈值，y值大于一定阈值的是一类，小于的是另一类。

6. 逻辑回归的损失函数为什么要使用极大似然函数？
   损失函数一般有四种常用，平方损失、对数损失、HingeLoss0-1损失，绝对值损失。
   将极大似然函数取对数之后等同于对数损失函数。在逻辑回归模型下，对数损失函数的训练求解速度比较快。
   
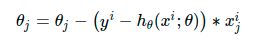
   这个式子的更新速度只和xij，yi相关。和sigmod函数本身的梯度是无关的。这样更新的速度是可以自始至终都比较的稳定。

如果你使用平方损失函数，你会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢

逻辑回归本身无法筛选特征。有时候，我们会用gbdt来筛选特征，然后再上逻辑回归

Kmeans算法和EM算法的关系

K-means的算法步骤里我们可以看出它其实就是EM的体现
手肘法

说说常见的优化器以及优化思路，写出他们的优化公式

梯度消失的根本原因（初始化和Normalization两个角度）
为什么GCN难以训练
笔者从Over smoothing，梯度消失等方面回

介绍GBDT的详细计算过程

问了xgboost缺失值处理方法

为什么xgboost要二阶展开？

除了梯度下降，你还了解哪些优化方法

数据怎么清洗，缺失值怎么填充

集成学习的方法有哪些

Relu和PRelu和Relu6和LeakyRelu区别

Parameter relu，可学习参数
relu6，人为截断，6是个阈值

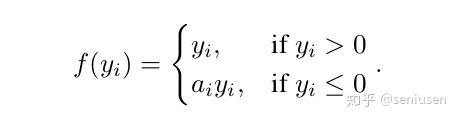
其中，yi是非线性激活函数f在第i个通道的输入，ai负责控制负半轴的斜率。在这里，我们允许不同通道的激活函数不一样。当ai是一个可以学习的参数。

如果ai是一个小的固定值，那么ai就变成了LRelu(Leaky ReLU)。LRelu的动机是为了避免零梯度，但是，作者希望模型能够自适应地学习[公式]的参数，从而能够得到更专门的激活函数。

介绍一下随机森林，都有哪些参数，随机森林如何处理缺失值

bagging + 决策树 = 随机森林。这是在共拥有m个特征的决策树中随机选择k个特征组成n棵决策树，再选择预测结果模式。步骤如下：

1. 预设模型的超参数，比如森林中有多少树 （Num of Learners）,每棵树最多几层深度（Max Depth）等。

2. 训练每个决策树，我们从完整的数据集(N 个样本，D个feature）中随机采样，选取n个样本，d 个feature，从而保证每个决策树看问题的角度都不一样。然后根据每次采样，训练一个决策树。

3. 当每个决策树都完成了训练，输入待测样本集（Test Set），我们再把最后每个树的测试结果整合在一起。对于regression问题，我们通常采用均值的方法将所有结果整合；对于classification问题，我们通常采用mode，即找到所有输出中最多的类别当做最终的输出。

优缺点：
cons：
1. 模型随机性强（随机采取样本，每个样本的特征也随机），不容易overfit，并且对于噪音点或者异常点outlier也不是那么敏感。
2. 由于每次采样只选取原数据集中一部分，因此处理高维数据相对更快
3. 树状结构，模型可解释度高。

pros: 由于这类算法不专注于解决困难样本，所以模型的性能往往受限。

随机森林可以并行计算吗？

可以

介绍一下XGBoost，都有哪些参数，如何处理缺失值

参考链接

如何处理缺失值

• 在寻找split point的时候，不会对该特征为missing的样本进行遍历统计，只对该列特征值为non-missing的样本上对应的特征值进行遍历，通过这个技巧来减少了为稀疏离散特征寻找split point的时间开销。
• 在逻辑实现上，为了保证完备性，会分别处理将missing该特征值的样本分配到左叶子结点和右叶子结点的两种情形，计算增益后选择增益大的方向进行分裂即可。
• 如果在训练中没有缺失值而在预测中出现缺失，那么会自动将缺失值的划分方向放到右子树。

区分Adaboost、GBDT、XGBoost

1. Adaboost强调Adaptive（自适应），通过不断修改样本权重（增大分错样本权重，降低分对样本权重），不断加入弱分类器进行boosting。
2. GBDT则是旨在不断减少残差（回归），通过不断加入新的树旨在在残差减少（负梯度）的方向上建立一个新的模型。——即损失函数是旨在最快速度降低残差。
3. 而XGBoost的boosting策略则与GBDT类似，区别在于GBDT旨在通过不断加入新的树最快速度降低残差，而XGBoost则可以人为定义损失函数（可以是最小平方差、logistic loss function、hinge loss function或者人为定义的loss function），只需要知道该loss function对参数的一阶、二阶导数便可以进行boosting，其进一步增大了模型的泛华能力，其贪婪法寻找添加树的结构以及loss function中的损失函数与正则项等一系列策略也使得XGBoost预测更准确。
   GBDT与XGBoost的区别

深度学习基础知识

计算题

1. 感受野的计算

2. 参数量的计算
   parameter = (k_w x k_h x C_in + 1) x C_out
   k_w x k_h x C_in 表示一个卷积核的权重数量，+1表示偏置，乘以C_out表示该层有C_out个卷积核
   注意：参数量跟feature map的尺寸大小无关！

3. 计算量的计算——FLOPs（Floating Point Operations）浮点运算次数，用来衡量算法的时间复杂度

   • 卷积层的FLOPs = [(C_in x k_w x k_h) + (C_in x k_w x h_h - 1) + 1] x C_out x w_out x h_out
     k_w和k_h分别表示卷积核的宽和高，其中C_in x k_w x k_h表示乘法计算量，C_in x k_w x k_h - 1表示加法计算量（因为加号要放在式子的每两项之间，所以-1），+1表示偏置，C_out x w_out x h_out表示输出层feature map中的所有元素，w，h表示输出层feature map的宽和高。
   • 全连接层的FLOPs = [In + (In - 1) + 1] x Out。
     In和Out 分别表示输入的特征数和输出的特征数。
     其中 In 表示乘法运算量， In - 1 表示加法运算量，+1表示偏置

4. 计算卷积层后的图像尺寸
   设输入图像尺寸：WW
   卷积核尺寸： KK
   stride：S
   padding：P
   输出尺寸：output_size = (W - K + 2P) / S + 1

5. FLOPS的计算
   FLOPs意为每秒浮点运算次数，计算乘加操作
   FLOPS（Floating Point Operations per Seconds）意为时间浮点运算次数，用来衡量硬件计算性能。

参考链接1
参考链接2

平移不变性

不变性意味着即使目标的外观发生了某种变化，但是你依然可以把它识别出来。这对图像分类来说是一种很好的特性，因为我们希望图像中目标无论是被平移，被旋转，还是被缩放，甚至是不同的光照条件、视角，都可以被成功地识别出来。

复现一下NMS

根据候选框的类别分类概率做排序：A < B < C < E < F

1. 先标记最大概率矩形框F是我们要保留下来的；
2. 从最大概率矩形框F开始，分别判断A~E与F的重叠度IOU（两框的交并比）是否大于某个设定的预制，假设B，D与F的重叠度超过阈值，那么就扔掉B，D
3. 从剩下的矩形框A、C、E中，选择概率最大的E，标记为要保留下来的，然后判断E与A、C的重叠度，扔掉重叠度超过设定阈值的矩形框
4. 直到剩下的矩形框没有了，标记完所有要保留下来的矩形框。
   参考链接

为什么要学习偏移而不是实际值？

1、Anchor已经粗略地“框住了”输入图像中的目标，明显的一个问题是，框的不够准确。因为受限于anchor的生成方式，anchor的坐标永远都是固定的那几个。
所以，如果我们需要预测相对于anchor的offset，那么，就可以通过预测的offset调整anchor位置，从而得到更准的bounding box。

2、理论上，如果CNN接收同一类型的物体两次，那么不管CNN在图像中的哪个位置接收到物体，CNN都应该输出大致相同的值两次。

这意味着，如果一幅图像包含两辆车，而输出结果是绝对坐标，那么网络将预测两辆车大致相同的坐标。

而学习anchor偏移，允许这两辆车具有相似偏移输出，但偏移应用于锚定，锚定可映射到输入图像中的不同位置。这是在anchor回归过程中学习锚定盒偏移的主要原因。

3、为什么要学习偏移系数而不是偏移量？
首先，对于预测的bounding box的w和h可以通过anchor进行缩放，但有一个基本的要求，就是h和w都必须为正值，而网络最后一层的预测输出是没法保证正负的，所以最简单的方法就是对预测输出求exp，这样就保证了预测值恒为正。那么反过来，对预测目标就是求log。

其次，对cx和cy除以anchor的宽和高的处理是为了做尺度归一化。例如，大的box的绝对偏移量一般较大，而小的box的绝对偏移量一般较小，除以宽和高消除这种影响。即两个框大小不一，但相对值却一致。

Yolo系列面经

链接

1. 为什么类别预测方面，使用独立的逻辑回归分类器而不是softmax？
   答：类别预测方面使用多标签分类而非单标签分类，使用独立的逻辑回归分类器(logistic classifier)取代softmax。我想这应该也是多标签分类的需要，使用softmax的话得到的是属于某一类的概率，而一个预测框中经常有多个类别。使用逻辑回归可以针对每一个类别使用一个分类器，当大于某个阈值的时候则认为存在訪类别。训练过程中类别损失函数使用二分类交叉熵损失。

2. 介绍一下yolov3目标评分如何实现？
   答：YOLOv3使用逻辑回归来预测bounding box的目标评分（objectness score）。具体如下：当某个先验框（bounding box prior也就是生成的9个anchor）与ground truth的IOU大于其他所有先验框时，目标评分为1。如果一个先验框和某个ground truth的IoU虽然不是最大的那个，但是IoU也大于了某个阈值，我们仍然会忽略这个先验框（既不惩罚，也不奖励），这个借鉴了Faster RCNN（对于每个滑窗, 会生成 9 个 anchors）。对于每个ground truth只分配给IoU最好的那个先验框。如果一个先验框没有分配给任何一个ground truth，那么訪框没有坐标和分类上的损失，我们只考虑它目标评分的损失，即试图减小其objectness score。

   logistic回归就是用来从9个anchor priors中找到objectness score(目标存在可能性得分)最高的那一个。logistic回归就是用曲线对prior相对于 objectness score映射关系的线性建模。
   σ()函数为logistic函数，将坐标归一化到0-1之间。最终得到的bx,by为归一化后的相对于grid cell的值
   σ(t0)表示预测的边框的置信度，为预测的边框的概率和预测的边框与ground truth的IOU值的乘积。

3. 如何理解多尺度
   首先，借鉴了SPP

其次，在yolov3中，最终有3个分支输出做预测，输出的特征图大小分别为1313，2626，52*52，每个特征图使用3个anchor，

13*13的特征图使用(116 × 90); (156 × 198); (373 × 326);这3个anchor

26*26的特征图使用(30× 61); (62× 45); (59×119);这3个anchor

52*52的特征图使用(10× 13); (16× 30); (33× 23);这3个anchor

最后，FPN结构的输出，并没有像SSD那样直接采用backbone中间层的处理结果作为feature map的输出，而是和后面网络层的上采样结果进行一个拼接之后的处理结果作为feature map。为什么这么做呢？这是为了实现小对象检测，因为不同水平的特征图倾向于检测的对象尺寸不同，再者，shallow layer有更详细的定位，而higher layer有更强的判别性特征(分类)，所以作者才这么做的。现在主流的检测算法都是用一堆层进行多次变换得到的，只要合理即可而已！

4. loss详细理解，并代码实现
   yolo将为每张图片输出一个大小为S x S x (5B + C)的张量，比如说S = 7，也就是最后输出的feature map 7x7，20类，那么7 x 7 x (2 x 5 + 20)，其中2也是固定的，为每个格子配置2个不同大小的框。

• yolov1 loss
  
• yolo v3 loss
  
  参考链接
  参考

5. yolo在inference的时候，是如何得到的最后的目标框，请简述此过程。

参考链接

yolov5采用了BECLogits损失函数计算objectness score的损失，class probability score采用了交叉熵损失函数，bounding box采用了GIOU Loss。GIoU Loss用来计算bounding box的loss。

上面公式的意思将两个任意框A，B，我们找到一个最小的封闭形状C，让C可以把A, B包含在内，接着计算C中没有覆盖A和B的面积占总面积的比值，然后用A与B的IoU减去这个比值。与IoU类似，GIoU也可以作为一个距离，loss可以用

yolo的前向推理，主要就是讲一下，在得到conv之后的feature map之后，经过logistics，经过yolo层，通过公式计算box的xywh四个参数，因为得到是相对值，然后根据box，找到唯一的correct box之后，将框表示在原图上即可。

yolov3和yolov5差别

这一篇写的太好了

CSPNet：出发点是要提升CNN的学习能力，大致思想是减少反向传播时的梯度的重复（梯度组合更加丰富同时还能减少计算量），实现方式是通过将浅层的feature map一分为二（这个分就是CSP中的P：Partial ），一半去经历block，一半是直接concat到block的output。

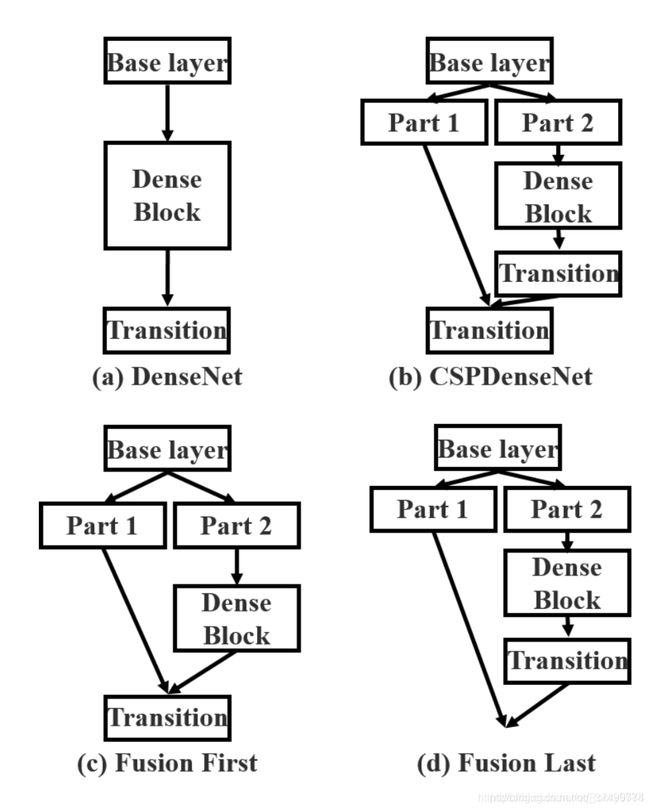
参考
PANet位在于YOLOv4模型的neck，主要通过保留空间信息来增强实例分割过程。YOLOv4中选择PANet进行实例分割的原因是它能够准确地保存空间信息，有助于正确定位像素点，形成mask。
参考

关于loss，看这个就够了

YOLO-v1

栅格系统和bounding box

假设需要被检测的类别数量为C，将原图划分为S x S的栅格（grid）

• 为每个栅格配置B个不同大小的bounding box（2个）
  • 为每个bounding box预测中心坐标(x,y)、宽度w、高度h、前景置信度conf（也就是目标都归为一类）、分类置信度
  • 注意中心坐标(x, y)是相当于栅格左上角坐标的偏移量。而在faster rcnn和ssd中，中心坐标的偏移量都是相对栅格中心的偏移！
  • 实际预测的中心坐标(x, y)、宽度w、高度h都是经过归一化的。
  • 预测阶段会计算前景置信度和分类置信度的乘积，来作为预测为该分类的得分（class-specific confidence scores）。这与Faster RCNN和SSD不同，yolo-v1没有给分类置信度留一个背景的分类，而是拆分为两个置信度来做。
  • 对于一个栅格只预测一组分类置信度，也就是说，与同一个栅格绑定的一组预测框共享一组分类置信度，也就是说，不能在一个框里面同时出现两个物体，这样就无法检测全。

YOLO-v2

yolov2指出，如果能在一开始就使用质量较高的先验框（Prior Box）会得到更好的效果，并提出用训练集上真实框和KMEANS聚类来辅助挑选先验框，这里KMEANS算法选用的距离函数为：d
针对训练集上的每个真实框，找到与之重合程度最好的先验框，计算整个训练集上的平均IOU，以此来比较不同方案下先验框的有效性。
考虑一下加入锚框anchor之后，记预测框的中心坐标为
YOLO-v2将tx、ty约束到区间(0, 1)内，即把预测框的中心坐标约束在了栅格内。

YOLO-v3

考虑到每个bounding box可能或多或少会包含其他真实框的内容（甚至真实框之间就有重叠），而使用softmax做分类会抑制其他类别的置信度，因此改为sigmoid做分类，把每个类别作为单独的二分类任务会更好些。

YOLO-v4

多尺度特征

不同尺度的感受野的意义在于，

1. 允许网络捕获各种尺度的目标
2. 允许网络捕获目标周围的上下文信息
3. 允许图像上每个点跟最终的激活值有更多的信息流通（甚至感受野超出输入图像本身）
   在多尺度特征提取上，YOLO-v4放弃了YOLOv3的FPN设计，引入了新的SPP和PANet路径集成，但预测框的生成等依旧留着YOLOv3的设计。

YOLO-v5

跟yolov4的区别
https://zhuanlan.zhihu.com/p/326284473

梯度消失和梯度爆炸

答：
梯度消失：因为通常神经网络所用的激活函数是 sigmoid 函数，这个函数有个特点，就是能将负无穷到正无穷的数映射到 0 和 1 之间，并且对这个函数求导的结果是 f′(x)=f(x)(1−f(x))。因此两个 0 到 1 之间的数相乘，得到的结果就会变得很小了。神经网络的反向传播是逐层对函数偏导相乘，因此当神经网络层数非常深的时候，最后一层产生的偏差就因为乘了很多的小于 1 的数而越来越小，最终就会变为 0，从而导致层数比较浅的权重没有更新， 这就是梯度消失。
梯度爆炸：梯度爆炸就是由于初始化权值过大，前面层会比后面层变化的更快，就会导致权值越来越大，梯度爆炸的现象就发生了。在深层网络或循环神经网络中，误差梯度可在更新中累积，变成非常大的梯度，然后导致网络权重的大幅更新，并因此使网络变得不稳定。在极端情况下，权重的值变得非常大，以至于溢出，导致 NaN 值。网络层之间的梯度（值大于 1.0）重复相乘导致的指数级增长会产生梯度爆炸。

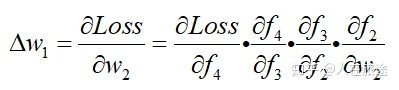
激活函数进行求导，如果此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸，如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失。

参考

一些新的目标检测的backbone有哪些，各有什么特点

https://zhuanlan.zhihu.com/p/93451942

检测里为什么选择refineDet

https://zhuanlan.zhihu.com/p/39184173

如何评价两个分布的相似度，KL散度怎么计算

https://blog.csdn.net/weixin_41396062/article/details/104623348
https://www.zhihu.com/question/39872326

YOLOV3和YOLOV2的主要区别，loss上哪里不同，smoothL1 loss的好处，Yolo里是向上取整还是向下取整

https://blog.csdn.net/qq_41736617/article/details/106583232
https://zhuanlan.zhihu.com/p/159371985

LSTM的反向传播，公式

https://zhuanlan.zhihu.com/p/83496936

Focal Loss 论文理解及公式推导

https://blog.csdn.net/zziahgf/article/details/83589973#:~:text=%E5%AF%B9%E4%BA%8EFocal%20Loss%20F%20L,)%EF%BC%8C%E5%85%B6%E4%B8%AD%20%CE%B3%20%E4%B8%BA%E5%B8%B8%E6%95%B0.

https://zhuanlan.zhihu.com/p/80594704

mean pooling和max pooling反向传播的不同

https://blog.csdn.net/Jason_yyz/article/details/80003271

Pytorch 中 Function与Module的差异与应用场景

https://blog.csdn.net/wzy_zju/article/details/81262472#:~:text=Function%E4%B8%8EModule%E9%83%BD%E5%8F%AF%E4%BB%A5,%E9%80%82%E7%94%A8%E4%BA%8E%E5%AE%9A%E4%B9%89%E4%B8%80%E4%B8%AA%E7%BD%91%E7%BB%9C

pytorch里dataset、dataloader、sampler有什么区别

https://blog.csdn.net/andyjkt/article/details/107428806

可分离卷积的思想，参数量计算

BatchNormalization的作用

神经网络在训练的时候随着网络层数的加深,激活函数的输入值的整体分布逐渐往激活函数的取值区间上下限靠近,从而导致在反向传播时低层的神经网络的梯度消失。而BatchNormalization的作用是通过规范化的手段,将越来越偏的分布拉回到标准化的分布,使得激活函数的输入值落在激活函数对输入比较敏感的区域,从而使梯度变大,加快学习收敛速度,避免梯度消失的问题。


在normalization的过程中，不可避免的会改变自身的分布，而这会导致学习到的特征的表达能力有一定程度的丢失。通过引入参数γ和β，极端情况下，网络可以将γ和β训练为原分布的标准差和均值来恢复数据的原始分布，也就是第四个线性变换。这样保证了引入BN，不会使效果更差。
参考链接

各种Norm方法

1. BN解决了ICS（Internal Covariate Shift）问题
   在BN层中，每个batch计算得到的均值和标准差是对于全局均值和标准差的近似估计，这为我们最优解的搜索引入了随机性，从而起到了正则化的作用。
2. BN的缺陷：带有BN层的网络错误率会随着batch_size的减小而迅速增大，当我们硬件条件或者别的原因导致，不得不使用较小的batch_size时，网络效果大打折扣，于是提出了LN、IN、GN方法。
3. 下图直观表达了BN LN IN GN的区别和联系：
   
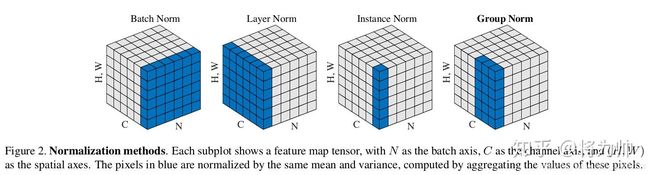
   （1）BN计算均值和标准差时，固定channel(在一个channel内)，对HW和batch作平均；
   （2）LN计算均值和标准差时，固定batch(在一个batch内)，对HW和channel作平均；
   （3）IN计算均值和标准差时，同时固定channel和batch(在一个batch内中的一个channel内)，对HW作平均；
   （4）GN计算均值和标准差时，固定batch且对channel作分组(在一个batch内对channel作分组)，在分组内对HW作平均。
   
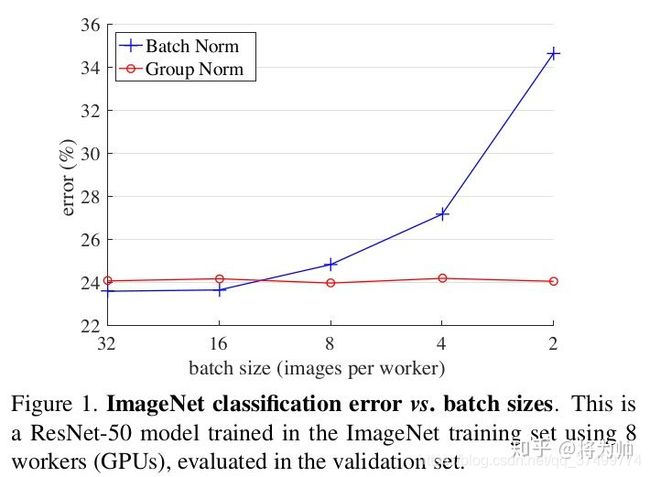
   BN和GN错误率随batch size的变化，BN的错误率随batch size的减小迅速增大，而GN的错误率基本不变

链接

循环神经网络为什么效果好

RNN是一种节点定向连接成环的人工神经网络，是一种反馈神经网络。RNN利用内部的记忆来处理任意时序的输入序列，并且在其处理单元之间既有内部的反馈连接，又有前馈连接，这使得RNN可以更加容易处理不分段的文本等。
隐藏层：其输入不仅包括输入层的输出，还包括上一时刻隐藏层的输出。网络会对之前的信息进行记忆并应用于当前的输入计算中。

LSTM和GRU的原理

Lstm由输入门，遗忘门，输出门和Cell State组成。
步骤1. 决定遗忘的记忆内容：

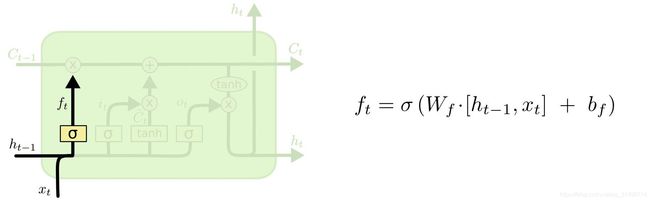
sigma使得输出ft在0~1之间。遗忘门取决于Wf权重、xt输入、和上一个时间的ht-1。
步骤2. 决定新添加的以及内容：

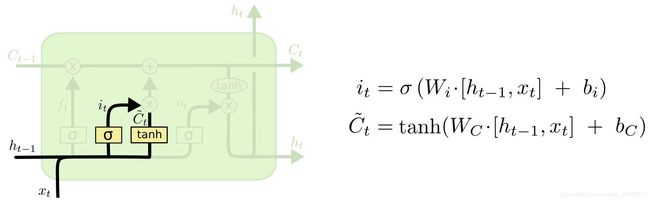
步骤3. 使用权重相加的方式更新当前记忆内容：

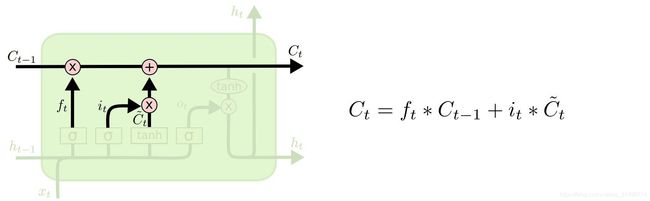
步骤4. 输出当前state

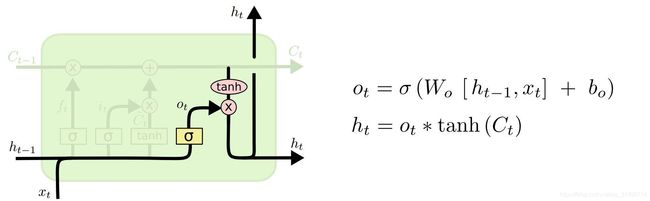
Gru由重置门和更新门组成，其输入为前一个时刻隐藏层的输出和当前的输入，输出是下一时刻隐藏层的信息。重置门用来计算候选隐藏层的输出，其作用是控制保留多少前一时刻的隐藏层。更新门的作用是控制加入多少候选隐藏层的输出信息，从而得到当前隐藏层的输出。

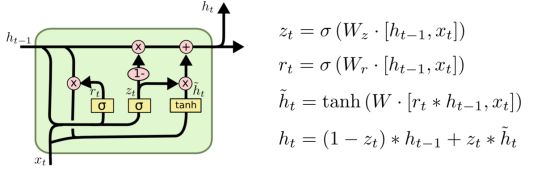
GRU和LSTM区别，就是在于门的个数不一样。

RNN由于网络较深,后面层的输出误差很难影响到前面层的计算,RNN的某一单元主要受它附近单元的影响。而LSTM因为可以通过阀门记忆一些长期的信息,相应的也就保留了更多的梯度。而GRU也可通过重置和更新两个阀门保留长期的记忆,也相对解决了梯度消失的问题。

Attention机制的作用

Attention机制其实就是一系列注意力分配系数，也就是一系列权重参数。
Seq2seq属于encoder-decoder结构的一种,利用两个RNN,一个作为encoder一个作为decoder。Encoder负责将输入序列压缩成指定长度的向量,这个向量可以看作这段序列的语义,而decoder负责根据语义向量生成指定的序列。
在Seq2Seq结构中，编码器Encoder把所有的输入序列都编码成一个统一的语义向量，然后再由解码器Decoder解码。在解码器Decoder解码的过程中，不断地将前一个时刻t-1的输出作为后一个时刻t的输入，循环解码，直到输出停止符为止。

以seq2seq中的attention公式作为讲解，Attention机制其实就是将Encoder隐藏层状态加权后获得权重向量ct，额外加入到Decoder中，给Decoder网络添加额外信息，从而给Decoder RNN加入额外信息，以提高性能。
Attention机制打破了只能利用encoder最终单一向量结果的限制，从而使模型可以集中在所有对于下一个目标单词重要的输入信息上，使模型效果得到极大的改善。

怎么提升网络的泛化能力

从数据上提升性能:收集更多的数据,对数据做缩放和变换,特征组合和重新定义问题。
从算法调优上提升性能:用可靠的模型诊断工具对模型进行诊断,权重的初始化,用小的随机数初始化权重。对学习率进行调节,尝试选择合适的激活函数,调整网络的拓扑结构,调节batch和epoch的大小,添加正则化的方法,尝试使用其它的优化方法,使用early stopping。

深度学习在语音识别中的应用

神经网络为什么用交叉熵

通过神经网络解决多分类问题时，最常用的一种方式就是在最后一层设置n个输出节点，无论在浅层神经网络还是在CNN中都是如此，比如，在AlexNet中最后的输出层有1000个节点，而即便是ResNet取消了全连接层，也会在最后有一个1000个节点的输出层。
一般情况下，最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N，那么对于每一个样例，神经网络可以得到一个N维的数组作为输出结果，数组中每一个维度会对应一个类别。在最理想的情况下，如果一个样本属于k，那么这个类别所对应的的输出节点的输出值应该为1，而其他节点的输出都为0，即[0,0,1,0,….0,0]，这个数组也就是样本的Label，是神经网络最期望的输出结果，交叉熵就是用来判定实际的输出与期望的输出的接近程度。

CycleGAN原理

CycleGAN其实就是一个A→B单向GAN加上一个B→A单向GAN。两个GAN共享两个生成器，然后各自带一个判别器，所以加起来总共有两个判别器和两个生成器。一个单向GAN有两个loss，而CycleGAN加起来总共有四个loss。CycleGAN论文的原版原理图和公式如下，其实理解了单向GAN那么CycleGAN已经很好理解。

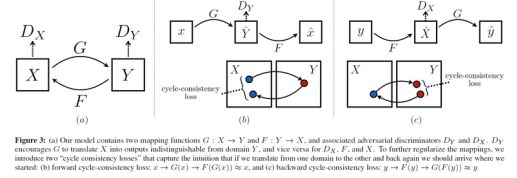
下面放一张网友们自制的CycleGAN示意图，比论文原版的更加直观，出处见水印。

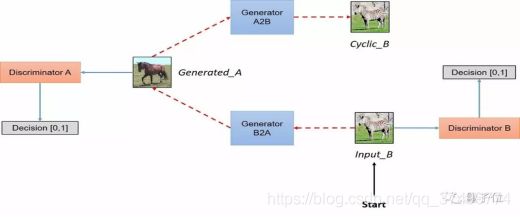
CPM 模型压缩怎么做的？有压过 OpenPose 吗？

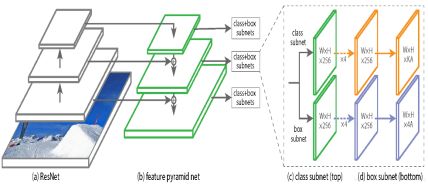
RetinaNet的大致结构

RetinaNet为什么比SSD效果好

1. RetinaNet的backbone是基于ResNet的FPN，FPN在原始的CNN基础上增加自上而下的路径和横向连接（lateral connections）
2. RetinaNet的anchor和RPN是类似的，RPN的输入特征是[公式]，每个level的特征每个位置只放置一种scale的anchor，分别为[公式]，但是却设置3中长宽比[公式]。RetinaNet的输入特征是[公式]，anchor的设置与RPN一样，但是每个位置增加3个不同的anchor大小[公式]，这样每个位置共有A=9个anchor，所有level中anchor size的最小值是32，最大值是813。
3. 检测模块主要包括分类分支和box回归分支，其中分类分支用来预测每个位置的各个anchor（数量为[公式]）的类别概率（类别数为[公式]），而box回归分支用来预测每个位置各个anchor和GT之间的offset。

谈一谈模型压缩的相关知识

三大角度：蒸馏，剪枝，量化。笔者分别介绍了三大角度的基本原理。
还有一些零碎的知识：低秩分解，ALBERT中的参数共享，深度可分离卷积，Inception V3中的大卷积核替代方案等

数据不平衡问题

笔者不光从欠采样过采样等经典解决办法的角度回答。另外回答了一些其他方法：GAN（ICCV 2019 best paper：SinGAN），特征空间增广，改进训练方式（源数据训练特征提取backbone，欠采样或过采样训练分类器），Loss加权，使用AdaGrad优化器等。

1. 数据增强
2. 权值均衡
   处理深度学习中数据集不平衡问题方法汇总

寻找最优学习率的方法（学习率从小到大观察Loss）

Warmup与优化器的搭配使用（笔者主要是谈Adam与Warmup的搭配使用，解释了Warmup的一些直觉上的理解，这个建议大家去看看知乎）

MobileNet的原理

深度可分离卷积，从参数数量以及计算量角度与传统卷积对比分析
宽度因子，分辨率因子
MobileNet与Xception以及ShuffleNet的对比

是否测试过MobileNet在不同计算设备上的运行速度？

Mobilenet v1

利用分组卷积降低网络的计算量，并且mobilenet将分组卷积应用到了极致，即网络的分组数与网络的channel数量相等，使网络的计算量减到最低，但是这样channel之间的交互就没有了，所以作者又使用的point-wise conv，即使用1*1卷积进行channel之间的融合。

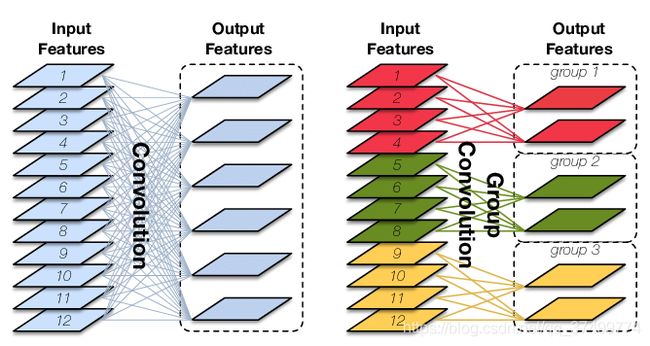
Mobilenet v2

倒残差（纺锤）

线性瓶颈

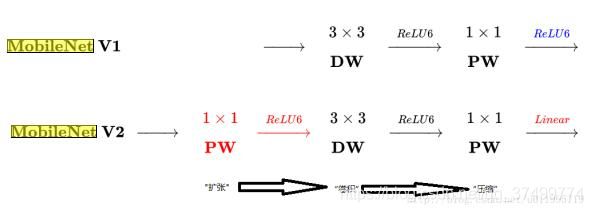
1.DWConv layer层提取得到的特征受限于输入的通道数，若是采用以往的residual block，先“压缩”，再卷积提特征，那么DWConv layer可提取得特征就太少了，因此一开始不“压缩”，MobileNetV2反其道而行，一开始先“扩张”，本文实验“扩张”倍数为6。 通常residual block里面是 “压缩”→“卷积提特征”→“扩张”，MobileNetV2就变成了 “扩张”→“卷积提特征”→ “压缩”，因此称为Inverted residuals
2.当采用“扩张”→“卷积提特征”→ “压缩”时，在“压缩”之后会碰到一个问题，那就是Relu会破坏特征。为什么这里的Relu会破坏特征呢？这得从Relu的性质说起，Relu对于负的输入，输出全为零；而本来特征就已经被“压缩”，再经过Relu的话，又要“损失”一部分特征，因此这里不采用Relu，实验结果表明这样做是正确的，这就称为Linear bottlenecks

Mobilenet v3

mobilenetv3是神经架构搜索得到的模型，其内部使用的模块继承自：
1，mobilenetv1模型引入的深度可分离卷积
2，mobilenetv2模型引入的具有线性瓶颈的倒残差结构
3，MnasNet模型引入的基于squeeze and excitation结构的轻量级注意力模型
这些被证明行之有效的用于移动端网络设计的模块是搭建mobilenetv3的积木

GhostNet

用线性变换替换一部分卷积

FPN网络主要作用（多尺度）

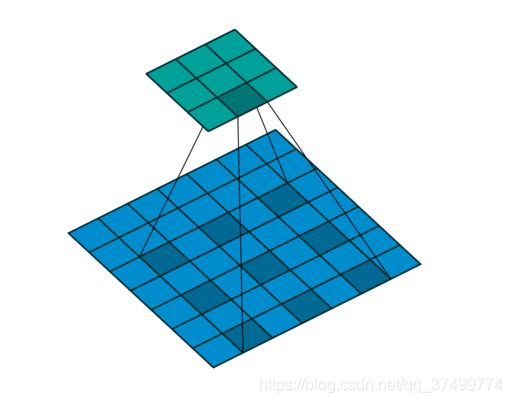
1*1卷积作用

实现跨通道的交互和信息整合,实现卷积核通道数的降维和升维,可以实现多个feature map的线性组合,而且可是实现与全连接层的等价效果。

简述一下量化操作，具体如何实现的

参考链接

AutoEncoder

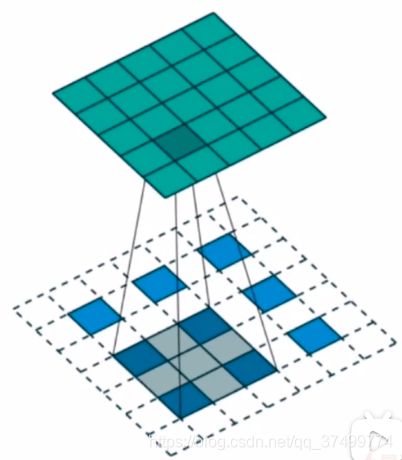
空洞卷积

在卷积核中插入空洞，起到扩大感受野的作用。

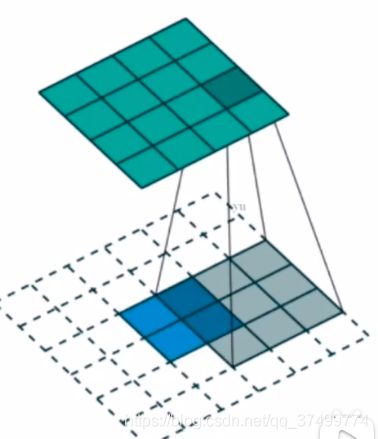
反卷积

如果将padding分布在feature map之中，就出现了Fractional strided。

IOU

各种IOU的进化版本！
https://zhuanlan.zhihu.com/p/94799295

如何解决样本不均衡问题？

数据角度

• 扩大数据集
• 数据集重采样
• 人工产生数据样本
• 基于异常检测的方式

算法层面

• 尝试不同的分类算法
• 对小类错分进行加权惩罚
• 从重构分类器的角度出发

在深度学习中，有哪些解决样本不平衡的方法？

比如扩大数据集、类别均衡采样、人工产生数据样本，添加少类别样本的来loss惩罚项等。
对于数据的方法，重点介绍：类别均衡采样。
把样本按类别分组，每个类别生成一个样本列表，训练过程中先随机选择1个或几个类别，然后从各个类别所对应的样本列表里选择随机样本。这样可以保证每个类别参与训练的机会比较均等。

梯度反向传播求根号

首先手写一下BP公式吧。
BP1：计算最后一层的反向误差
BP2：根据L + 1层的反向误差计算L层的反向误差
BP3：根据反向误差计算w的梯度
BP4：根据反向误差计算b的梯度
然后根据梯度更新参数就好了。

可以看出来，很像一个递归的过程：
第一层的反向误差需要第二层的
第二层的需要第三层的
。。。
第n-1层需要第n层的
BP1计算出第n层的反向误差
BP2就能计算所有层的反向误差
BP3和BP4就能计算参数的梯度了
这种方法也避免了计算某一层梯度时，要把后面所有层的反向误差再重新计算一遍

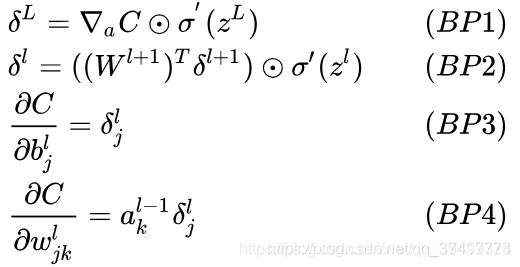
求平方根的方式有牛顿法、二分法、梯度下降法。
梯度下降法，是一个一阶最优化算法，就是让参数沿着损失函数负梯度的方向更新。迭代的步长，也就是学习率事先给定的，如果负梯度的绝对值越大，这次更新的幅度也就越大。

• 牛顿法不仅可以用来求解函数的极值问题，还可以用来求解方程的根，二者在本质上是一个问题，因为求解函数极值的思路是寻找导数为0 的点，如果要求f(x)的极值，也就是求f’(x) = 0 的根。

题目就是给定y，要求解y - x²的根，可以通过学习的方法来实现，那以x²为预测值，y为实际值，最小化损失函数 L = (y - x²) ²

这里为什么不直接用x²是因为其最小值对应的x不是我们要求的x。
构建了损失函数以后，就可以用梯度下降法来求解全局最优的x的值，即为：
g(x) = dL / dx = 4x(x² - 2)
x_n+1 = x_n - ag(x_n)
给x一个初始值，然后不断通过上式来更新x就可以逐渐逼近最优的x。

def gradient_descent(y):
    x = 1
    alpha = 0.001  # 注意学习率不能太大，否则会震荡甚至发散，啥，不信 ？！陷入死循环之后你会改回来的
    deta = 1
    while abs(deta)>0.00001:
        deta = 4*x*(x**2-y)
        x -= alpha * deta
    return x