一.冒泡排序
1.1冒泡排序引入
对于任何编程语言,当我们学到循环和数组的时候,都会介绍一种排序算法:冒泡排序;深入学习更多排序算法后和在实际使用情况中,冒泡排序的使用还是极少的。它适合数据规模很小的时候,而且它的效率也比较低,但是作为入门的排序算法,还是值得学习的。
1.2冒泡排序的核心思想与算法分析
核心思想:相邻的元素两两比较,较大的数下沉,较小的数冒起来,这样一趟比较下来,最大(小)值就会排列在一端。
因为较大的数会下沉,所以我们也可以将冒泡排序称作沉石排序。
算法分析:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个;
- 每趟从第一对相邻元素开始,对每一对相邻元素作同样的工作,直到最后一对;
- 针对所有的元素重复以上的步骤,除了已排序过的元素(每趟排序后的最后一个元素),直到没有任何一对数字需要比较。
1.3实例说明
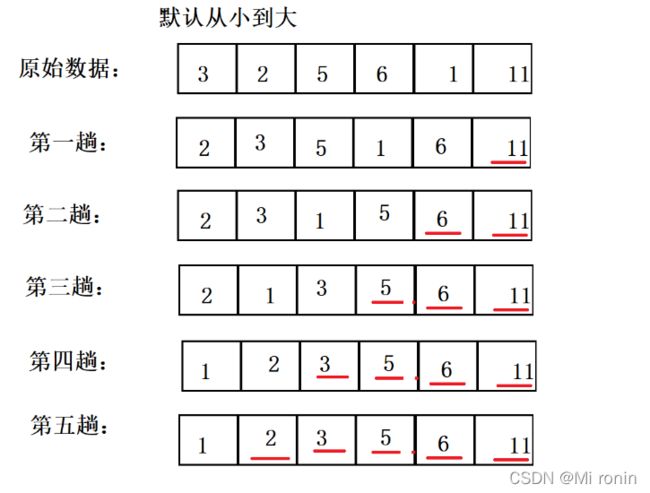
以3,2,5,6,1,11为例子,排序过程:
- 底部画线的为已确定的数据
- 有n个数据,需要跑n-1趟即可
1.4优化
上面的排序过程在第四趟处理完时,就已经完全有序了(肉眼观察的),理应直接退出循环即可,第五趟顺序完全可以省略,那么我们就会有一个问题:
怎样判断数据完全有序?
从先到后遍历一遍,发现数据两两比较都是前面小于后面(没有交换操作),这个时候,就可以判定数据已经完全有序。
1.5代码实现
void BubbleSort(int* arr, int len)
{
int count = 0;
bool tag = true;//标记 首先赋初值为真
//从头到尾遍历一般,没有交换操作,则可以认定完全有序
//反过来说:只要有一次交换操作,则不能认定完全有序
for (int i = 0; i < len - 1; i++)//需要多少趟
{
tag = true;//注意:不要忘,每一趟开始的时候,记得将tag重新置为true
for (int j = 0; j + 1 < len - i; j++)//控制两两比较 j指向两两比较的开始位置
{
if (arr[j] > arr[j + 1])
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
tag = false;
}
}
count++;
if (tag)//如果一趟跑完之后,发现tag没有变,还是真,则代表没有前面大于后面的情况发生,则已经完全有序
{
break;
}
}
printf("%d\n", count);
}
1.6性能分析
- 时间复杂度:o(n^2);
- 空间复杂度:o(1);
- 稳定性:稳定
二.堆排序
2.1堆的基础知识
2.1.1堆是什么
堆是一种数据结构,一种叫做完全二叉树的数据结构。
2.1.2堆的性质
这里我们用到两种堆,其实也算是一种。
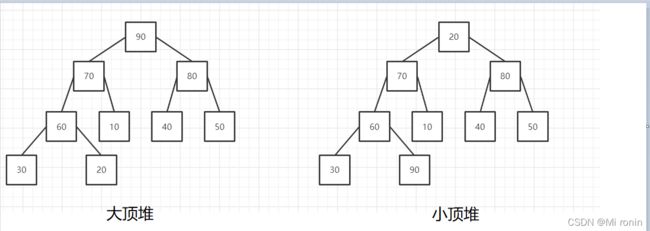
大顶堆:每个节点的值都大于或者等于它的左右子节点的值。
小顶堆:每个节点的值都小于或者等于它的左右子节点的值。
查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数,那么
1.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2*i+1
3.右孩子索引:2*i+2
如下图所示:
两种堆就是如上图所示。
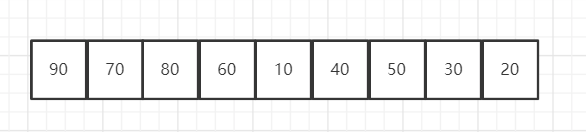
如果我们把这种逻辑结构映射到数组中,如下所示:
大顶堆:
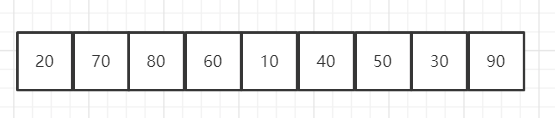
小顶堆:
从这里我们可以得出以下性质:
对于大顶堆:arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]
对于小顶堆:arr[i] <= arr[2i + 1] && arr[i] <= arr[2i + 2]
2.2堆排序的核心思想与基本步骤
核心思想:将无序数组构造成一个大顶堆,固定一个最大值,将剩余的数重新构造成一个大顶堆,重复这样的过程构造堆。
基本步骤:
- 将带排序的序列构造成一个大顶堆,根据大顶堆的性质,当前堆的根节点(堆顶)就是序列中最大的元素;
- 将堆顶元素和最后一个元素交换,然后将剩下的节点重新构造成一个大顶堆;
- 重复步骤2,如此反复,从第一次构建大顶堆开始,每一次构建,我们都能获得一个序列的最大值,然后把它放到大顶堆的尾部;
- 最后,就得到一个有序的序列了。
2.3实例说明与分析
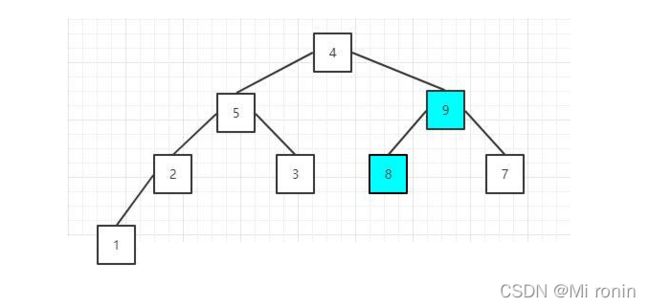
以4,5,8,2,3,9,7,1为例,按照上面的基本步骤进行排序,过程如下:
1.将无序序列构造为一个大顶堆
2.现在我们需要找到最后一个非叶子节点的位置,也就是索引值。
对于一个完全二叉树,在填满的情况下,每一层的元素个数是上一层的二倍,根节点数量是1,所以最后一层的节点数量,一定是之前所有层节点总数+1,所以,我们能找到最后一层的第一个节点的索引,即节点总数/2(根节点索引为0),这也就是第一个叶子节点,所以第一个非叶子节点的索引就是第一个叶子结点的索引-1。
那么对于填不满的二叉树呢?这个计算方式仍然适用,当我们从上往下,从左往右填充二叉树的过程中,第一个叶子节点,一定是序列长度/2,所以第一个非叶子节点的索引就是(数组长度/ 2 -1)。
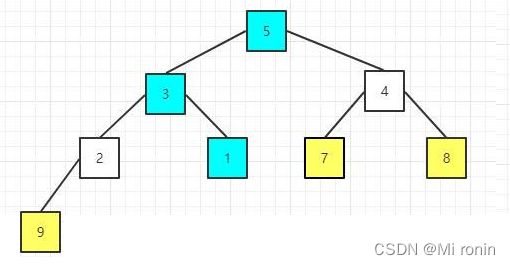
现在找到了最后一个非叶子节点,即元素值为2的节点,比较它的左右节点的值,是否比他大,如果大就换位置。这里因为1<2,所以,不需要任何操作,继续比较下一个,即元素值为8的节点,它的左节点值为9比它本身大,所以交换。
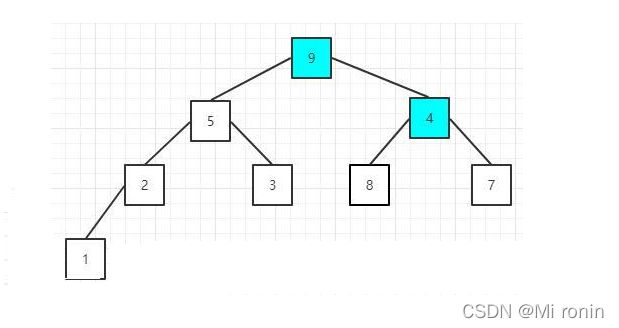
3.因为元素8没有子节点,所以继续比较下一个非叶子节点,元素值为5的节点,它的两个子节点值都比本身小,不需要调整;然后是元素值为4的节点,也就是根节点,因为9>4,所以需要调整位置
4.原来元素值为9的节点值变成4了,而且它本身有两个子节点,所以,这时需要再次调整该节点
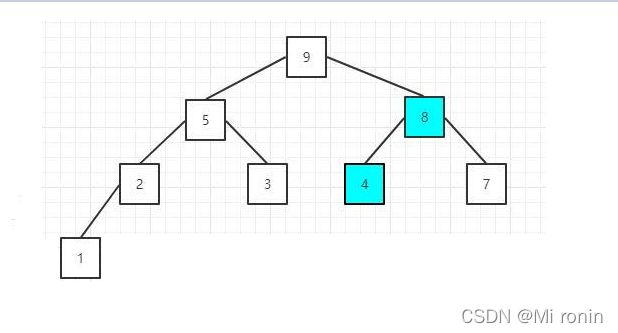
5.排序序列,将堆顶的元素值和尾部的元素交换
6.将剩余的元素重新构建大顶堆,其实就是调整根节点以及其调整后影响的子节点,因为其他节点之前已经满足大顶堆性质
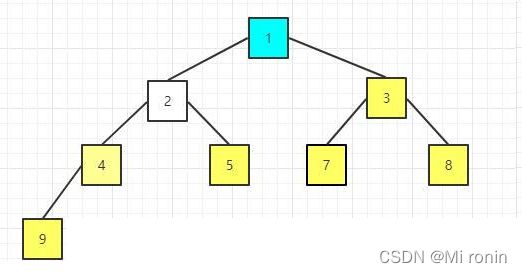
7.继续交换,堆顶节点元素值为8与当前尾部节点元素值为1的进行交换
8.重新构建大顶堆
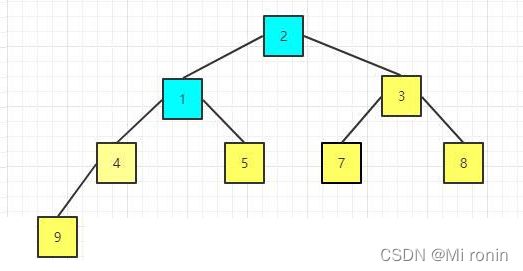
9.重复交换
10.重新构建大顶堆
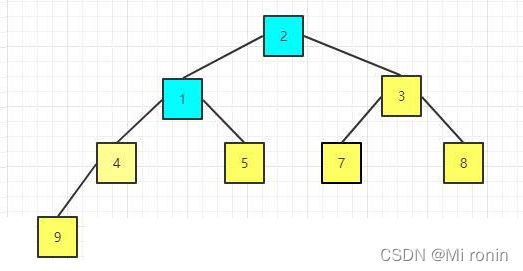
11.重复交换
12.重新构建大顶堆
13.重复交换
14.重新构建大顶堆
15.重复交换
16.重新构建大顶堆
17.重复交换
18.重新构建大顶堆
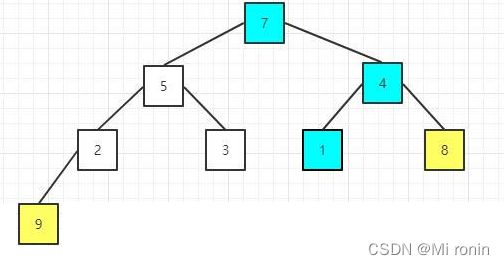
19.继续交换
这里我么就交换结束了 得到了最后的结果。
2.4代码实现
void HeapAdjust(int arr[], int start, int end)
{
//assert
int tmp = arr[start];
for (int i = start * 2 + 1; i <= end; i = start * 2 + 1)//start*2+1 相当于是start这个节点的左孩子
{ //i arr[i])//i tmp)//子大于父
{
arr[start] = arr[i];
start = i;
}
else
{
break;//退出for循环,触发情况2
}
}
arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{
//1.整体从最后一个非叶子节点开始由内到外调整一次
//首先需要知道最后一个非叶子节点的下标
for (int i = (len - 1 - 1) / 2; i >= 0; i--)//因为最后一个非叶子节点肯定是 最后一个叶子节点的父节点
{
HeapAdjust(arr, i, len - 1);//调用我们一次调整函数 //这里第三个值比较特殊,没有规律可言,则直接给最大值len-1
}
//此时,已经调整为大顶堆了
//接下来,根节点的值和当前最后一个节点的值进行交换,然后将尾结点剔除掉
for (int i = 0; i < len - 1; i++)
{
int tmp = arr[0];
arr[0] = arr[len - 1 - i];//len-1-i 是我们当前的尾结点下标
arr[len - 1 - i] = tmp;
HeapAdjust(arr, 0, (len - 1 - i) - 1);//len-1-i 是我们当前的尾结点下标,然后再给其-1则相当于将其剔除出我们的循环
}
}
2.5性能分析
- 时间复杂度:最好和最坏的情况时间复杂度都是(n*logn) 。
- 空间复杂度:O(1)。
- 稳定性:不稳定。
到此这篇关于C语言深入探究冒泡排序与堆排序使用案例讲解的文章就介绍到这了,更多相关C语言排序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!