自协方差函数的Matlab实现
自协方差函数的Matlab实现
文章目录
- 自协方差函数的Matlab实现
-
- 自协方差函数简介
- 上机实验报告
-
- 数据集
- 实验过程
-
- 洗发水销售数据集
- 股票信息数据集
- 参考文献
自协方差函数简介
对于满足均值遍历性和二阶矩遍历性的平稳时间序列一次具体观测值 { x t , t = 1 , 2 , ⋯ , N } \left\{x_{t}, t=1,2, \cdots, N\right\} {xt,t=1,2,⋯,N}, 总体平均可转化为时间平均. 因此, 样本自协方差函数也通常可由下面两种方式计算得到:
{ γ ^ k = 1 N ∑ t = 1 N − k ( x t − μ ^ ) ( x t + k − μ ^ ) , 0 ⩽ k ⩽ N − 1 γ ^ k = γ ^ − k , 1 − N ⩽ k ⩽ − 1 , (1) \begin{cases}\hat{\gamma}_{k}=\frac{1}{N} \sum_{t=1}^{N-k}\left(x_{t}-\hat{\mu}\right)\left(x_{t+k}-\hat{\mu}\right), & 0 \leqslant k \leqslant N-1 \\ \hat{\gamma}_{k}=\hat{\gamma}_{-k}, & 1-N \leqslant k \leqslant-1,\end{cases}\tag{1} {γ^k=N1∑t=1N−k(xt−μ^)(xt+k−μ^),γ^k=γ^−k,0⩽k⩽N−11−N⩽k⩽−1,(1)
或
{ γ ^ k = 1 N − k ∑ t = 1 N − k ( x t − μ ^ ) ( x t + k − μ ^ ) , 0 ⩽ k ⩽ N − 1 γ ^ k = γ ^ − k , 1 − N ⩽ k ⩽ − 1 (2) \begin{cases}\hat{\gamma}_{k}=\frac{1}{N-k} \sum_{t=1}^{N-k}\left(x_{t}-\hat{\mu}\right)\left(x_{t+k}-\hat{\mu}\right), & 0 \leqslant k \leqslant N-1 \\ \hat{\gamma}_{k}=\hat{\gamma}_{-k}, & 1-N \leqslant k \leqslant-1\end{cases}\tag{2} {γ^k=N−k1∑t=1N−k(xt−μ^)(xt+k−μ^),γ^k=γ^−k,0⩽k⩽N−11−N⩽k⩽−1(2)
其中, μ ^ \hat{\mu} μ^ 为平稳序列的均值的估计值. 在实际应用中, 样本自协方差函数的计算通常采用第一种形式.
其原因在于, 利用 ( 1 ) (1) (1) 式定义的样本自协方差函数能使得 N N N 阶的样本自协方差矩阵
Γ ^ N = ( γ ^ k − j ) , k , j = 1 , 2 , ⋯ , N \hat{\boldsymbol{\Gamma}}_{N}=\left(\hat{\gamma}_{k-j}\right), k, j=1,2, \cdots, N Γ^N=(γ^k−j),k,j=1,2,⋯,N
正定.
为了计算自协方差矩阵(ACM),一种最直接的方式是利用两层循环嵌套结构计算,但此方式过于“原始”,对于长期序列计算速度相对比较慢.
注意到, 只要
y j = x j − μ ^ , j = 1 , 2 , ⋯ , N y_{j}=x_{j}-\hat{\mu}, \quad j=1,2, \cdots, N yj=xj−μ^,j=1,2,⋯,N
不全为零, 矩阵
A = ( 0 ⋯ 0 y 1 y 2 ⋯ y N − 1 y N 0 ⋯ y 1 y 2 y 3 ⋯ y N 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ y 1 ⋯ y N − 1 y N 0 ⋯ 0 0 ) N × ( 2 N − 1 ) \boldsymbol{A}=\left(\begin{array}{cccccccc} 0 & \cdots & 0 & y_{1} & y_{2} & \cdots & y_{N-1} & y_{N} \\ 0 & \cdots & y_{1} & y_{2} & y_{3} & \cdots & y_{N} & 0 \\ \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots \\ y_{1} & \cdots & y_{N-1} & y_{N} & 0 & \cdots & 0 & 0 \end{array}\right)_{N \times(2 N-1)} A=⎝⎜⎜⎜⎛00⋮y1⋯⋯⋯0y1⋮yN−1y1y2⋮yNy2y3⋮0⋯⋯⋯yN−1yN⋮0yN0⋮0⎠⎟⎟⎟⎞N×(2N−1)
是行满秩的. 样本自协方差矩阵可表示为
Γ ^ N = ( γ ^ 0 γ ^ 1 ⋯ γ ^ N − 1 γ ^ 1 γ ^ 0 ⋯ γ ^ N − 2 ⋮ ⋮ ⋮ γ ^ N − 1 γ ^ N − 2 ⋯ γ ^ 0 ) = 1 2 A A T \hat{\boldsymbol{\Gamma}}_{N}=\left(\begin{array}{cccc} \hat{\gamma}_{0} & \hat{\gamma}_{1} & \cdots & \hat{\gamma}_{N-1} \\ \hat{\gamma}_{1} & \hat{\gamma}_{0} & \cdots & \hat{\gamma}_{N-2} \\ \vdots & \vdots & & \vdots \\ \hat{\gamma}_{N-1} & \hat{\gamma}_{N-2} & \cdots & \hat{\gamma}_{0} \end{array}\right)=\frac{1}{2} \boldsymbol{A} \boldsymbol{A}^{\mathrm{T}} Γ^N=⎝⎜⎜⎜⎛γ^0γ^1⋮γ^N−1γ^1γ^0⋮γ^N−2⋯⋯⋯γ^N−1γ^N−2⋮γ^0⎠⎟⎟⎟⎞=21AAT
于是,得益于计算机对矩阵并行运算的优化.我们可以采用数组化编程思想,利用矩阵运算,轻松且快速的计算出自协方差矩阵.
上机实验报告
数据集
为了感受不同时间序列的统计性质,选用以下两种数据集分别建模.
- 洗发水销售数据集:
shampoo.csv - 上证指数数据集:
SH600031.csv
实验过程
洗发水销售数据集
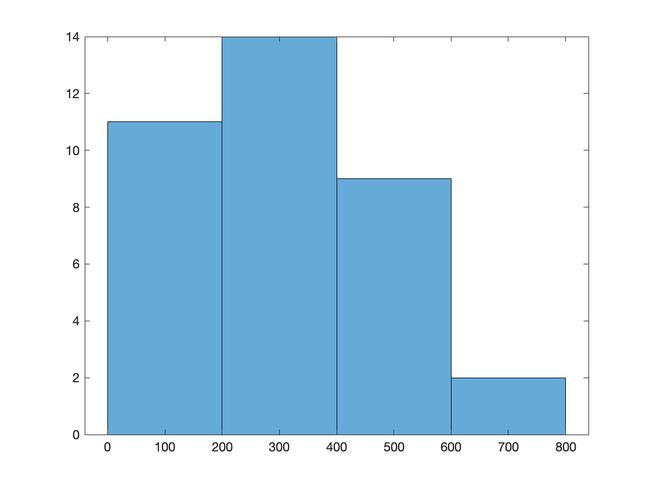
该数据集描述了每月洗发水的销售量
单位是销售计数,有36个观察值.
程序源代码
filename='shampoo.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:36,2);
y=x-mean(x);
A=zeros(length(y),2*length(y)-1);
for i=1:length(y)
A(i,length(y)-i+1:length(y)-i+length(y))=y;
end
ACM=1/length(y).*A*A';
自协方差函数最大值:2.156610448813604e+04
自协方差函数最小值:-6.896521602231956e+03
从图像及数据可以发现:洗发水月销售量具有较明显的子相关性.
股票信息数据集
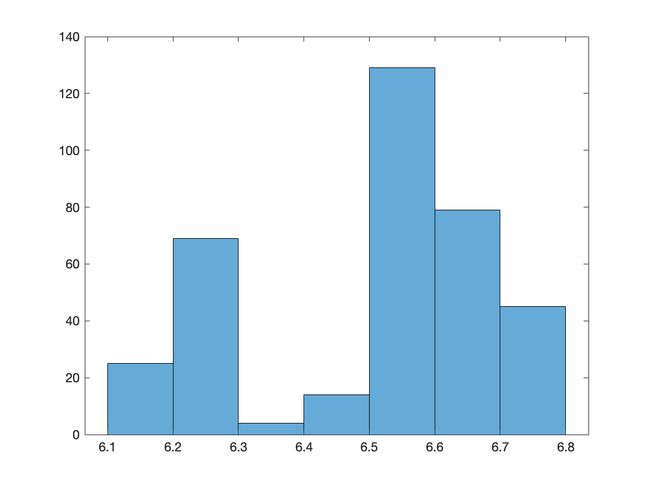
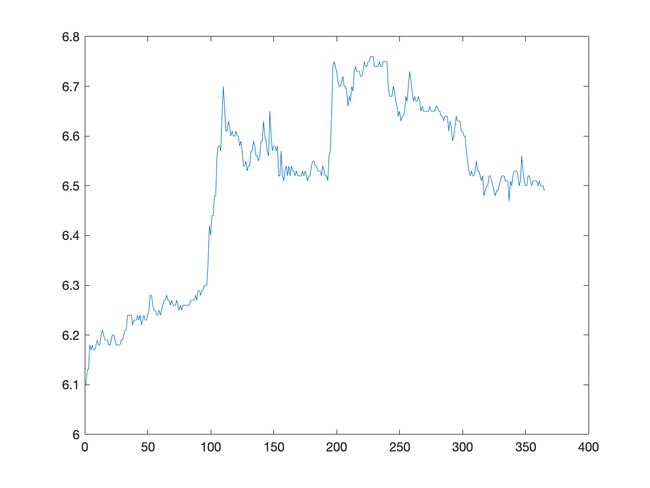
该数据集描述了上证指数每日的开盘,最高,最低,收盘,成交量,成交额.
取连续365天的开盘价进行建模.
程序源代码
filename='SH600031.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:365,3);
y=x-mean(x);
A=zeros(length(y),2*length(y)-1);
for i=1:length(y)
A(i,length(y)-i+1:length(y)-i+length(y))=y;
end
ACM=1/length(y).*A*A';
自协方差函数最大值:0.031476924974325
自协方差函数最小值:-0.013756630793134
从图像及数据可以发现:股市的开盘价没有明显的自相关性.
从时序图及自协方差函数图都能明显看出以上两个时间序列均为非平稳时间序列.
参考文献
周永道,王会琦,吕王勇.时间序列分析及应用.北京:高等教育出版社,2015.
数据集:
SH600031.csv
shampoo.csv
本人非统计专业,若有不妥之处, 恳请批评指正.
作者:图灵的猫
作者邮箱: [email protected]