【雷达信号处理】脉冲多普勒PD及其MATLAB实现

1 原理介绍

1.1 脉冲多普勒过程

我们用脉冲多普勒处理回波信号，目的是测量径向速度，提高信杂比和噪声比。

脉冲多普勒（pulse doppler, PD）处理是多普勒处理的第二大类。在MTI处理中，快时间/慢时间数据矩阵在慢时间维度中经过高通滤波，产生一个新的快时间/慢时间数据序列，其中杂波分量已被衰减。
下图说明了PD处理的原理。
下图显示了计算每个慢时间行数据的离散傅里叶变换（DFT）的每个慢时间行的频谱分析。
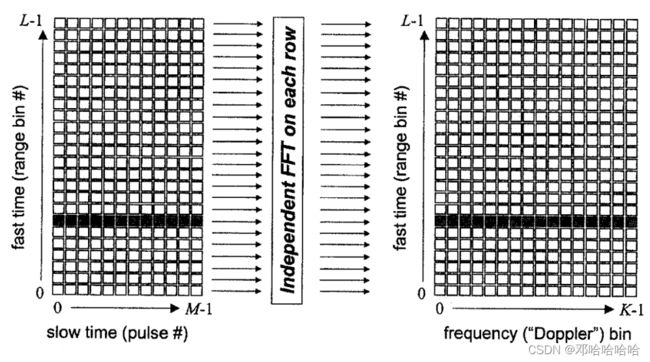因此，PD处理的结果是一个数据矩阵，其维度分别表示快时间和多普勒频率。

1.2 信号模型

1. 发送信号——Chirp信号
   $$S(t_n)=g[t_n,T_p]e^{j\pi \beta {t_n}^2}$$
   其中，$T_p$为脉冲持续时间，$\beta$为调频斜率，$G[t,T_p]$为门宽为$T_p$的门函数。
2. 接受信号
   $$s_b(m,t)=g[(t-{\tau }_m)/T_p]e^{j\pi \beta (t-{\tau }_m{)}^2}{e}^{-j2\pi f_0{\tau }_m}$$
   其中$f_0$为载波频率，${\tau }_m$为第$m$个脉冲的时延$${\tau }_m=2\ast (R_0-m{T}_{r}v)/c$$

1.3 PD的实现

我们可以通过两个步骤实现PD处理。第一步是脉冲压缩，第二步是慢时间FFT。

1. 步骤1：沿距离方向的脉冲压缩
   $$s_1=Asinc(B(t-{\tau }_1))e^{-j2\pi f_o{\tau }_1}$$ $$s_1=Asinc(B(t-{\tau }_1))e^{-j2\pi f_o{\tau }_1}$$ $$....$$ $$s_N=Asinc(B(t-{\tau }_N))e^{-j2\pi f_o{\tau }_N}$$

2. 步骤2：沿着慢时间做FFT
   $$s_{pd}=Asinc(B(t-\tau ))sinc(f-f_d)$$

1.4 相参和非相参累积

1. 相参积累

• 没有信息丢失（振幅或相位）。
• 增益是n，其中n是脉冲数。

2. 非相参积累

• 一些信息丢失（相位）
• 增益约为KaTeX parse error: Expected '}', got 'EOF' at end of input: n^{0.8]
• 在大多数情况下，相干积分比非相干积分更有效。

目标回波的波动会降低积分增益。

2 实验内容

2.1 参数

1. PD 过程

步骤1：

步骤2：

2. 计算速度

根据上图2中最大值出现的位置，算得：

3 MATLAB实现

clear;
close all;
N = 4096;
fs = 100e6;
Ts = 1/fs;
R = 3000;
v = 60;
M = 64;    % PRT（脉冲重复周期）
f0 = 10e9;
Tp = 10e-6;
PRT = 100e-6;
PRF = 1/PRT;
B = 10e6;
c = 3e8;
lambda = c/f0;   % 波长
beta = B/Tp;     % 调频斜率
 
SNR = [0 10 20]; % SNR dB
sigma2 = 1./(10.^(SNR/10));   % 噪声方差
noise_index = 1;
 
echo = zeros(M,N);           % 回波
echo_noise = zeros(M,N);     % 回波+噪声
echo_fft = zeros(M,N);       % fft(回波)
echo_noise_fft = zeros(M,N); % fft 回波+噪声)
 
% 每个脉冲的延迟
tau = zeros(1,M);
for m = 1:M
    tau(1,m) = 2*(R-m*PRT*v)/c;
end
n = 0:N-1;
t = n*Ts;   % 时间范围
% 发送信号
x = rectpuls(t,Tp).*exp(1i*pi*beta*t.^2);
% 接收信号
y = zeros(M,N);
y_noise = zeros(M,N);
for m = 1:M
    tm = tau(m);
    y(m,:) = rectpuls((t-tm),Tp).*exp(1i*pi*beta*(t-tm).^2)*exp(-1i*2*pi*f0*tm);
    y_noise(m,:) = y(m,:) + sqrt(sigma2(noise_index)/2)*(randn(1,N)+1j*randn(1,N));
    % 脉冲压缩
    X = fftshift(fft(x,N));
    Y = fftshift(fft(y(m,:),N));
    Y_noise = fftshift(fft(y_noise(m,:),N));
    S = conj(X).*Y;
    S_noise = conj(X).*Y_noise;
    s = ifft(S);
    s_noise = ifft(S_noise);
    echo(m,:) = s;
    echo_noise(m,:) = s_noise;
end
% coherent sum
% 慢时间FFT
for n = 1:N
    echo_fft(:,n) = fftshift(fft(echo(:,n),M));
    echo_noise_fft(:,n) = fftshift(fft(echo_noise(:,n),M));
end


%% 画图
r = t*c/2;
f = linspace(-1*PRF/2,PRF/2,M);
v = f*c/f0/2;
xaxis = 1:M;
yaxis = r;
figure(1);
% mesh(t,xaxis,abs(echo));
% xlabel('range(m)'),ylabel('time'),zlabel('amplitude');
imagesc(r,(1:M),abs(echo));
title('Pulse Compression');
xlabel('range(m)');
ylabel('slow time');

figure(2);
imagesc(r,v,abs(echo_fft));
% mesh(r,v,abs(echo_fft));
% xlabel('range(m)'),ylabel('doppler'),zlabel('amplitude');
% title('Range-Dopple Heat Map');
title('Pulse Doppler Processing');
xlabel('range(m)');
ylabel('velocity(m/s)');

%% 计算过程
fft_num_m = M;
f_m = (0:fft_num_m-1)*(PRF/fft_num_m);
[column,row]=find(abs(echo_fft)==max(max(abs(echo_fft)))); %row->矩阵列值 column->矩阵行值，所以转置了一下
C = [];
D = [];
% 距离
for a = row-3:row+3
    amp = abs(echo_fft(column-1,a)); % 取幅度值
    C(a) = amp*t(a)*c/2;             %【sum（幅度（i）*距离（i））】
    D(a) = amp;% 幅度值
end
d0 = sum(C)/sum(D); 
%Velocity
E = [];
F = [];
for a_v = column - 3:column + 3%doppler相上 最大值的左右各3个点共7点
    amp_v = abs(echo_fft(a_v,(row-1)));
    E(a_v) = amp_v*f_m(a_v)*lambda/2;
    F(a_v) = amp_v;
end
v0 = sum(E)/sum(F);
fprintf('无噪声时距离:%fm/s\n',d0);
fprintf('无噪声时速度:%fm/s\n',v0);
% 计算增益
% 1.相参积累
[~,index] = max(max(echo_noise));
P_noise = sum(sum(abs(echo_noise(index-10:index-1)).^2)+abs(echo_noise(index+1:index+10)).^2);
co_g = abs(max(max(echo_noise_fft)))^2/(P_noise);
fprintf('相参积累增益: %f dB\n',10*log10(co_g));
% 2.非相参积累
[~,index] = max(transpose(echo_noise));
P_n = sum(sum(abs(echo_noise(index-10:index-1)).^2)+abs(echo_noise(index+1:index+10)).^2);
nco_g = sum(abs(max(transpose(echo_noise_fft))).^2)/M/(P_n);
fprintf('非相参积累增益:%f dB\n',10*log10(nco_g));

参考文献

《雷达信号处理》