脉冲压缩(Pulse Compression, PD)原理与MATLAB实现
这是目录
- 实验原理
-
- 1.1 前情提要
- 1.2 为什么要做脉冲压缩
- 1.3 脉冲压缩过程
- 实验内容
-
- 2.1 实验参数
- 实验结果和分析
-
- 3.1 脉冲压缩的结果
- 全部代码
实验原理
1.1 前情提要
为了获得长的工作范围,雷达需要有长脉冲以获得高能量。同时,为了提高雷达的距离分辨率,要求雷达信号具有较大的带宽。然而,对于简单的未调制脉冲雷达信号,其距离分辨率为 δ r = c / 2 B = c τ / 2 \delta_r=c/2B=c\tau/2 δr=c/2B=cτ/2其中 B B B和 τ \tau τ分别是雷达脉冲的带宽和脉冲持续时间。我们可以看到,带宽和脉冲宽度是相互倒数的,因此工作范围和距离分辨率之间存在着不可调和的矛盾。
1.2 为什么要做脉冲压缩
传统的未调制脉冲雷达系统很难同时获得窄脉冲宽度和宽带宽,但是,如果对长脉冲在其频率或相位上进行调制(即FM,PM),则长脉冲可以具有与短脉冲相同的带宽(距离分辨率)。因此,引入脉冲压缩技术,她允许雷达获得长脉冲的能量和短脉冲的分辨率。
脉冲压缩可以同时提高工作距离和距离分辨率。
方法:
- 我们可以发射更宽的脉冲来提高平均功率,以获得足够的工作范围。
- 接收机采用脉冲压缩算法获得窄脉冲,从而提高距离分辨率。
线性调频(Linear Frequency Modulation, LFM) 信号是脉冲压缩雷达最常用的调制信号,接收时采用匹配滤波进行脉冲压缩。线性调频信号(也称为啁啾信号,chrip signal)的时域表达式如下所示:

其瞬时频率为

其中 k = B / T p k=B/T_p k=B/Tp是频率调制的斜率。 B B B和 T p T_p Tp分别是脉冲带宽和持续时间。我们给出了线性调频信号的一个例子,其时域波形和频谱如下所示。
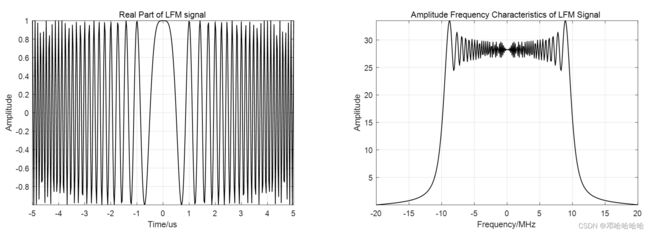
线性调频信号具有较大的带宽延迟积,在脉冲压缩过程中可以获得较高的脉冲压缩比。
1.3 脉冲压缩过程
在接收端,我们使用匹配滤波来实现脉冲压缩。下图展示出了基于LFM信号的脉冲压缩过程。
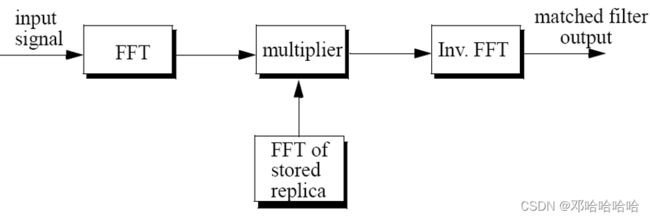 我们在下图中给出了一个脉冲压缩的例子。
我们在下图中给出了一个脉冲压缩的例子。

实验内容
2.1 实验参数
LFM信号模型:
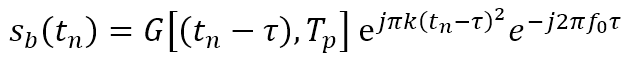
其中, G ( t , T p ) G(t,T_p) G(t,Tp)是门宽为 T p T_p Tp的门函数。其他参数如下所示: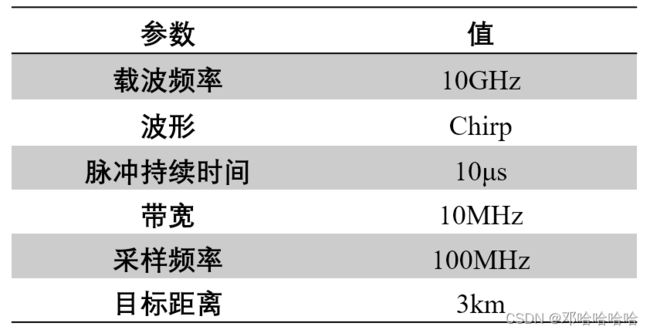 代码:(MATLAB)
代码:(MATLAB)
%% parameters
f0 = 10e9; % 载波
Tp = 10e-6; % 脉冲持续时间
B = 10e6; % 带宽
fs = 100e6; % 采样频率
c = 3e8; % 光速
R0 = 3e3; % 目标距离
k = B/Tp; % 调频斜率
实验结果和分析
3.1 脉冲压缩的结果
(1) 参考信号和回波信号的时域波形
我们回顾一下LFM信号和回波信号的表达式。
参考信号:

回波信号:
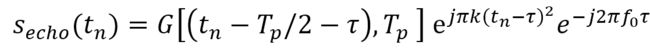
其中, τ = 2 R / c \tau=2R/c τ=2R/c为信号延迟, R R R是目标距离。
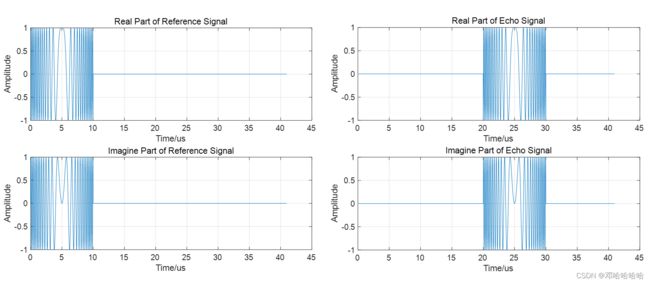 参考信号(左),回波信号(右)
参考信号(左),回波信号(右)
信号生成代码:
%% signal generation
N = 1024*4; % 采样点
n = 0:N-1;
Ts = 1/fs; % 采样间隔
t = n*Ts;
f = -fs/2+ n*(fs/N);
tau_0 = 2*R0/c; % 时延
tau_1 = 2*R1/c;
st = rectpuls(t-Tp/2,Tp).*exp(1i*pi*k*(t-Tp/2).^2); % 参考信号
% 回波信号
secho = rectpuls(t-tau_0-Tp/2,Tp).*exp(1i*pi*k*(t-tau_0-Tp/2).^2)*exp(-1i*2*pi*f0*tau_0);
(2) 脉冲压缩过程
根据前面1.3的叙述,我们首先将回波信号(输入)的频谱乘以参考信号频谱的共轭(乘法器),然后对乘法器的输出做IFFT。因此,我们可以得到匹配滤波器的输出信号。代码如下:
%% 脉冲压缩
Xs = fft(st,N); % 本地副本的FFT
Xecho = fft(secho,N); % 输入信号的FFT
Y = conj(Xs).*Xecho; % 乘法器
Y = fftshift(Y);
y = ifft(Y,N); % IFFT
回波信号的幅频特性和脉冲压缩结果:
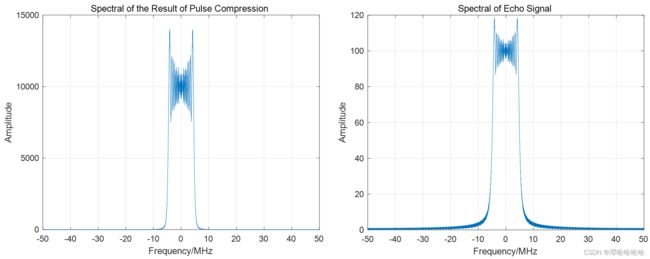
我们可以看到,脉冲压缩结果的频谱振幅是回波信号频谱振幅的平方。
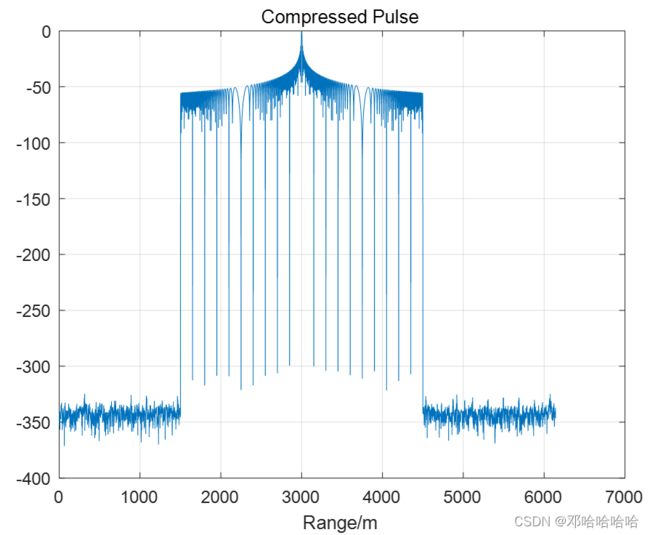
(3) 脉冲压缩结果
我们可以检测到目标的距离为3000m,副瓣比主瓣低约13.4dB。
在多目标环境中,不合适的副瓣可能会掩埋附近较小目标的主瓣,导致目标丢失。为了提高识别多个目标的能力,需要采用旁瓣抑制技术,即加窗技术。
然而,加窗实际上是信号的失配处理。虽然它可以抑制旁瓣,但会降低输出信号的主瓣。换句话说,多目标分辨率的提高是以降低信噪比和距离分辨率为代价的。
全部代码
close all
clc
clear
%% =================== 参数 ======================
f0 = 10e9; % 载波
Tp = 10e-6; % 脉冲持续时间
B = 10e6; % 带宽
fs = 100e6; % 采样频率
c = 3e8; % 光速
R0 = 3e3; % 目标距离
k = B/Tp; % 调频斜率
%% ================= 信号产生 =================
N = 1024*4; % 采样点
n = 0:N-1;
Ts = 1/fs; % 采样间隔
t = n*Ts;
f = -fs/2+ n*(fs/N);
tau_0 = 2*R0/c; % 时延
tau_1 = 2*R1/c;
st = rectpuls(t-Tp/2,Tp).*exp(1i*pi*k*(t-Tp/2).^2); % 参考信号
% 回波信号
secho = rectpuls(t-tau_0-Tp/2,Tp).*exp(1i*pi*k*(t-tau_0-Tp/2).^2)*exp(-1i*2*pi*f0*tau_0);
% two targets
% R1 = 3e3 + 10;
% tau_1 = 2*R1/c;
% echo = rectpuls(t-tau_0-Tp/2,Tp).*exp(1i*2*pi*k*(t-tau_0-Tp/2).^2)*exp(-1i*2*pi*f0*tau_0)+...
rectpuls(t-tau_1-Tp/2,Tp).*exp(1i*2*pi*k*(t-tau_1-Tp/2).^2)*exp(-1i*2*pi*f0*tau_1);
%% =============== 脉冲压缩 ================
Xs = fft(st,N); % 本地副本的FFT
Xecho = fft(secho,N); % 输入信号的FFT
Y = conj(Xs).*Xecho; % 乘法器
Y = fftshift(Y);
y = ifft(Y,N); % IFFT
%% ================== 画图 ======================
figure;
subplot(211);plot(t*1e6,real(st));
xlabel('Time/us');ylabel('Amplitude');
title('Real Part of Reference Signal');grid on;
subplot(212);plot(t*1e6,imag(st));
xlabel('Time/us');ylabel('Amplitude');
title('Imagine Part of Reference Signal');grid on;
echo signal
figure;
subplot(211);plot(t*1e6,real(escho));
xlabel('Time/us');ylabel('Amplitude');
title('Real Part of Echo Signal');grid on;
subplot(212);plot(t*1e6,imag(secho));
xlabel('Time/us');ylabel('Amplitude');
title('Imagine Part of Echo Signal');grid on;
% ============ 频谱 =============
figure;
x1 = fftshift(Xs);
plot(f/1e6,abs(x1));
xlabel('Frequency/Hz');ylabel('Amplitude');
title('Spectral of Reference Signal');grid on;
figure;
plot(f/1e6,abs(fftshift(Xecho)));
xlabel('Frequency/Hz');ylabel('Amplitude');
title('Spectral of Echo Signal');grid on;
figure;
plot(f/1e6,abs(Y));
xlabel('Frequency/Hz');ylabel('Amplitude');
title('Spectral of the Result of Pulse Compression');grid on;
% ========= 脉冲压缩结果 ===========
figure;
r = t*c/2;
y = abs(y)/max(abs(y));
plot(r,20*log10(y));
xlabel('Range/m');title('Result of Pulse Compression');grid on;