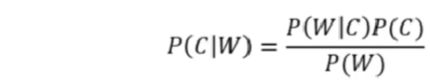机器学习系列(16)_朴素贝叶斯算法

注：机器学习之分类<朴素贝叶斯>

期末会有一道贝叶斯的计算的题目

一、朴素贝叶斯

朴素贝叶斯是一种直接衡量标签和特征之间的概率关系的有监督算法。

1、概率论贝叶斯

2、朴素贝叶斯GaussianNB实例

import numpy as np
from sklearn.naive_bayes import GaussianNB
X = np.array([[-1, -1], [-2, -2], [-3, -3], [-4, -4], [1, 1], [2, 2], [3, 3]])
y = np.array([1, 1, 1, 1, 2, 2, 2])

进行实例化和拟合，构建模型：

clf = GaussianNB()
re = clf.fit(X, y)
print(re)

参数：

re1 = clf.priors
print(re1)  #None

# 设置priors参数值
re2 = clf.set_params(priors=[0.625, 0.375])
print(re2)

# 返回各类标记对应先验概率组成的列表
re3 = clf.priors
print(re3)

re4 = clf.class_prior_
print(re4)

re5 = type(clf.class_prior_) # 类型
print(re5)

re6 = clf.class_count_
print(re6)

re7 = clf.theta_
print(re7)

re8 = clf.sigma_
print(re8)

re9 = clf.get_params(deep=True)
print(re9)

re10 = clf.get_params()
print(re10)

re11 = clf.set_params(priors=[0.625, 0.375])
print(re11)

re12 = clf.fit(X, y, np.array([0.05, 0.05, 0.1, 0.1, 0.1, 0.2, 0.2]))
re13 = clf.theta_
re14 = clf.sigma_
print(re12)
print(re13)
print(re14)

---

对约会数据进行整理：

from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
 
# 读取数据
X = []
Y = []
fr = open("datingTestSet.txt", encoding='utf-8')
print(fr)
index = 0
for line in fr.readlines():
    # print(line)
    line = line.strip() # 去除首位空格
    line = line.split('\t') # 按制表符进行分割
    X.append(line[:3])
    Y.append(line[-1])
 
# 归一化
scaler = MinMaxScaler()
# print(X)
X = scaler.fit_transform(X)
# print(X)
 
# 交叉分类
train_X, test_X, train_y, test_y = train_test_split(X, Y, test_size=0.2)
 
#高斯贝叶斯模型
model = GaussianNB()
model.fit(train_X, train_y)
 
# 预测测试集数据
predicted = model.predict(test_X)
# 输出分类信息
res = metrics.classification_report(test_y, predicted)
# print(res)
# 去重复，得到标签类别
label = list(set(Y))
print(label)
# 输出混淆矩阵信息
matrix_info = metrics.confusion_matrix(test_y, predicted, labels=label)
print(matrix_info)

3、约会实例

from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
 
# 读取数据
X = []
Y = []
fr = open("datingTestSet.txt", encoding='utf-8')
print(fr)
index = 0
for line in fr.readlines():
    # print(line)
    line = line.strip()
    line = line.split('\t')
    X.append(line[:3])
    Y.append(line[-1])
 
# 归一化
scaler = MinMaxScaler()
# print(X)
X = scaler.fit_transform(X)
# print(X)
 
# 交叉分类
train_X, test_X, train_y, test_y = train_test_split(X, Y, test_size=0.2)
 
#高斯贝叶斯模型
model = GaussianNB()
model.fit(train_X, train_y)
 
# 预测测试集数据
predicted = model.predict(test_X)
# 输出分类信息
res = metrics.classification_report(test_y, predicted)
# print(res)
# 去重复，得到标签类别
label = list(set(Y))
print(label)
# 输出混淆矩阵信息
matrix_info = metrics.confusion_matrix(test_y, predicted, labels=label)
print(matrix_info)

import pandas as pd
import numpy as np
import cv2
import time
 
from sklearn.model_selection import train_test_split
from sklearn.metrics  import accuracy_score
 
# 获取数据
def load_data():
    # 读取csv数据
    raw_data = pd.read_csv('bayes_train.csv', header=0)
    data = raw_data.values
    features = data[::, 1::]
    labels = data[::, 0]
    # 避免过拟合，采用交叉验证，随机选取33%数据作为测试集，剩余为训练集
    train_X, test_X, train_y, test_y = train_test_split(features, labels, test_size=0.33, random_state=0)
    return train_X, test_X, train_y, test_y
 
# 二值化处理
def binaryzation(img):
    # 类型转化成Numpy中的uint8型
    cv_img = img.astype(np.uint8)
    # 大于50的值赋值为0，不然赋值为1
    cv2.threshold(cv_img, 50, 1, cv2.THRESH_BINARY_INV, cv_img)
    return cv_img
 
# 训练，计算出先验概率和条件概率
def Train(trainset, train_labels):
    # 先验概率
    prior_probability = np.zeros(class_num)
    # 条件概率
    conditional_probability = np.zeros((class_num, feature_len, 2))
 
    # 计算
    for i in range(len(train_labels)):
        # 图片二值化，让每一个特征都只有0， 1 两种取值
        img = binaryzation(trainset[i])
        label = train_labels[i]
 
        prior_probability[label] += 1
        for j in range(feature_len):
            conditional_probability[label][j][img[j]] += 1
 
    # 将条件概率归到 [1, 10001]
    for i in range(class_num):
        for j in range(feature_len):
            # 经过二值化后图像只有0， 1 两种取值
            pix_0 = conditional_probability[i][i][0]
            pix_1 = conditional_probability[i][j][1]
            # 计算0， 1像素点对应的条件概率
            probability_0 = (float(pix_0)/float(pix_0 + pix_1))*10000 + 1
            probability_1 = (float(pix_1)/float(pix_0 + pix_1))*10000 + 1
 
            conditional_probability[i][j][0] = probability_0
            conditional_probability[i][j][1] = probability_1
 
    return prior_probability, conditional_probability
 
# 计算概率
def calculate_probability(img, label):
    probability = int(prior_probability[label])
    for j in range(feature_len):
        probability *= int(conditional_probability[label][j][img[j]])
    return probability
 
# 预测
def Predict(testset, prior_probability, conditional_probability):
    predict = []
    # 对于每个输入的X，将后验概率最大的类作为X的类输出
    for img in testset:
        # 图像二值化
        img = binaryzation(img)
 
        max_label = 0
        max_probability = calculate_probability(img, 0)
        for j in range(1, class_num):
            probability = calculate_probability(img, j)
            if max_probability < probability:
                max_label = j
                max_probability = probability
        predict.append(max_label)
    return np.array(predict)
 
 
# MNIST数据集有10种labels，分别为“0，1,2，3,4,5,6,7,8,9
class_num = 10
feature_len = 784
 
if __name__ == '__main__':
    time_1 = time.time()
    train_X, test_X, train_y, test_y = load_data()
    prior_probability, conditional_probability = Train(train_X, train_y)
    test_predict = Predict(test_X, prior_probability, conditional_probability)
    score = accuracy_score(test_y, test_predict)
    print(score)

二、朴素贝叶斯实现步骤

• Step 1: Separate By Class 据类分割
  • 要计算数据属于某类的可能性，即可基本概率
  • 需要按类别进行训练数据的分割
  • 可使用dict对象

#自定义据类分割的函数
def separate_by_class(dataset):
	separated = dict()
	for i in range(len(dataset)):
		vector = dataset[i]
		class_value = vector[-1]
		if (class_value not in separated):
			separated[class_value] = list()
		separated[class_value].append(vector)
	return separated

• Step 2: Summarize Dataset 汇总数据
  • 给定数据集需要两个统计数据：平均值和标准差
  • 对每列计算平均值和标准差

#自定义平均值函数
def mean(numbers):
	return sum(numbers)/float(len(numbers))

#自定义标准差函数
def stdev(numbers):
	avg = mean(numbers)
	variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1)
	return sqrt(variance)

#自定义数据集内计算均值和标准差
def summarize_dataset(dataset):
	summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)]
	del(summaries[-1])
	return summaries

#应用
from math import sqrt
dataset = [[3.393533211,2.331273381,0],
	[3.110073483,1.781539638,0],
	[1.343808831,3.368360954,0],
	[3.582294042,4.67917911,0],
	[2.280362439,2.866990263,0],
	[7.423436942,4.696522875,1],
	[5.745051997,3.533989803,1],
	[9.172168622,2.511101045,1],
	[7.792783481,3.424088941,1],
	[7.939820817,0.791637231,1]]
summary = summarize_dataset(dataset)
print(summary)

• Step 3: Summarize Data By Class 按类汇总数据
  • 按类组织训练集中的统计数据

#自定义按类汇总数据集函数
def summarize_by_class(dataset):
	separated = separate_by_class(dataset)
	summaries = dict()
	for class_value, rows in separated.items():
		summaries[class_value] = summarize_dataset(rows)
	return summaries

from math import sqrt
dataset = [[3.393533211,2.331273381,0],
	[3.110073483,1.781539638,0],
	[1.343808831,3.368360954,0],
	[3.582294042,4.67917911,0],
	[2.280362439,2.866990263,0],
	[7.423436942,4.696522875,1],
	[5.745051997,3.533989803,1],
	[9.172168622,2.511101045,1],
	[7.792783481,3.424088941,1],
	[7.939820817,0.791637231,1]]
summary = summarize_by_class(dataset)
for label in summary:
	print(label)
	for row in summary[label]:
		print(row)

• Step 4: Gaussian Probability Density Function 高斯概率密度函数

#自定义计算概率函数
def calculate_probability(x, mean, stdev):
	exponent = exp(-((x-mean)**2 / (2 * stdev**2 )))
	return (1 / (sqrt(2 * pi) * stdev)) * exponent

#测试高斯PDF
from math import sqrt
from math import pi
from math import exp

# Calculate the Gaussian probability distribution function for x
def calculate_probability(x, mean, stdev):
	exponent = exp(-((x-mean)**2 / (2 * stdev**2 )))
	return (1 / (sqrt(2 * pi) * stdev)) * exponent

# Test Gaussian PDF
print(calculate_probability(1.0, 1.0, 1.0))
print(calculate_probability(2.0, 1.0, 1.0))
print(calculate_probability(0.0, 1.0, 1.0))

• Step 5: Class Probabilities 类概率计算
  • 每个类别的概率是单独计算的。这意味着我们首先计算一条新数据属于第一类的概率，然后计算它属于第二类的概率，以此类推。
  • 一条数据属于一个类的概率计算如下：P(类|数据) = P(X|类) * P(类) *不用除法简化计算

#自定义分类概率函数
def calculate_class_probabilities(summaries, row):
	total_rows = sum([summaries[label][0][2] for label in summaries])
	probabilities = dict()
	for class_value, class_summaries in summaries.items():
		probabilities[class_value] = summaries[class_value][0][2]/float(total_rows)
		for i in range(len(class_summaries)):
			mean, stdev, count = class_summaries[i]
			probabilities[class_value] *= calculate_probability(row[i], mean, stdev)
	return probabilities

三、朴素贝叶斯对IRIS进行分类

#计算样例数据的分类概率
from math import sqrt
from math import pi
from math import exp
dataset = [[3.393533211,2.331273381,0],
	[3.110073483,1.781539638,0],
	[1.343808831,3.368360954,0],
	[3.582294042,4.67917911,0],
	[2.280362439,2.866990263,0],
	[7.423436942,4.696522875,1],
	[5.745051997,3.533989803,1],
	[9.172168622,2.511101045,1],
	[7.792783481,3.424088941,1],
	[7.939820817,0.791637231,1]]
summaries = summarize_by_class(dataset)
probabilities = calculate_class_probabilities(summaries, dataset[0])
print(probabilities)
```# 5、Iris案例
```python
# Naive Bayes On The Iris Dataset
from csv import reader
from random import seed
from random import randrange
from math import sqrt
from math import exp
from math import pi
import math


# 加载数据
def load_csv(filename):
	dataset = list()
	with open(filename, 'r') as file:
		csv_reader = reader(file)
		for row in csv_reader:
			if not row:
				continue
			dataset.append(row)
	return dataset

# 将数据转换为float
def str_column_to_float(dataset, column):
	for row in dataset:
		row[column] = float(row[column].strip())

# 将数据转换为integer
def str_column_to_int(dataset, column):
    class_values = [row[column] for row in dataset]
    unique = set(class_values)
    lookup = dict()
    for i, value in enumerate(unique):
        lookup[value] = i
        print('[%s] => %d' % (value, i))
    for row in dataset:
        row[column] = lookup[row[column]]
    return lookup

# 将数据集拆分为k折
def cross_validation_split(dataset, n_folds):
	dataset_split = list()
	dataset_copy = list(dataset)
	fold_size = int(len(dataset) / n_folds)
	for _ in range(n_folds):
		fold = list()
		while len(fold) < fold_size:
			index = randrange(len(dataset_copy))
			fold.append(dataset_copy.pop(index))
		dataset_split.append(fold)
	return dataset_split

# 计算准确性百分比
def accuracy_metric(actual, predicted):
	correct = 0
	for i in range(len(actual)):
		if actual[i] == predicted[i]:
			correct += 1
	return correct / float(len(actual)) * 100.0

# 使用交叉验证评估算法
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
	folds = cross_validation_split(dataset, n_folds)
	scores = list()
	for fold in folds:
		train_set = list(folds)
		train_set.remove(fold)
		train_set = sum(train_set, [])
		test_set = list()
		for row in fold:
			row_copy = list(row)
			test_set.append(row_copy)
			row_copy[-1] = None
		predicted = algorithm(train_set, test_set, *args)
		actual = [row[-1] for row in fold]
		accuracy = accuracy_metric(actual, predicted)
		scores.append(accuracy)
	return scores

# 据类分割数据，返回字段
def separate_by_class(dataset):
	separated = dict()
	for i in range(len(dataset)):
		vector = dataset[i]
		class_value = vector[-1]
		if (class_value not in separated):
			separated[class_value] = list()
		separated[class_value].append(vector)
	return separated

# 返回平均值
def mean(numbers):
	return sum(numbers)/float(len(numbers))

# 计算标准差
def stdev(numbers):
	avg = mean(numbers)
	variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1)
	return sqrt(variance)

# 计算每列的均值与标准差
def summarize_dataset(dataset):
	summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)]
	del(summaries[-1])
	return summaries

# 据类分割数据集计算每行统计指标
def summarize_by_class(dataset):
	separated = separate_by_class(dataset)
	summaries = dict()
	for class_value, rows in separated.items():
		summaries[class_value] = summarize_dataset(rows)
	return summaries

# 计算高斯PDF
def calculate_probability(x, mean, stdev):
    exponent=exp(-((x-mean)**2 / (2 * stdev**2 )))
    return (1 / (math.sqrt(2 * pi) * math.pow(stdev,2))) * exponent

# 计算每行给定数据的分类预测概率
def calculate_class_probabilities(summaries, row):
	total_rows = sum([summaries[label][0][2] for label in summaries])
	probabilities = dict()
	for class_value, class_summaries in summaries.items():
		probabilities[class_value] = summaries[class_value][0][2]/float(total_rows)
		for i in range(len(class_summaries)):
			mean, stdev, _ = class_summaries[i]
			probabilities[class_value] *= calculate_probability(row[i], mean, stdev)
	return probabilities

# 对给定的数据进行分类预测
def predict(summaries, row):
	probabilities = calculate_class_probabilities(summaries, row)
	best_label, best_prob = None, -1
	for class_value, probability in probabilities.items():
		if best_label is None or probability > best_prob:
			best_prob = probability
			best_label = class_value
	return best_label

# 定义贝叶斯算法
def naive_bayes(train, test):
	summarize = summarize_by_class(train)
	predictions = list()
	for row in test:
		output = predict(summarize, row)
		predictions.append(output)
	return(predictions)


# 在iris数据集上测试贝叶斯算法
seed(1)
filename = 'iris无索引.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
	str_column_to_float(dataset, i)
    
# 将类转换为整型
str_column_to_int(dataset, len(dataset[0])-1)
# 评估算法
n_folds = 5
scores = evaluate_algorithm(dataset, naive_bayes, n_folds)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))
# 总的准确速度

给定一个数据集，测试它的分类：

str_column_to_int(dataset, len(dataset[0])-1)
model = summarize_by_class(dataset)
# 数据集给定要符合相相关要求
row = [5.0,3.3,1.4,0.2]
# 预测分类标签
label = predict(model, row)
3print('Data=%s, Predicted: %s' % (row, label))

---

from sklearn import datasets
iris = datasets.load_iris() #直接调用数据中台的数据

from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()#拟合
clf = clf.fit(iris.data, iris.target)#建立模型
y_pred=clf.predict(iris.data)#做预测
print("高斯朴素贝叶斯，样本总数： %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_pred).sum()))