基于蛇优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、蛇优化算法
-
- (1)初始化
- (2)种群分为两组—雄性和雌性
- (3)评估每组并确定温度和食物量
- (4)探索阶段(无食物)
- (5)开发阶段(食物存在)
- 2、SO算法伪代码
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、蛇优化算法
文献[1]受蛇的特殊交配行为的启发,提出了一种新的自然启发的元启发式算法,称为蛇优化算法(Snake Optimizer, SO)。
(1)初始化
与所有的元启发式算法一样,SO从生成均匀分布的随机种群开始,以便能够开始优化算法过程。可使用下式获得初始种群: X i = X min + r × ( X max − X min ) (1) X_i=X_{\min}+r\times(X_{\max}-X_{\min})\tag{1} Xi=Xmin+r×(Xmax−Xmin)(1)其中, X i X_i Xi是第 i i i个个体的位置, r r r是介于0和1之间的随机数, X min X_{\min} Xmin和 X max X_{\max} Xmax分别是问题的下界和上界。
(2)种群分为两组—雄性和雌性
假设雄性个数占50%,雌性个数占50%。种群分为两组:雄性组和雌性组。使用式(2)和(3)来划分种群。 N m ≈ N / 2 (2) N_m\approx N/2\tag{2} Nm≈N/2(2) N f = N − N m (3) N_f=N-N_m\tag{3} Nf=N−Nm(3)其中, N N N是种群个体总数, N m N_m Nm表示雄性个体数, N f N_f Nf表示雌性个体数。
(3)评估每组并确定温度和食物量
- 找到每组中最好的个体,得到最佳的雄性个体( f b e s t , m f_{best,m} fbest,m)和最佳的雌性个体( f b e s t , f f_{best,f} fbest,f)以及食物位置( f f o o d f_{food} ffood)。
- 使用下式计算温度: Temp = exp ( − t T ) (4) \text{Temp}=\exp\left(-\frac tT\right)\tag{4} Temp=exp(−Tt)(4)其中, t t t表示当前迭代次数, T T T表示最大迭代次数。
- 食物量( Q \text{Q} Q)使用下式计算: Q = c 1 ∗ exp ( t − T T ) (5) \text{Q}=c_1*\exp\left(\frac{t-T}{T}\right)\tag{5} Q=c1∗exp(Tt−T)(5)其中, c 1 c_1 c1是值为0.5的常数。
(4)探索阶段(无食物)
如果 Q < Threshold ( Threshold = 0.25 ) Q<\text{Threshold}(\text{Threshold}=0.25) Q<Threshold(Threshold=0.25),蛇会通过选择任意位置来搜索食物,并更新它们相对于食物的位置。要模拟探索阶段,需执行以下操作: X i , m ( t + 1 ) = X r a n d , m ( t ) ± c 2 × A m × ( ( X max − X min ) × r a n d + X min ) (6) X_{i,m}(t+1)=X_{rand,m}(t)\pm c_2\times A_m\times((X_{\max}-X_{\min})\times rand+X_{\min})\tag{6} Xi,m(t+1)=Xrand,m(t)±c2×Am×((Xmax−Xmin)×rand+Xmin)(6)其中, X i , m X_{i,m} Xi,m表示第 i i i个雄性个体位置, X r a n d , m X_{rand,m} Xrand,m表示随机雄性个体的位置, r a n d rand rand是介于0和1之间的随机数, A m A_m Am是雄性个体寻找食物的能力,计算如下: A m = exp ( − f r a n d , m f i , m ) (7) A_m=\exp\left(-\frac{f_{rand,m}}{f_{i,m}}\right)\tag{7} Am=exp(−fi,mfrand,m)(7)其中, f r a n d , m f_{rand,m} frand,m是 X r a n d , m X_{rand,m} Xrand,m的适应度值, f i , m f_{i,m} fi,m是第 i i i个雄性个体的适应度值, c 2 c_2 c2是值为0.05的常数。 X i , f = X r a n d , f ( t + 1 ) ± c 2 × A f × ( ( X max − X min ) × r a n d + X min ) (8) X_{i,f}=X_{rand,f}(t+1)\pm c_2\times A_f\times((X_{\max}-X_{\min})\times rand+X_{\min})\tag{8} Xi,f=Xrand,f(t+1)±c2×Af×((Xmax−Xmin)×rand+Xmin)(8)其中, X i , f X_{i,f} Xi,f表示第 i i i个雌性个体的位置, X r a n d , f X_{rand,f} Xrand,f表示随机雌性个体的位置, r a n d rand rand是介于0和1之间的随机数, A f A_f Af是雌性个体寻找食物的能力,计算如下: A f = exp ( − f r a n d , f f i , f ) (9) A_f=\exp\left(-\frac{f_{rand,f}}{f_{i,f}}\right)\tag{9} Af=exp(−fi,ffrand,f)(9)其中, f r a n d , f f_{rand,f} frand,f是 X r a n d , f X_{rand,f} Xrand,f的适应度值, f i , f f_{i,f} fi,f是第 i i i个雌性个体的适应度值。
(5)开发阶段(食物存在)
在 Q > Threshold \text{Q}>\text{Threshold} Q>Threshold的前提下,如果满足 Temp > Threshold ( 0.6 ) \text{Temp}>\text{Threshold}(0.6) Temp>Threshold(0.6)(炎热),此时蛇只会向食物方向移动。 X i , j ( t + 1 ) = X f o o d ± c 3 × Temp × r a n d × ( X f o o d − X i , j ( t ) ) (10) X_{i,j}(t+1)=X_{food}\pm c_3\times\text{Temp}\times rand\times(X_{food}-X_{i,j}(t))\tag{10} Xi,j(t+1)=Xfood±c3×Temp×rand×(Xfood−Xi,j(t))(10)其中, X i , j X_{i,j} Xi,j是所有个体(雄性和雌性)的位置, X f o o d X_{food} Xfood是最佳个体的位置, c 3 c_3 c3是值为2的常数。
如果满足 Temp < Threshold ( 0.6 ) \text{Temp}<\text{Threshold}(0.6) Temp<Threshold(0.6)(寒冷),此时蛇将处于战斗模式或交配模式。
- 当蛇处于战斗模式时: X i , m ( t + 1 ) = X i , m ( t ) ± c 3 × F M × r a n d × ( Q × X b e s t , f − X i , m ( t ) ) (11) X_{i,m}(t+1)=X_{i,m}(t)\pm c_3\times FM\times rand\times(\text Q\times X_{best,f}-X_{i,m}(t))\tag{11} Xi,m(t+1)=Xi,m(t)±c3×FM×rand×(Q×Xbest,f−Xi,m(t))(11)其中, X i , m X_{i,m} Xi,m表示第 i i i个雄性个体的位置, X b e s t , f X_{best,f} Xbest,f表示雌性群体中最佳个体的位置, F M FM FM表示雄性个体的战斗能力。 X i , f ( t + 1 ) = X i , f ( t ) ± c 3 × F F × r a n d × ( Q × X b e s t , m − X i , f ( t ) ) (12) X_{i,f}(t+1)=X_{i,f}(t)\pm c_3\times FF\times rand\times(\text Q\times X_{best,m}-X_{i,f}(t))\tag{12} Xi,f(t+1)=Xi,f(t)±c3×FF×rand×(Q×Xbest,m−Xi,f(t))(12)其中, X i , f X_{i,f} Xi,f表示第 i i i个雌性个体的位置, X b e s t , m X_{best,m} Xbest,m表示雄性群体中最佳个体的位置, F F FF FF表示雌性个体的战斗能力。
F M FM FM和 F F FF FF可通过下式计算: F M = exp ( − f b e s t , f f i ) (13) FM=\exp\left(-\frac{f_{best,f}}{f_i}\right)\tag{13} FM=exp(−fifbest,f)(13) F F = exp ( − f b e s t , m f i ) (14) FF=\exp\left(-\frac{f_{best,m}}{f_i}\right)\tag{14} FF=exp(−fifbest,m)(14)其中, f b e s t , f f_{best,f} fbest,f是雌性群体中最佳个体的适应度, f b e s t , m f_{best,m} fbest,m是雄性群体中最佳个体的适应度, f i f_i fi是当前个体的适应度。 - 当蛇处于交配模式时: X i , m ( t + 1 ) = X i , m ( t ) ± c 3 × M m × r a n d × ( Q × X i , f ( t ) − X i , m ( t ) ) (15) X_{i,m}(t+1)=X_{i,m}(t)\pm c_3\times M_m\times rand\times(\text Q\times X_{i,f}(t)-X_{i,m}(t))\tag{15} Xi,m(t+1)=Xi,m(t)±c3×Mm×rand×(Q×Xi,f(t)−Xi,m(t))(15) X i , f ( t + 1 ) = X i , f ( t ) ± c 3 × M f × r a n d × ( Q × X i , m ( t ) − X i , f ( t ) ) (16) X_{i,f}(t+1)=X_{i,f}(t)\pm c_3\times M_f\times rand\times(\text Q\times X_{i,m}(t)-X_{i,f}(t))\tag{16} Xi,f(t+1)=Xi,f(t)±c3×Mf×rand×(Q×Xi,m(t)−Xi,f(t))(16)其中, X i , f X_{i,f} Xi,f是第 i i i个雌性个体的位置, X i , m X_{i,m} Xi,m是第 i i i个雄性个体的位置, M m M_m Mm和 M f M_f Mf分别是雄性和雌性的交配能力,可计算如下: M m = exp ( − f i , f f i , m ) (17) M_m=\exp\left(-\frac{f_{i,f}}{f_{i,m}}\right)\tag{17} Mm=exp(−fi,mfi,f)(17) M f = exp ( − f i , m f i , f ) (18) M_f=\exp\left(-\frac{f_{i,m}}{f_{i,f}}\right)\tag{18} Mf=exp(−fi,ffi,m)(18)如果蛋孵化,选择最差的雄性和雌性个体并替换它们: X w o r s t , m = X min + r a n d × ( X max − X min ) (19) X_{worst,m}=X_{\min}+rand\times(X_{\max}-X_{\min})\tag{19} Xworst,m=Xmin+rand×(Xmax−Xmin)(19) X w o r s t , f = X min + r a n d × ( X max − X min ) (20) X_{worst,f}=X_{\min}+rand\times(X_{\max}-X_{\min})\tag{20} Xworst,f=Xmin+rand×(Xmax−Xmin)(20)其中, X w o r s t , m X_{worst,m} Xworst,m是最差的雄个体, X w o r s t , f X_{worst,f} Xworst,f是最差的雌性个体。
2、SO算法伪代码
二、仿真实验与结果分析
将SO与MFO、HHO和WOA进行对比,以CEC2017测试函数中的F1、F2(单峰函数/30维),F5、F6(简单多峰函数/30维)、F14、F15(混合函数/30维)、F23、F24(合成函数/30位),实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:
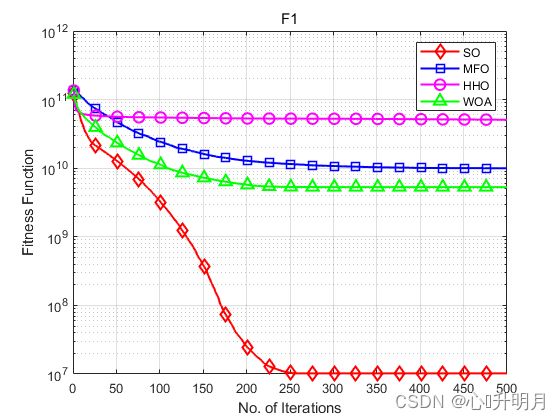



函数:F1
SO:最差值:33974673.7307,最优值:1155333.672,平均值:10196011.2452,标准差:10254370.6097,秩和检验:1
MFO:最差值:29115737344.125,最优值:1365731153.716,平均值:9963494991.0887,标准差:7914826555.6681,秩和检验:3.0199e-11
HHO:最差值:65049090447.8205,最优值:35245462786.294,平均值:50849509866.1387,标准差:7324690706.6761,秩和检验:3.0199e-11
WOA:最差值:9471165065.8515,最优值:1987532979.0067,平均值:5297462938.994,标准差:1868211383.1812,秩和检验:3.0199e-11
函数:F2
SO:最差值:89771.8089,最优值:52558.7692,平均值:69986.3462,标准差:9649.2405,秩和检验:1
MFO:最差值:312557.7779,最优值:86620.335,平均值:185422.9748,标准差:65351.7631,秩和检验:3.6897e-11
HHO:最差值:93162.1726,最优值:76055.8727,平均值:89794.4644,标准差:3707.603,秩和检验:2.3715e-10
WOA:最差值:414014.7119,最优值:131543.3979,平均值:262109.8029,标准差:77417.8965,秩和检验:3.0199e-11
函数:F5
SO:最差值:630.4691,最优值:607.6786,平均值:617.0331,标准差:6.688,秩和检验:1
MFO:最差值:677.3797,最优值:620.2406,平均值:641.7679,标准差:14.3667,秩和检验:6.722e-10
HHO:最差值:701.0952,最优值:669.9093,平均值:684.2152,标准差:7.6866,秩和检验:3.0199e-11
WOA:最差值:717.6984,最优值:658.1284,平均值:680.385,标准差:12.3442,秩和检验:3.0199e-11
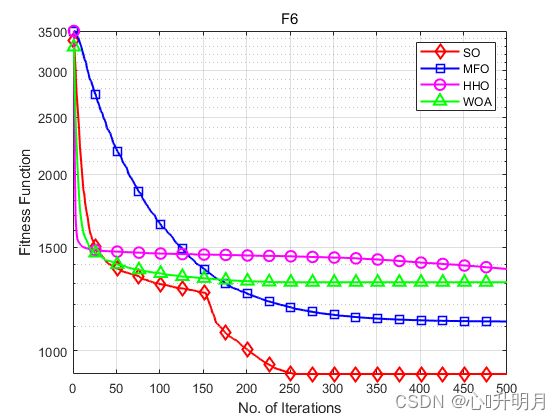
函数:F6
SO:最差值:987.1854,最优值:835.0802,平均值:912.8178,标准差:41.1131,秩和检验:1
MFO:最差值:1839.3778,最优值:853.1182,平均值:1121.697,标准差:264.1183,秩和检验:1.2493e-05
HHO:最差值:1451.4651,最优值:1227.5803,平均值:1378.0648,标准差:47.3223,秩和检验:3.0199e-11
WOA:最差值:1521.9355,最优值:1133.224,平均值:1308.4355,标准差:88.6087,秩和检验:3.0199e-11
函数:F14
SO:最差值:56298.7091,最优值:2785.1689,平均值:16945.7969,标准差:15113.6619,秩和检验:1
MFO:最差值:120041.348,最优值:4741.575,平均值:42709.3347,标准差:28102.5705,秩和检验:1.4298e-05
HHO:最差值:2342601244.6978,最优值:488004.3141,平均值:359936905.7366,标准差:507183244.3008,秩和检验:3.0199e-11
WOA:最差值:34848733.8535,最优值:462489.2436,平均值:5624854.7648,标准差:8061511.2733,秩和检验:3.0199e-11
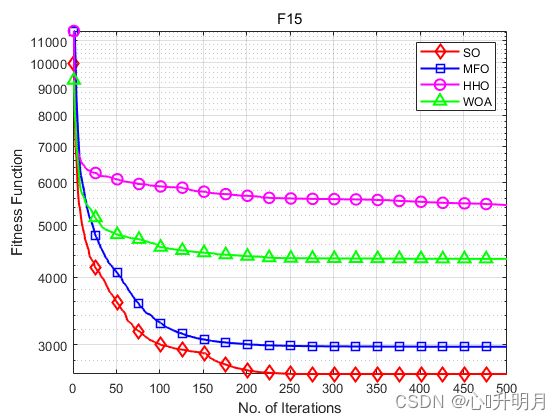
函数:F15
SO:最差值:3163.7247,最优值:2109.8214,平均值:2646.0954,标准差:279.0975,秩和检验:1
MFO:最差值:3778.2905,最优值:2340.7927,平均值:2972.5303,标准差:361.0532,秩和检验:0.00090307
HHO:最差值:9846.4461,最优值:3770.6534,平均值:5443.3361,标准差:1587.9875,秩和检验:3.0199e-11
WOA:最差值:6082.3881,最优值:3388.2027,平均值:4328.3335,标准差:577.7778,秩和检验:3.0199e-11
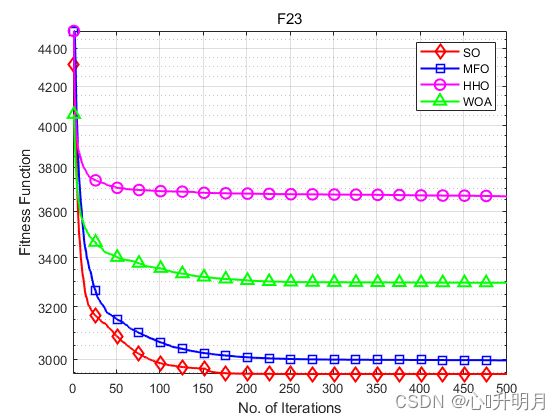
函数:F23
SO:最差值:3043.5774,最优值:2895.7575,平均值:2945.502,标准差:33.0863,秩和检验:1
MFO:最差值:3059.3567,最优值:2922.609,平均值:2995.1531,标准差:36.9215,秩和检验:3.5708e-06
HHO:最差值:4078.6594,最优值:3400.9435,平均值:3666.0339,标准差:170.655,秩和检验:3.0199e-11
WOA:最差值:3512.2775,最优值:3113.2449,平均值:3295.8396,标准差:105.6938,秩和检验:3.0199e-11
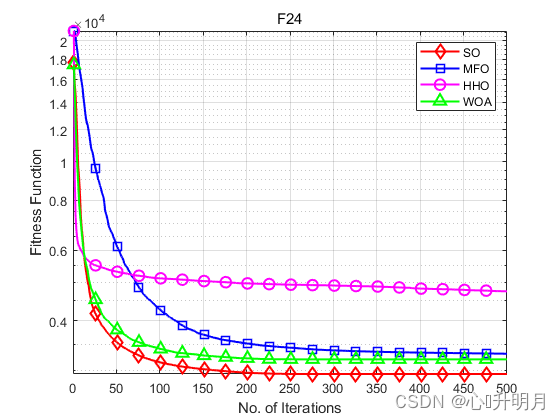
函数:F24
SO:最差值:3027.5599,最优值:2895.514,平均值:2945.9496,标准差:34.5178,秩和检验:1
MFO:最差值:4716.7118,最优值:2909.5645,平均值:3309.8719,标准差:425.8871,秩和检验:7.043e-07
HHO:最差值:5747.3332,最优值:4048.9975,平均值:4739.2239,标准差:400.0802,秩和检验:3.0199e-11
WOA:最差值:3412.9083,最优值:3071.8852,平均值:3204.753,标准差:84.7944,秩和检验:3.0199e-11
实验结果表明了SO算法在不同场景的探索—开发平衡和收敛曲线速度方面的有效性。
三、参考文献
[1] Fatma A. Hashim, Abdelazim G. Hussien. Snake Optimizer: A novel meta-heuristic optimization algorithm[J]. Knowledge-Based Systems, 2022, 242: 108320.
