CS224N WINTER 2022(三)RNN、语言模型、梯度消失与梯度爆炸(附Assignment3答案)
CS224N WINTER 2022(一)词向量(附Assignment1答案)
CS224N WINTER 2022(二)反向传播、神经网络、依存分析(附Assignment2答案)
CS224N WINTER 2022(三)RNN、语言模型、梯度消失与梯度爆炸(附Assignment3答案)
CS224N WINTER 2022(四)机器翻译、注意力机制、subword模型(附Assignment4答案)
CS224N WINTER 2022(五)Transformers详解(附Assignment5答案)
序言
-
CS224N WINTER 2022课件可从https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1224/下载,也可从下面网盘中获取:
https://pan.baidu.com/s/1LDD1H3X3RS5wYuhpIeJOkA 提取码: hpu3本系列博客每个小节的开头也会提供该小结对应课件的下载链接。
-
课件、作业答案、学习笔记(Updating):GitHub@cs224n-winter-2022
-
关于本系列博客内容的说明:
-
笔者根据自己的情况记录较为有用的知识点,并加以少量见解或拓展延申,并非slide内容的完整笔注;
-
CS224N WINTER 2022共计五次作业,笔者提供自己完成的参考答案,不担保其正确性;
-
由于CSDN限制博客字数,笔者无法将完整内容发表于一篇博客内,只能分篇发布,可从我的GitHub Repository中获取完整笔记,本系列其他分篇博客发布于(Updating):
CS224N WINTER 2022(一)词向量(附Assignment1答案)
CS224N WINTER 2022(二)反向传播、神经网络、依存分析(附Assignment2答案)
CS224N WINTER 2022(三)RNN、语言模型、梯度消失与梯度爆炸(附Assignment3答案)
CS224N WINTER 2022(四)机器翻译、注意力机制、subword模型(附Assignment4答案)
CS224N WINTER 2022(五)Transformers详解(附Assignment5答案)
-
文章目录
- 序言
-
- lecture 5 循环神经网络和语言模型
-
- slides
- notes
- suggested readings
- assignment3 参考答案
-
- 1. Machine Learning & Neural Networks
- 2. Neural Transition-Based Dependency Parsing
- lecture 6 梯度消失与爆炸,变体RNN,seq2seq
-
- slides
- notes
- suggested readings
lecture 5 循环神经网络和语言模型
slides
[slides]
-
神经依存分析模型架构:slides p.4
常规的依存分析方法涉及的类别特征是稀疏且不完整的,因此需要耗费大量时间用于特征运算;神经网络方法可以学习得到稠密的特征表示来更好地解决问题。
这里再次提到lecture3的notes部分提到的greedy Greedy Deterministic Transition-Based Parsing的例子,神经网络在给定状态三元组 ( σ , β , A ) (\sigma,\beta,A) (σ,β,A)的特征表示下,对下一次可能的转移(三种转移策略之一)进行预测。
与Neural transition-based依存解析模型对应,也有Neural graph-based依存解析模型,它要预测的就是图节点(单词)之间的依存关系是否存在,有点类似证明图。
### notes
-
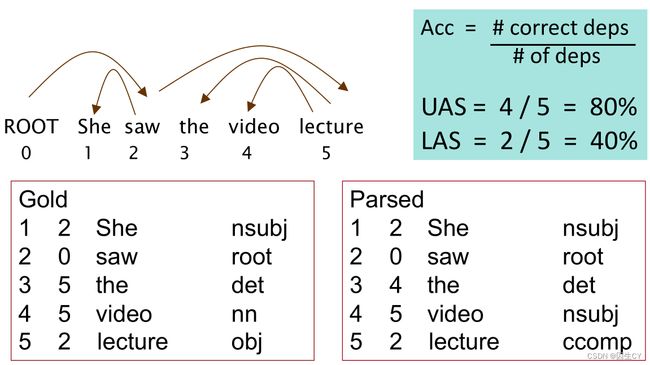
神经依存分析的评估指标:slides p.5
左边的Gold是依存分析训练集的标注格式,包括词性标注的预测以及依赖关系的预测。
看起来UAS是依赖关系的精确度,LAS是词性标注的精确度。(这么解释是合理的)
正好在看这部分又查阅到另一篇博客,感觉讲得比我清楚。
-
神经网络参数初始化:slides p.16
这个在lecture3的式 ( 3.7 ) (3.7) (3.7)中也有提过一次,这里提到的初始化规则是:
-
截距项初始化为零;
-
权重矩阵的数值在 Uniform ( − r , r ) \text{Uniform}(-r,r) Uniform(−r,r)的分布上采样,尽量确保初始值的方差满足下式:
Var ( W i ) = 2 n i n + n o u t (5.1) \text{Var}(W_i)=\frac2{n_{\rm in}+n_{\rm out}}\tag{5.1} Var(Wi)=nin+nout2(5.1)
其中 n i n n_{\rm in} nin与 n o u t n_{\rm out} nout分别表示 W i W_i Wi的fan-in与fan-out;
-
-
语言模型:slides p.19-22
语言模型旨在给定单词序列的条件下,预测下一个单词是什么(输入法的联想):
P ( x ( t + 1 ) ∣ x ( t ) , . . . , x ( 1 ) ) (5.2) P(x^{(t+1)}|x^{(t)},...,x^{(1)})\tag{5.2} P(x(t+1)∣x(t),...,x(1))(5.2)
也可以看作是计算一段文本出现的概率(文本校正):
P ( x ( 1 ) , . . . , x ( T ) ) = P ( x ( 1 ) ) × P ( x ( 2 ) ∣ x ( 1 ) ) × . . . × P ( x ( T ) ∣ x ( T − 1 ) , . . . , x ( 1 ) ) = ∏ t = 1 T P ( x ( t ) ∣ x ( t − 1 ) , . . . , x ( 1 ) ) (5.3) \begin{aligned} P(x^{(1)},...,x^{(T)})&=P(x^{(1)})\times P(x^{(2)}|x^{(1)})\times...\times P(x^{(T)}|x^{(T-1)},...,x^{(1)})\\ &=\prod_{t=1}^TP(x^{(t)}|x^{(t-1)},...,x^{(1)}) \end{aligned}\tag{5.3} P(x(1),...,x(T))=P(x(1))×P(x(2)∣x(1))×...×P(x(T)∣x(T−1),...,x(1))=t=1∏TP(x(t)∣x(t−1),...,x(1))(5.3) -
n-gram模型:slides p.23-32
最经典的统计语言模型莫过于n-gram模型,即只考虑长度不超过n的单词序列的转移概率与分布概率,假定:
P ( x ( t + 1 ) ∣ x ( t ) , . . . , x ( 1 ) ) = P ( x ( t + 1 ) ∣ x ( t ) , . . . , x ( t − n + 2 ) ) = P ( x ( t + 1 ) , x ( t ) , . . . , x ( t − n + 2 ) ) P ( x ( t ) , . . . , x ( t − n + 2 ) ) ≈ count ( x ( t + 1 ) , x ( t ) , . . . , x ( t − n + 2 ) ) count ( x ( t ) , . . . , x ( t − n + 2 ) ) (5.4) \begin{aligned} P(x^{(t+1)}|x^{(t)},...,x^{(1)})&=P(x^{(t+1)}|x^{(t)},...,x^{(t-n+2)})\\ &=\frac{P(x^{(t+1)},x^{(t)},...,x^{(t-n+2)})}{P(x^{(t)},...,x^{(t-n+2)})}\\ &\approx\frac{\text{count}(x^{(t+1)},x^{(t)},...,x^{(t-n+2)})}{\text{count}(x^{(t)},...,x^{(t-n+2)})} \end{aligned}\tag{5.4} P(x(t+1)∣x(t),...,x(1))=P(x(t+1)∣x(t),...,x(t−n+2))=P(x(t),...,x(t−n+2))P(x(t+1),x(t),...,x(t−n+2))≈count(x(t),...,x(t−n+2))count(x(t+1),x(t),...,x(t−n+2))(5.4)最终可以使用大规模语料库中的统计结果进行近似。
当然这种假定可能并不总是正确,因为文本中的相互关联的单词可能会间隔很远,并不仅能通过前方少数几个单词就能正确推断下一个单词。
总体来说,n-gram模型的存在如下两个显著的缺陷:
-
稀疏性:可能一段文本根本就从来没有出现过;
-
高内存占用:存储文本中所有的n-gram值耗用非常大,因此一般n的取值都很小。这里笔者可以推荐一个公开的英文2-gram与3-gram数据,以arpa格式的文件存储,具体使用可以参考笔者的博客。
-
-
神经语言模型与RNN:slides p.33
这种解决与序列预测相关的学习任务,正是RNN大展身手的时候,损失函数使用交叉熵。
由于大多是RNN的基础内容,没有特别值得记录的内容,提醒一下RNN是串行结构,因此无法并行提速。
这里记录slides中几个小demo的项目地址:
-
使用n-gram模型自动生成文本:language-models
-
利用RNN语言模型生成奥巴马讲话:obama-rnn-machine-generated-political-speeches
-
自动智能写作(模仿哈利波特小说风格):how-to-write-with-artificial-intelligence
-
-
语言模型评估指标:slides p.56
- 标准的语言模型评估指标是混乱度(perplexity):
perplexity = ∏ t = 1 T ( 1 P L M ( x ( t + 1 ) ∣ x ( t ) , . . . , x ( 1 ) ) ) 1 / T (5.5) \text{perplexity}=\prod_{t=1}^T\left(\frac1{P_{\rm LM}(x^{(t+1)}|x^{(t)},...,x^{(1)})}\right)^{1/T}\tag{5.5} perplexity=t=1∏T(PLM(x(t+1)∣x(t),...,x(1))1)1/T(5.5)
其实这是关于交叉熵损失函数的指数值:
= ∑ t = 1 T ( 1 y ^ x t + 1 ( t ) ) 1 / T = exp ( 1 T ∑ t = 1 T − log y ^ x t + 1 ( t ) ) = exp ( J ( θ ) ) (5.6) =\sum_{t=1}^T\left(\frac1{\hat y_{x_{t+1}}^{(t)}}\right)^{1/T}=\exp\left(\frac1T\sum_{t=1}^T-\log\hat y_{x_{t+1}}^{(t)}\right)=\exp(J(\theta))\tag{5.6} =t=1∑T(y^xt+1(t)1)1/T=exp(T1t=1∑T−logy^xt+1(t))=exp(J(θ))(5.6)
显然混乱度越低越好。
- 标准的语言模型评估指标是混乱度(perplexity):
notes
[notes (lectures 5 and 6)] 注意这是lecture5与lecture6共用
-
两种解决梯度消失的技术:notes p.8(这里其实已经涉及lecture6的内容,但是前面没有看到有用的东西,权当预习性质的记录一下)
- 矩阵初始化不使用随机初始化方法,而直接使用单位阵;
- 使用ReLU激活函数;
-
GRU:notes p.11-12
在此之前,我们先回顾一下标准RNN的传播形式(忽略截距项):
h t = σ ( W ( h h ) h t − 1 + W ( h x ) x t ) y ^ t = softmax ( W S h t ) (5.7) \begin{aligned} h_t&=\sigma(W^{(hh)}h_{t-1}+W^{(hx)}x_t)\\ \hat y_t&=\text{softmax}(W^{S}h_t) \end{aligned}\tag{5.7} hty^t=σ(W(hh)ht−1+W(hx)xt)=softmax(WSht)(5.7)
这里输入为一序列的单词 x 1 , . . . , x T x_1,...,x_T x1,...,xT(词向量),输出 y ^ ( t ) \hat y^{(t)} y^(t)是预测的序列中的一个结果。GRU的关键表达式如下所示:
z t = σ ( W ( z ) x t + U ( z ) h t − 1 ) Update gate r t = σ ( W ( r ) x t + U ( r ) h t − 1 ) Reset gate h ~ t = tanh ( r t ∘ U h t − 1 + W x t ) New memory h t = ( 1 − z t ) ∘ h ~ t + z t ∘ h t − 1 Hidden state (5.8) \begin{aligned} z_t&=\sigma(W^{(z)}x_t+U^{(z)}h_{t-1})&&\text{Update gate}\\ r_t&=\sigma(W^{(r)}x_t+U^{(r)}h_{t-1})&&\text{Reset gate}\\ \tilde h_t&=\tanh(r_t\circ Uh_{t-1}+Wx_t)&&\text{New memory}\\ h_t&=(1-z_t)\circ \tilde h_t+z_t\circ h_{t-1}&&\text{Hidden state} \end{aligned}\tag{5.8} ztrth~tht=σ(W(z)xt+U(z)ht−1)=σ(W(r)xt+U(r)ht−1)=tanh(rt∘Uht−1+Wxt)=(1−zt)∘h~t+zt∘ht−1Update gateReset gateNew memoryHidden state(5.8)
这里的 ∘ \circ ∘是一种门控运算,目前理解可能就是有一个阈值,一旦逾越就取零,否则就正常相乘。GRU门控机制说明:
- 新记忆生成:新记忆 h ~ t \tilde h_t h~t是由 h t h_t ht与 x t x_t xt线性组合构成,但是一旦被重置,应该就只剩下 tanh ( W x t ) \tanh(Wx_t) tanh(Wxt);
- 重置门:重置信号 r t r_t rt负责判定 h t − 1 h_{t-1} ht−1对新记忆 h ~ t \tilde h_t h~t到底有多重要,它可以直接抹去前面的所有记忆;
- 更新门:更新信号 z t z_t zt负责判定 h t − 1 h_{t-1} ht−1中有多少信息可以被传递到下一个隐层状态 h t h_t ht中,若 z ≈ 1 z\approx 1 z≈1,则 h t ≈ h t − 1 h_t\approx h_{t-1} ht≈ht−1;反之, h t h_t ht将基本由新记忆 h ~ t \tilde h_t h~t构成。
-
LSTM:notes p.13-14
关键表达式如下所示:
i t = σ ( W ( i ) x t + U ( i ) h t − 1 ) Input gate f t = σ ( W ( f ) x t + U ( f ) h t − 1 ) Forget gate o t = σ ( W ( o ) x t + U ( o ) h t − 1 ) Output/Exposure gate c ~ t = tanh ( W ( c ) x t + U ( c ) h t − 1 ) New memory cell c t = f t ∘ c t − 1 + i t ∘ c ~ t Final memory cell h t = o t ∘ tanh ( c t ) (5.9) \begin{aligned} i_t&=\sigma(W^{(i)}x_t+U^{(i)}h_{t-1})&&\text{Input gate}\\ f_t&=\sigma(W^{(f)}x_t+U^{(f)}h_{t-1})&&\text{Forget gate}\\ o_t&=\sigma(W^{(o)}x_t+U^{(o)}h_{t-1})&&\text{Output/Exposure gate}\\ \tilde c_t&=\tanh(W^{(c)}x_t+U^{(c)}h_{t-1})&&\text{New memory cell}\\ c_t&=f_t\circ c_{t-1}+i_t\circ \tilde c_t&&\text{Final memory cell}\\ h_t&=o_t\circ \tanh(c_t)&&\\ \end{aligned}\tag{5.9} itftotc~tctht=σ(W(i)xt+U(i)ht−1)=σ(W(f)xt+U(f)ht−1)=σ(W(o)xt+U(o)ht−1)=tanh(W(c)xt+U(c)ht−1)=ft∘ct−1+it∘c~t=ot∘tanh(ct)Input gateForget gateOutput/Exposure gateNew memory cellFinal memory cell(5.9)
同样地,这里的 ∘ \circ ∘运算符是LSTM中特殊的门控运算符,可以先理解为简单相乘。LSTM门控机制说明:
- 新记忆生成:这与GRU是类似的,即 c ~ \tilde c c~是由 x t x_t xt与 h t − 1 h_{t-1} ht−1线性组合得到的,但是这里并不会检验 h t − 1 h_{t-1} ht−1是否需要被遗忘,LSTM中是必然继承 h t − 1 h_{t-1} ht−1信息的;
- 输入门:使用 x t x_t xt与 h t − 1 h_{t-1} ht−1来判定输入是否值得被保留,即生成信号 i t i_t it来判定新记忆 c ~ t \tilde c_t c~t是否需要保留;
- 遗忘门:使用 x t x_t xt与 h t − 1 h_{t-1} ht−1来判定过去的记忆是否值得被保留,即生成信号 f t f_t ft来判定 c t − 1 c_{t-1} ct−1是否需要被保留;
- 输出门:这个相当于就是一个系数,在输入到下一个隐层 h t h_t ht时乘上即可;
suggested readings
- 主要关于n-gram模型的课本章节内容,值得注意的一个是其中提到了n-gram模型的smoothing,比如对于那些出现频次为零的文本可以默认频次都加一个常数,可能你会觉得即便这么做数据也是很不光滑的,文中还介绍了如拉普拉斯变换的smoothing手法。(N-gram Language Models)
- 介绍RNN应用的一篇博客,有趣的是其中的应用似乎是用C语言实现的。(The Unreasonable Effectiveness of Recurrent Neural Networks)
- 关于RNN的教材章节,感觉是一部非常不错的教材,详细阐述了RNN的原理、反向传播、梯度计算、变体、以及相关研究工作与应用。(Sequence Modeling: Recurrent and Recursive Neural Nets)
- 主要关于统计语言模型的一篇报告性质的博客,主要围绕大牛Noam Chomsky的工作展开。(On Chomsky and the Two Cultures of Statistical Learning)
assignment3 参考答案
[code] [handout] [latex template]
Assignment3参考答案(written+coding):囚生CYのGitHub Repository
1. Machine Learning & Neural Networks
-
( a ) (a) (a) 关于 Adam \text{Adam} Adam优化器(首次提出), PyTorch \text{PyTorch} PyTorch中的接口如下所示:
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)beta参数的两个值的正如第 ( 2 ) (2) (2)问中所示。-
( 1 ) (1) (1) 动量更新法则:保留当前点的信息(因为当前点的信息一定程度包含了之前所有更新迭代的信息,这有点类似LSTM与GRU的思想,但是此处并不会发生遗忘)
m ← β 1 m + ( 1 − β 1 ) ∇ θ J m i n i b a t c h ( θ ) θ ← θ − α m (a3.1.1) \begin{aligned} m&\leftarrow \beta_1 m+(1-\beta_1)\nabla_\theta J_{\rm minibatch}(\theta)\\ \theta&\leftarrow \theta-\alpha m \end{aligned}\tag{a3.1.1} mθ←β1m+(1−β1)∇θJminibatch(θ)←θ−αm(a3.1.1)
注意 β 1 \beta_1 β1的取值默认为 0.9 0.9 0.9,这表明会尽可能多地保留当前点的信息。从另一个角度来说,单纯的梯度下降法容易陷入局部最优,直观上来看,带动量的更新可以使得搜索路径呈现出一个弧形收敛的形状(有点像一个漩涡收敛到台风眼),因为每次更新不会偏离原先的方向太多,这样的策略容易跳出局部最优点,并且将搜索范围控制在一定区域内(漩涡内),容易最终收敛到全局最优。
-
( 2 ) (2) (2) 完整的 Adam \text{Adam} Adam优化器还使用了自适应学习率的技术:
m ← β 1 m + ( 1 − β 1 ) ∇ θ J m i n i b a t c h ( θ ) v ← β 2 v + ( 1 − β 2 ) ( ∇ θ J m i n i b a t c h ) ( θ ) ⊙ ∇ θ J m i n i b a t c h ( θ ) ) θ ← θ − α m / v (a3.1.2) \begin{aligned} m&\leftarrow \beta_1 m+(1-\beta_1)\nabla_\theta J_{\rm minibatch}(\theta)\\ v&\leftarrow\beta_2v+(1-\beta_2)(\nabla_\theta J_{\rm minibatch})(\theta)\odot\nabla_\theta J_{\rm minibatch}(\theta))\\ \theta&\leftarrow \theta-\alpha m/\sqrt{v} \end{aligned}\tag{a3.1.2} mvθ←β1m+(1−β1)∇θJminibatch(θ)←β2v+(1−β2)(∇θJminibatch)(θ)⊙∇θJminibatch(θ))←θ−αm/v(a3.1.2)
其中 ⊙ \odot ⊙与 / / /运算符表示点对点的乘法与除法(上面的 ⊙ \odot ⊙相当于是梯度中所有元素取平方)。β 2 \beta_2 β2默认值 0.99 0.99 0.99,这里相当于做了学习率关于梯度值的自适应调整(每个参数的调整都不一样,注意 / / /号是点对点的除法),在非稳态和在线问题上有很有优秀的性能。
一般来说随着优化迭代,梯度值会逐渐变小(理想情况下最终收敛到零),因此 v v v的取值应该会趋向于变小,步长则是变大,这个就有点奇怪了,理论上优化应该是前期大步长找到方向,后期小步长做微调。
找到一篇详细总结 Adam \text{Adam} Adam优化器优点的博客。
-
-
( b ) (b) (b) Dropout \text{Dropout} Dropout技术是在神经网络训练过程中以一定概率 p d r o p p_{\rm drop} pdrop将隐层 h h h中的若干值设为零,然后乘以一个常数 γ \gamma γ,具体而言:
h d r o p = γ d ⊙ h d ∈ { 0 , 1 } n , h ∈ R n (a3.1.3) h_{\rm drop}=\gamma d\odot h\quad d\in\{0,1\}^n,h\in\R^n\tag{a3.1.3} hdrop=γd⊙hd∈{0,1}n,h∈Rn(a3.1.3)
这里之所以乘以 γ \gamma γ是为了使得 h h h中每个点位的期望值不变,即:
E p d r o p [ h d r o p ] i = h i (a3.1.4) \mathbb E_{p_{\rm drop}}[h_{\rm drop}]_i=h_i\tag{a3.1.4} Epdrop[hdrop]i=hi(a3.1.4)-
( 1 ) (1) (1) 根据期望定义有如下推导:
E p d r o p [ h d r o p ] i = p d r o p ⋅ 0 + ( 1 − p d r o p ) γ h i = h i ⇒ γ = 1 1 − p d r o p (a3.1.5) \mathbb E_{p_{\rm drop}}[h_{\rm drop}]_i=p_{\rm drop}\cdot 0+(1-p_{\rm drop})\gamma h_i=h_i\Rightarrow\gamma=\frac1{1-p_{\rm drop}}\tag{a3.1.5} Epdrop[hdrop]i=pdrop⋅0+(1−pdrop)γhi=hi⇒γ=1−pdrop1(a3.1.5) -
( 2 ) (2) (2) Dropout \text{Dropout} Dropout是用来防止模型过拟合,缓解模型运算复杂度,评估的时候显然不能使用 Dropout \text{Dropout} Dropout,因为用于评估的模型必须是确定的, Dropout \text{Dropout} Dropout是存在不确定性的。
-
2. Neural Transition-Based Dependency Parsing
本次使用的是 PyTorch1.7.1 \text{PyTorch1.7.1} PyTorch1.7.1 CPU \text{CPU} CPU版本,当然使用 GPU \text{GPU} GPU版本应该会更好。
本次实现的是基于 Transition \text{Transition} Transition的依存分析模型,就是在实现[notes]中的Greedy Deterministic Transition-Based Parsing算法。其中SHIFT是将缓存中的第一个移入栈,LEFT-ARC与RIGHT-ARC分别是建立栈顶前两个单词之间的依存关系。
-
( a ) (a) (a) 具体每步迭代结果如下所示(默认ROOT是指向parsed的):
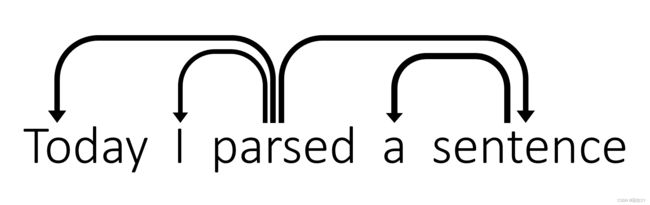
Stack Buffer New dependency Transition [ROOT] [Today, I, parsed, a, sentence] Initial Configuration [ROOT, Today] [I, parsed, a, sentence] SHIFT [ROOT, Today, I] [parsed, a, sentence] SHIFT [ROOT, Today, I, parsed] [a, sentence] SHIFT [ROOT, Today, parsed] [a, sentence] parsed → \rightarrow → I LEFT-ARC [ROOT, parsed] [a, sentence] parsed → \rightarrow → Today LEFT-ARC [ROOT, parsed, a] [sentence] SHIFT [ROOT, parsed, a, sentence] [] SHIFT [ROOT, parsed, sentence] [] sentence → \rightarrow → a LEFT-ARC [ROOT, parsed] [] parsed → \rightarrow → sentence RIGHT-ARC [ROOT] [] ROOT → \rightarrow → parsed RIGHT-ARC -
( b ) (b) (b) SHIFT共计 n n n次,LEFT-ARC与RIGHT-ARC合计 n n n次,共计 2 n 2n 2n次。
-
( c ) (c) (c) 非常简单的状态定义与转移定义代码实现,运行
python parser_transitions.py part_c通过测试。 -
( d ) (d) (d) 运行
python parser_transitions.py part_d通过测试。 -
( e ) (e) (e) 实现神经依存分析模型,参考的是lecture4推荐阅读的第二篇(A Fast and Accurate Dependency Parser using Neural Networks)。运行
python run.py通过测试。注意这一题要求是自己实现全连接层和嵌入层的逻辑,不允许使用PyTorch内置的层接口,有兴趣的自己去实现吧,我就直接调用接口了。如果是要从头到尾都重写,这个显得就很困难(需要把反向传播和梯度计算的逻辑都要实现),然而本题的模型还是继承了
torch.nn.Module的,因此似乎只能继承torch.nn.Module写自定义网络层,这样其实还是比较简单的,这可以参考我的博客2.1节的全连接层重写的代码。运行结果:
================================================================================ INITIALIZING ================================================================================ Loading data... took 1.36 seconds Building parser... took 0.82 seconds Loading pretrained embeddings... took 2.48 seconds Vectorizing data... took 1.22 seconds Preprocessing training data... took 30.56 seconds took 0.02 seconds ================================================================================ TRAINING ================================================================================ Epoch 1 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:18<00:00, 23.61it/s] Average Train Loss: 0.18908768985420465 Evaluating on dev set 1445850it [00:00, 46259788.38it/s] - dev UAS: 83.75 New best dev UAS! Saving model. Epoch 2 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:15<00:00, 24.52it/s] Average Train Loss: 0.1157231591158099 Evaluating on dev set 1445850it [00:00, 92527340.72it/s] - dev UAS: 86.22 New best dev UAS! Saving model. Epoch 3 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:14<00:00, 24.86it/s] Average Train Loss: 0.1010169279418918 Evaluating on dev set 1445850it [00:00, 61690227.55it/s] - dev UAS: 87.04 New best dev UAS! Saving model. Epoch 4 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:16<00:00, 24.17it/s] Average Train Loss: 0.09254590892414381 Evaluating on dev set 1445850it [00:00, 46221356.67it/s] - dev UAS: 87.43 New best dev UAS! Saving model. Epoch 5 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:16<00:00, 24.06it/s] Average Train Loss: 0.08614181549977754 Evaluating on dev set 1445850it [00:00, 46262964.50it/s] - dev UAS: 87.72 New best dev UAS! Saving model. Epoch 6 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:19<00:00, 23.20it/s] Average Train Loss: 0.08176740852599859 Evaluating on dev set 1445850it [00:00, 46264729.20it/s] - dev UAS: 88.29 New best dev UAS! Saving model. Epoch 7 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:17<00:00, 23.95it/s] Average Train Loss: 0.07832196695343047 Evaluating on dev set 1445850it [00:00, 45695793.40it/s] - dev UAS: 88.17 Epoch 8 out of 10 100%|██████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:15<00:00, 24.40it/s] Average Train Loss: 0.07501755065982153 Evaluating on dev set 1445850it [00:00, 46264729.20it/s] - dev UAS: 88.53 New best dev UAS! Saving model. Epoch 9 out of 10 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:16<00:00, 24.15it/s] Average Train Loss: 0.07205055564545192 Evaluating on dev set 1445850it [00:00, 45701992.11it/s] - dev UAS: 88.47 Epoch 10 out of 10 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1848/1848 [01:15<00:00, 24.54it/s] Average Train Loss: 0.06958463928537258 Evaluating on dev set 1445850it [00:00, 46266141.05it/s] - dev UAS: 88.76 New best dev UAS! Saving model. ================================================================================ TESTING ================================================================================ Restoring the best model weights found on the dev set Final evaluation on test set 2919736it [00:00, 92289480.94it/s] - test UAS: 89.15 Done!作业中提到训练需要一个小时,使用 GPU \text{GPU} GPU可以大大加快速度,训练过程中的损失函数值与 UAS \text{UAS} UAS指数全部达标。(损失函数值应当低于 0.2 0.2 0.2, UAS \text{UAS} UAS超过 87 % 87\% 87%)
-
( f ) (f) (f) 这里提到几种解析错误类型:
- 介词短语依存错误: sent into Afghanistan \text{sent into Afghanistan} sent into Afghanistan中正确的依存关系是 sent → Afghanistan \text{sent}\rightarrow\text{Afghanistan} sent→Afghanistan
- 动词短语依存错误: Leaving the store unattended, I went outside to watch the parade \text{Leaving the store unattended, I went outside to watch the parade} Leaving the store unattended, I went outside to watch the parade中正确的依存关系是 went \text{went} went指向 leaving \text{leaving} leaving
- 修饰语依存错误: I am extremely short \text{I am extremely short} I am extremely short中正确的依存关系是 short → extremely \text{short}\rightarrow\text{extremely} short→extremely
- 协同依存错误: Would you like brown rice or garlic naan \text{Would you like brown rice or garlic naan} Would you like brown rice or garlic naan中短语 brown rice \text{brown rice} brown rice和 garlic naan \text{garlic naan} garlic naan是并列的,因此 rice \text{rice} rice应当指向 naan \text{naan} naan
下面几小问不是那么确信,将就着看吧。
-
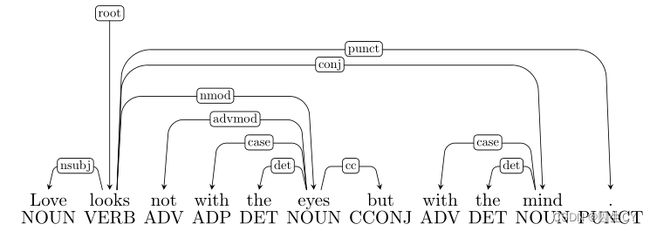
( 1 ) (1) (1) 这个感觉是介词短语依存错误,但是 looks \text{looks} looks的确指向 eyes \text{eyes} eyes和 mind \text{mind} mind了,这是符合上面的说法的。难道是协同依存错误?
-
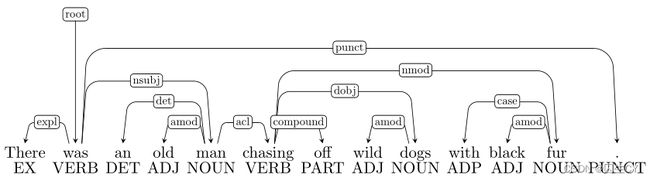
( 2 ) (2) (2) 这个感觉还是介词短语依存错误: chasing \text{chasing} chasing不该指向 fur \text{fur} fur, fur \text{fur} fur应该是与 dogs \text{dogs} dogs相互依存。
-
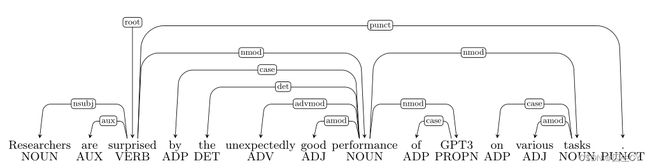
( 3 ) (3) (3) 这个很简单是 unexpectedly \text{unexpectedly} unexpectedly和 good \text{good} good之间属于修饰语依存错误,应当由 good \text{good} good指向 unexpectedly \text{unexpectedly} unexpectedly;
-
( 4 ) (4) (4) 这个根据排除法(没有介词短语,没有修饰词,也没有并列关系)只能是动词短语依存错误,但是具体是哪儿错了真的看不出来,可能是 crossing \text{crossing} crossing和 eating \text{eating} eating之间错标成了协同依存关系?
lecture 6 梯度消失与爆炸,变体RNN,seq2seq
slides
[slides]
-
RNN中的梯度消失问题:slides p.21-30
梯度消失在RNN中是最为常见的,因为RNN中容易包含一个很长很长的传播链。
我们继续用下面这张图来说明梯度消失:
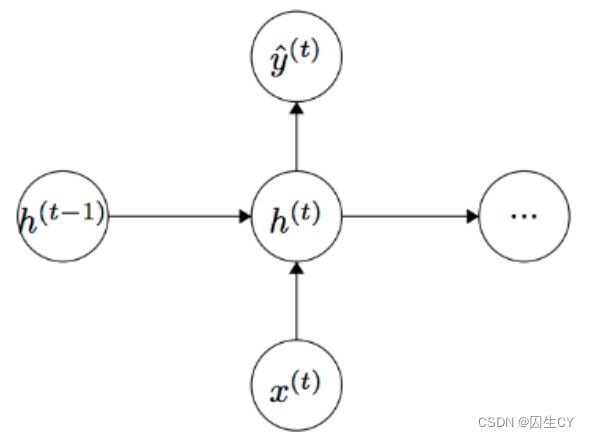
RNN神经网络传播的数学表达式:
< f o n t f a c e = t i m e s n e w r o m a n > h ( t ) = σ ( W h h ( t − 1 ) + W x x ( t ) + b 1 ) < / f o n t > (6.1) h^{(t)}=\sigma(W_hh^{(t-1)}+W_xx^{(t)}+b_1)\tag{6.1} <fontface=timesnewroman>h(t)=σ(Whh(t−1)+Wxx(t)+b1)</font>(6.1)
为了便于求导,假定激活函数 σ ( x ) = x \sigma(x)=x σ(x)=x,即不作激活,有如下推导:
< f o n t f a c e = t i m e s n e w r o m a n > ∂ h ( t ) ∂ h ( t − 1 ) = diag ( σ ′ ( W h h ( t − 1 ) + W x x ( t ) + b 1 ) ) W h = I W h = W h < / f o n t > (6.2) \frac{\partial h^{(t)}}{\partial h^{(t-1)}}=\text{diag}(\sigma'(W_hh^{(t-1)}+W_xx^{(t)}+b_1))W_h=IW_h=W_h\tag{6.2} <fontface=timesnewroman>∂h(t−1)∂h(t)=diag(σ′(Whh(t−1)+Wxx(t)+b1))Wh=IWh=Wh</font>(6.2)
考察第 i i i次循环输出的损失 J ( i ) ( θ ) J^{(i)}(\theta) J(i)(θ)相对于第 j j j个隐层 h ( j ) h^{(j)} h(j)的梯度(令 l = i − j l=i-j l=i−j):
< f o n t f a c e = t i m e s n e w r o m a n > ∂ J ( i ) ( θ ) ∂ h ( j ) = ∂ J ( i ) ( θ ) ∂ h ( i ) ∏ t = i + 1 j ∂ h ( t ) ∂ h ( t − 1 ) = ∂ J ( i ) ( θ ) ∂ h ( i ) ∏ t = i + 1 j W h = ∂ J ( i ) ( θ ) ∂ h ( i ) W h l < / f o n t > \frac{\partial J^{(i)}(\theta)}{\partial h^{(j)}}=\frac{\partial J^{(i)}(\theta)}{\partial h^{(i)}}\prod_{t=i+1}^j\frac{\partial h^{(t)}}{\partial h^{(t-1)}}=\frac{\partial J^{(i)}(\theta)}{\partial h^{(i)}}\prod_{t=i+1}^jW_h=\frac{\partial J^{(i)}(\theta)}{\partial h^{(i)}}W_h^l <fontface=timesnewroman>∂h(j)∂J(i)(θ)=∂h(i)∂J(i)(θ)t=i+1∏j∂h(t−1)∂h(t)=∂h(i)∂J(i)(θ)t=i+1∏jWh=∂h(i)∂J(i)(θ)Whl</font>
若 W h W_h Wh不满秩(如 W h W_h Wh是稀疏矩阵),则随着 W h W_h Wh的求幂会使得 W h W^h Wh的秩越来越小,最后就会变成一个零矩阵,这就是梯度消失。事实上对于一般的非线性激活函数 σ \sigma σ,梯度消失的问题总是存在,ReLU是为解决梯度消失问题而提出的一种分段激活函数。
对于RNN来说,梯度消失意味着的记忆完全损失,类似GRU中彻底遗忘过去的记忆,对于长文本中间隔较长的上下文单词就很难建立联系。
不过某种意义上,在一些人眼中梯度消失并未必是坏事,这对于大模型来说,梯度消失一定程度上指示了模型优化的方向,即可以移除那些不必要的神经元。
-
梯度爆炸:slides p.31-32
梯度爆炸带来的直接问题就是梯度下降法中步长过大,从而错过全局最优点。在模型训练中有时候你发现损失函数突然蹦出一个Inf或者NaN,这很有可能是发生了梯度爆炸(你可以从之前的checkpoint中调取模型重新训练)。
梯度爆炸直接的解决方案就是限制梯度的大小,超过一定阈值就对梯度进行放缩。
-
**解决RNN梯度消失问题(LSTM与GRU):**slides p.33-41
关于LSTM与GRU的原理公式解析详见lecture5中notes小节的内容。
LSTM与GRU的门控机制使得更容易保留长距离之前的记忆,因而解决了梯度消失可能导致的问题。比如设置遗忘门的信号值为 1 1 1,输入门的信号值为 0 0 0,则过去的信息将会无限制地被保留下来。但是LSTM并不确保一定不会发生梯度消失或梯度爆炸的问题,它只是提供了一种保留长距离依赖的方法,并非彻底解决梯度消失。
LSTM通常是最好的选择,尤其在数据很多且存在长距离依赖的情况;GRU的优势在于运算更快。但是目前的趋势是RNN逐渐被Transformer取代。
-
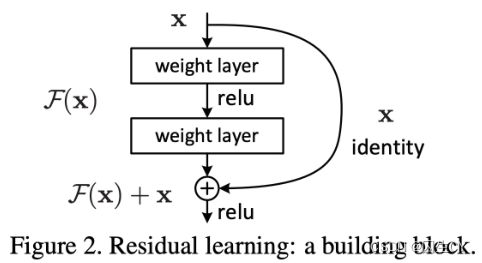
残差链接(residual connections):slides p.42
梯度消失并不只是会在RNN中出现,在任何大模型中都很容易出现,因此需要引入残差连接。
即将距离较长的两个神经元直接相连,以避免梯度消失( F ( x ) + x F(x)+x F(x)+x求导,在 F ( x ) F(x) F(x)导数为零的情况下,依然可以得到 1 1 1,因而避免了梯度消失)。
其他用以解决梯度消失与梯度爆炸问题的方法:
① DenseNet:将每一层都与后面的层相连接;
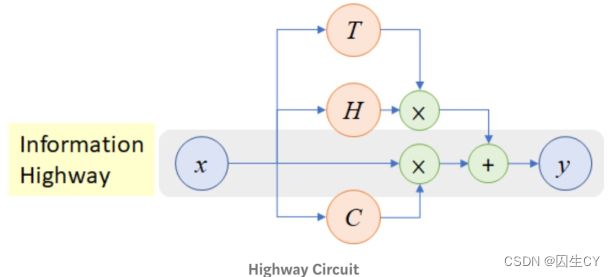
② HighWay:类似残差连接,但是引入了一个动态的门控机制进行控制:
-
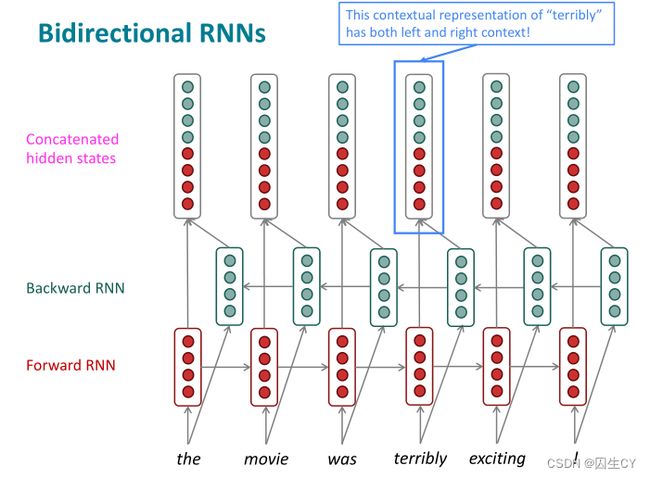
双向RNN与多层RNN:slides p.44-51
双向RNN非常容易理解,即正着遍历一次输入序列得到一个正向RNN的输出序列,反着再遍历一次序列,得到反向RNN的输出序列,然后将两个输出序列对应节点进行运算(一般是直接拼接即可)输出得到最终的输出序列,下面这个图就讲得非常清楚:
注意双向RNN仅在整个序列可知的情况下才能使用(此时双向RNN将会非常强大,比如BERT模型就是建立在双向RNN上的),比如在语言模型中就不能使用,因为语言模型中只有左侧一边的文本序列。
多层RNN就更容易理解了,即将RNN的输出序列作为输入序列输入到下一个RNN中。实际应用中Massive Exploration of Neural Machine Translation Architecutres指出在神经机器翻译中,2~4层的RNN编码器结构是最优的,4层的RNN解码器是最优的。且一般情况下残差连接与稠密连接(dense connections)对于多层RNN是非常必要的(如8层的RNN)。
基于Transformer的网络(如BERT)的网络深度会更高(通常有12层或24层)。
notes
[notes (lectures 5 and 6)] 注意这是lecture5与lecture6共用
详见lecture5的notes小节内容。
suggested readings
- 这个就是lecture5推荐阅读的第三篇,即那本写得很好的教材中的RNN章节。(Sequence Modeling: Recurrent and Recursive Neural Nets)
- 截至本文发布,这篇文献的链接挂掉了,我从百度学术另外找了个Citeseer的下载链接,这篇就更老了,是1994年的老古董,它可能是最早提出梯度消失概念的文献之一。(Learning long-term dependencies with gradient descent is difficult)
- 2012年上传于ARXIV的一篇关于RNN中梯度消失以及梯度爆炸造成的训练困难问题,以及提出的解决方案,内容比较基础过时。(On the difficulty of training Recurrent Neural Networks)
- 用以解释梯度消失问题的JupyterNotebook。(Vanishing Gradients Jupyter Notebook)
- 讲解LSTM模型的一篇博客。(Understanding LSTM Networks)