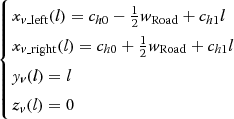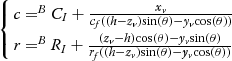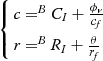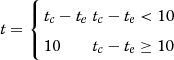Real-time lane departure warning system based on a single FPGA

Real-time lane departure warning system based on a single FPGA

• Xiangjing An,
• Erke ShangEmail author,
• Jinze Song,
• Jian Li and
• Hangen He

EURASIP Journal on Image and Video Processing20132013:38

DOI: 10.1186/1687-5281-2013-38

©  An et al.; licensee Springer. 2013

Received: 8 October 2012

Accepted: 7 June 2013

Published: 4 July 2013

Abstract

Abstract

This paper presents a camera-based lane departure warning system implemented on a field programmable gate array (FPGA) device. The system is used as a driver assistance system, which effectively prevents accidents given that it is endowed with the advantages of FPGA technology, including high performance for digital image processing applications, compactness, and low cost. The main contributions of this work are threefold. (1) An improved vanishing point-based steerable filter is introduced and implemented on an FPGA device. Using the vanishing point to guide the orientation at each pixel, this algorithm works well in complex environments. (2) An improved vanishing point-based parallel Hough transform is proposed. Unlike the traditional Hough transform, our improved version moves the coordinate origin to the estimated vanishing point to reduce storage requirements and enhance detection capability. (3) A prototype based on the FPGA is developed. With improvements in the vanishing point-based steerable filter and vanishing point-based parallel Hough transform, the prototype can be used in complex weather and lighting conditions. Experiments conducted on an evaluation platform and on actual roads illustrate the effective performance of the proposed system.

1 Introduction

Automobile accidents injure between 20 to 50 million people and kill at least 1.2 million individuals worldwide each year [1]. Among these accidents, approximately 60% are due to driver inattentiveness and fatigue. Such accidents have prompted the development of many driver assistance systems (DASs), such as the onboard lane departure warning systems (LDWSs) and forward collision warning systems. These systems can prevent drivers from making mistakes on the road and can reduce traffic accidents. An effective DAS should satisfy the following requirements: accuracy, reliability, robustness, low cost, compact design, low dissipation, and applicability in real time, etc. Therefore, a personal computer, for example, is not suitable for the DAS platform because of its high cost and large size.

Nowadays, dozens of LDWSs are proposed and exist in the market place. These LDWSs are based on some different kinds of platforms. However, complex environments make LDWS applications difficult. Therefore, many of these systems are used only on highways, and they typically suffer from defective operation under rainy or under heavy shadows.

To enhance the performance of current LDWSs under complex conditions, we implemented improvements in edge extraction and line detection. In the edge extraction step, we use the vanishing point to guide the orientation of edge pixels, thereby enhancing LDWS performance under heavy shadows. We choose the Hough transform and develop its capability in the line detection step. Using the information of vanishing point, the space complexity of the Hough transform is greatly reduced. These two improvements enable our system to work effectively under most lighting and weather conditions.

The remainder of this paper is organized as follows. Section 2 discusses some related works about edge extraction and line detection, especially the limitation of traditional Hough transform. Section 3 discusses the proposed hardware architecture of the LDWS and the workflow of each of its parts. Section 4 describes the vanishing point-based steerable filter and its implementation on a field programmable gate array (FPGA) device. Section 5 presents the improved vanishing point-based parallel Hough transform, including technical details and results. In Section 6, we theoretically and experimentally analyze the distribution of vanishing points. The influence of curves is also discussed in this section. Section 7 illustrates the details of the system and the results of on-road experiments. Section 8 concludes the paper.

2 Related works

Lane detection is a key task of the LDWS. However, it is a difficult problem due to the complex environments. In addition, the single FPGA platform prevents many classical algorithms such as Canny or improved Canny algorithms from satisfying computing resources and storage requirements. In this section, we mainly focus on improving the edge extraction and line detection algorithm to develop our LDWS to be more robust and effective.

2.1 Edge extraction algorithms

In order to detect lane robustly, one of the key aspects is edge extraction. Over 2 decades of research, many edge enhancement algorithms have been proposed [2]. Canny algorithm and improved Canny algorithms are thought to be most effective under common environments [3]. But their computing complexities limit their application on embedded platforms.

Recently, an algorithm named steerable filters is used in edge extraction [1, 4–6]. Its effect depends on the accuracy of the lane orientation. In [4] and [1], researchers analyzed the orientation of local features at each pixel and used this orientation as the direction. This approach is useful in most cases but results in poor performance when lane marking boundaries are not dominant under complex shadows. In [5], the detected angle of a lane in the pre-frame stage is chosen, but angle detection is characterized by errors when vehicles change lanes. For making the problem easier, Anvari [6] divided the image into several windows. In each window, a fixed direction was chosen for the steerable filter.

To improve the effectiveness of edge extraction, we developed and implemented an algorithm, which we call the vanishing point-based steerable filter, on an FPGA device. By estimating the vanishing point position in the next frame of an image, the orientation at each pixel is computed under the guide of the vanishing point. Therefore, compared to previous algorithms, the result of our algorithm is much improved.

2.2 Line detection algorithms

Line detection is deemed the most important component of LDWSs. Numerous line detection algorithms and techniques have recently been proposed [ 7– 12]. Among these algorithms, the Hough transform is one of the most robust and extensively used [ 13– 17].The Hough transform is implemented according to (1):

ρ=xcos(θ)+ysin(θ)

(1)

The main drawbacks of this algorithm are its considerable requirements for memory and computational time [18]. Compared to personal computers, the embedded platform is much more sensitive to the usage of memory and computational resources. Therefore, the traditional Hough transform is almost impossible to apply in embedded platforms.

To solve these problems, researchers have made many improvements to the Hough transform. Chern et al. presented a parallel Hough transform to reduce execution time [18]. However, its space complexity remains. A line segment detection system was also developed using the parallel Hough transform on FPGAs, but the same problem of resources needed prevents most type of FPGAs [13]. For the same reason, Hough transform technologies were discarded by Marzotto [19], whose work is also researching an LDWS on a single chip.

To reduce the space complexity, Mc Donald [20] hypothesized an implicit constraint region of the vanishing point position during the Hough transform, but he did not provide details on how to design the constraint region and its size in relation to curved roads.

In this paper, we use the vanishing point as a guide to decrease the Hough transform’s space complexity. Unlike the traditional Hough transform, our improved version moves the coordinate origin of the Hough transform to the estimated vanishing point. Thus, each lane marking crosses the Hough transform coordinate origin. In this ideal case, it only needs to store the parameter where ρ=0. These lines that do not cross the vanishing point are disregarded. This is the main reason our improved Hough transform can reduce the storage space and improve the detection performance.

3 Hardware architecture of LDWS

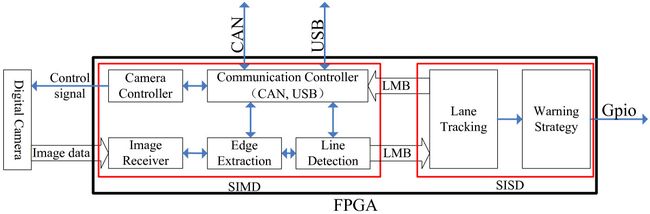
Dozens of LDWSs are proposed or exist in the market place today. Among these platforms, personal computers, microprocessors, and DSPs are based on single instruction single data (SISD) structures. On the other hand, the single instruction multiple data (SIMD) structure is designed in [19, 21, 22]. It is obvious that the SISD structure is flexible for symbol operations but has low capability for large data streams. By contrast, the SIMD structure is highly efficient for large data stream with simple operations, but low capability for complex operations. In order to possess of both efficiency the large data stream operations and flexibility for symbol operations, Hsiao et al. presented an FPGA + ARM (Advanced RISC Machines) architecture of their LDWS [23]. In the FPGA, an SIMD structure is designed for preprocessing. Complex operations are finished in the ARM, which is based on the SISD structure. We agree that an SIMD + SISD hardware architecture is effective to visual process. To reduce the size, cost, and complexity of that hardware architecture, we implemented it on a single FPGA chip. A MicroBlaze soft core, which is embedded in the FPGA chip, is chosen instead of the ARM chip in our LDWS.

Our LDWS is composed of several units (Figure  1)  camera control,  image receiver,  edge extraction,  line detection,  lane tracking,  warning strategy, and  external communication control units.

Figure 1

The structure of LDWS. The architecture of the proposed LDWS.

3.1 SIMD + SISD architecture

Lane detection warning is a typical computer vision process. Analyzing the relationship between data streams and information included in this data stream, we divide the vision process into two levels: the data process level and the symbol process level. The vision tasks in the data process level are characterized by a large data stream with simple operations, such as convolution, edge extraction, and line detection. By contrast, the vision tasks in the symbol process level are characterized by a small data stream with complex operations.

Hence, two parts of different computational structures are specially designed to process these two kinds of vision tasks (Figure 1). The computational structure for the data process is based on a SIMD structure that comprises specialized vision processing engines synthesized by the hardware description language (HDL). The other structure is based on a SISD structure that consists of an embedded MicroBlaze soft core, which is offered by Xilinx for free.

The SIMD + SISD architecture has two advantages: first, these vision processing engines are specially designed and efficiently handle data process vision tasks. Second, MicroBlaze is considerably more flexible than processing engines, making these algorithms easy to implement. It also improves complex algorithms and enables the convenient incorporation of new functions.

3.2 The flow of our system

The function, input and output sequences, and internal operations of the system are discussed as follows.

3.2.1 Camera controller unit

Our system uses a digital camera. In the camera controller unit, the automatic exposure control algorithm proposed by Pan et al. is implemented [24]. Some parameters, such as exposure time and gain, are sent to the camera by serial peripheral interface bus. The others represent the camera’s enable signal and required frame signal, among others.

3.2.2 Image receiver unit

This unit receives image data from the digital camera under line synchronic and frame synchronic signals. Eight-bit gray data are transmitted to the FPGA based on a 40-MHz camera clock.

3.2.3 Edge extraction unit

This unit extracts an edge image from the original image using the vanishing point-based steerable filter. We use high-level information (the vanishing point) to obtain the orientation of the local features at each pixel. During edge extraction, each potential edge pixel of the lane should be directed toward the vanishing point. The details of this algorithm and its implementation on the FPGA are described in Section 4.

The image receiver unit uses the 8-bit original image data, data enabling signal, and synchronic clock as input; the output are the 1-bit edge image data, data enabling signal, and synchronic clock.

3.2.4 Line detection unit

In this unit, a vanishing point-based parallel Hough transform is designed and implemented for line detection. When the edge image is extracted by the edge extraction unit, a BlockRAM registers the position of a series of edge points. The edge image is unsuitable for calculation via a line equation because this equation requires x and y coordinates. The edge image, on the other hand, uses only binary information. We therefore store a list of edge positions instead of the edge image. To reduce computational complexity, we implement a parallel Hough transform [18] in this unit. We move the coordinate origin of the Hough transform to the estimated vanishing point to reduce space complexity. During the Hough transform process, a series of double-port BlockRAM are used as parameter storage. Details on the line detection algorithm and its implementation on the FPGA are described in Section 4.

This unit employs the 1-bit edge image data, data enabling signal, and synchronic clock as input; the output is a list of line position parameters.

3.2.5 Lane tracking unit

The lane tracking unit and the warning strategy unit are implemented in an embedded MicroBlaze soft core. A pair of local memory buses are used to exchange these parameters between MicroBlaze and other units. A series of rules are set to remove disturbance lines, such as the vanishing point constraint and slope constraint. A simple algorithm similar to the Kalman filter is implemented for stable lane tracking.

This unit employs a series of line parameters as input; the output is a pair of final lane parameters.

3.2.6 Warning strategy unit

When double lanes are found, coordinate transform is carried out to determine the relationship between lanes and vehicle wheels. If a wheel crosses a lane, a warning message is sent.

3.2.7 Communication controller unit

For easy and thorough system debugging and operation, we designed a controller area network (CAN) bus and a universal serial bus (USB). The USB is used primarily to debug the algorithm; an example is that the processed data is transmitted to a computer for debugging. The processed data include the original image data, edge image data, and all the line position parameters detected by our improved Hough transform. Therefore, testing our algorithms in the FPGA device is a convenient process. The CAN bus is used mainly for receiving vehicle information (because CAN bus is widely used in vehicles), such as vehicle velocity and indicator information. The CAN bus is also used to send out warning signals from the LDWS, including those lane position parameters, distance between vehicles and lanes, and time spent crossing a lane. In addition, the CAN bus is used to enter the user’s command instructions.

4 Edge extraction using the vanishing point-based steerable filter

In this section, we use the estimated vanishing point to develop the effectiveness of the steerable filter. The details on the implementation of the proposed algorithm on the FPGA device are also presented.

4.1 Vanishing point-based steerable filter

The core principle of the steerable filter is that a Gaussian filter in any orientation can be synthesized by a set of basic Gaussian filters [ 25]. This principle can be expressed by:

Rθ=cos(θ)R0∘+sin(θ)R90∘

(2)

where  R0∘=I∗G0∘ 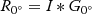,  R90∘=I∗G90∘ 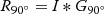, and I means the original image;  G0∘  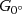and  G90∘  are a pair of basic filters, and ∗represents the convolution operation. Therefore, the filter result of the θ orientation can be synthesized using the results of each basic filter.

The effect of the steerable filter on edge extraction depends on the accuracy of the lane orientation. Common edge detectors identify the local maxima of intensity changes as the orientation [1, 4]. Occasionally, however, boundary lane markings may not be as dominant as other road features under shadows. The local features of lane markings follow a clear global distribution pattern in road scene images. We prefer identifying the local edges at each pixel location according to the high-level information (vanishing point) on the lane markings. A local edge extraction algorithm, called the vanishing point-based steerable filter, is proposed. The implementation of the algorithm is summarized as follows.

Input: digital image of the road scene, the estimated vanishing point.

Output: binary image containing edge points bw.

Step1: The desired direction at each pixel is calculated according to the estimated vanishing point. A digital image called the direction map (Figure  2b) is then obtained at the same size as that of the input image. The range of direction is [-pi, pi].

Figure 2

The process of the vanishing point-based steerable filter. The process of the vanishing point-based steerable filter. (a) is the original image, and (b) is the direction map decided by the estimated vanishing point. (c) and (d) are the response image convoluted by  G0∘ 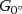 and  G90∘ 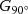. (e) is the result of rising (red) and falling (green) edges synthesized by (c) and (d). (f) is the final binary image of matching the rising and falling edges. (g) and (i) are the result of Sobel algorithm and Canny algorithm. (h)and (j) are the result of matching both rising edges and falling edges of (g) and (i).

Step2: A pair of basic filters,  G0∘ 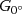 and  G90∘  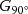are used to convolve the input image and obtain response images, respectively. The results are shown in Figure 2c,d.

Step3: The result of all pixels are obtained according to the direction map, as shown in Figure 2e. This result is a linear combination of the results for basic filters.

Step4: The rising and falling edges are mapped, and the final binary image bw (Figure 2f) is obtained. We then return tobw.

Figure 2 shows the process involved in our edge extraction algorithm. Estimating the vanishing point yields the orientation at each pixel (Figure 2b). At the same time, a pair of basic filters is convolved with the original image. The results are shown in Figure 2c,d. Using the orientation map as reference, we synthesize (c) and (d) into (e). In Figure 2e, the red points denote the rising edges, and the green points represent the falling edges. Figure 2f shows the final result of matching the rising and falling edges.

4.2 Implementation on an FPGA device

The steerable filter is advantageous in that basic filters can work independently on an FPGA device. The proposed framework in our system is designed in a pipeline and in parallel. It is combined by two parts: a couple of basic filters and the coefficients for synthesizing results into a final outcome. The steerable filter can generally be arranged in any order, depending on the number of basic filters. The basic set of filters is easy to express in discrete form from a 2D Gaussian function: an  n ×  m matrix. All digital data are pipelined on the structure under the control clock (Figure  3a). At each clock,  n ×  m adjacent pixels are chosen to complete a couple of convolution operations. Therefore, convolution is completed during the arrival of the original data, and no extra computational time is spent.

Figure 3

The architecture of the vanishing point-based steerable filter implemented on FPGA. The architecture of the proposed filter implemented on FPGA. (a) is the structure of convolution operation. (b) is the structure of synthesizing the results from basic filters into the final result according to orientations at each pixel. DP means data position, and VP means vanishing point position. CODIC IP core is used to compute the orientation at each pixel.

The same number of engines is used to complete the convolutions of all the basic filters. With different coefficients in the convolution operation, the results of these basic filters are simultaneously generated as shown in Figure 3b.

Figure  3 shows the core function of the proposed algorithm. Its time and resource cost is listed in Table  1. CC in Table  1means camera control model, and EE means edge extraction model. We can see that by adding the proposed filter, almost no external time is needed, and its resource cost is also very low.

Table 1

Time and resources occupation of the proposed LDWS

	Module	CC	CC + EE	CC + EE + VPPHT	CC + EE + VPPHT + TRW
	Time (ms) (average)	9.24	9.32	13.92	25
Resource	Total LUTs	1,944 (4%)	2,901 (6%)	4,632 (9.7%)	8,793 (18%)
	Flip flops	2,936 (6%)	3,762 (7.8%)	4,966 (10%)	7,085 (15%)
	Block RAM	0	6 (5%)	46 (37%)	110 (87%)
	DSP48	3(2%)	5 (4%)	21 (16%)	25 (19%)

The effectiveness of the proposed algorithm is also shown in Figure 2. Traditional Sobel algorithm and Canny algorithm are used as comparison. The results of Sobel algorithm and Canny algorithm generated by Matlab tool (version 7.5.0) are shown in Figure 2g,i. Figure 2h,j shows the results of mapping rising and falling edges. Apparently, Sobel algorithm lost the middle lane marking. Though all of the lane markings are detected by Canny algorithm, there are more pixels out of lanes remain. These remaining pixels would not only increase the computing complexity but also disturbs the real lane detection.

5 Using the vanishing point to reduce parallel Hough transform space complexity

In [18], a parallel Hough transform for reducing execution time was proposed, but space complexity remains. In this section, we introduce the basic principle of the parallel Hough transform and the vanishing point-based parallel Hough transform. Moving the coordinate origin to the vanishing point considerably reduces the space complexity presented by the Hough transform. The control experiment shows that the improved Hough transform efficiently reduces space complexity. Finally, a new constraint generated by the improved Hough transform is imposed on line detection.

5.1 Parallel hough transform

The core principle of the parallel Hough transform is to divide the range of  θ into  n pieces, using  n processing engines to separately calculate  ρ. The structure of the parallel Hough transform is shown in Figure  4. First, the edge information on each point in the edge image is stored in a BlockRAM. The range of  θ is divided into  n intervals. In each  θ interval, a set of pipeline process elements are designed for the Hough transform, including calculation, voting, and peak detection, where the processing engine module is specially designed for calculating  ρ according to (1). In each pipeline, only one peak is detected as a candidate. The lane candidates are estimated, filtered, and tracked in the lane tracking unit.

Figure 4

The workflow of the parallel Hough transform. The workflow of the parallel Hough transform. The range of θ is divided into npieces. n processing engines are working in parallel. In each processing engine, a set of pipeline process elements are designed to execute the Hough transform operation.

Our system shows an implicit constraint on peak detection. As the angle is divided into n intervals, the number of lanes in each interval is one, at most. This result indicates that only one maximum value is needed as a candidate line in each angle interval.

The peak detection method in our algorithm also slightly differs from that in traditional methods. The dual-port RAM is used for memory storage. For each θ i , ρ i is computed according to (1). First, voting value d(θ i , ρ i ) is read out from a cell (θ i ,ρ i ), as is done in traditional methods. A compare operation is implemented before writing voting value d(θ i , ρi ) + 1 back into the same memory cell. The purpose of the compare operation is to determine whether the current voting value is the maximum in that voting memory. The read and write operations are separately implemented on the rising edge and falling edge of each clock period. The compare operation is performed during the clock holding time. Hence, the voting operation can be implemented within one-clock period. Peak detection is completed during the voting operation period, and no extra time is needed.

5.2 Moving coordinate origin

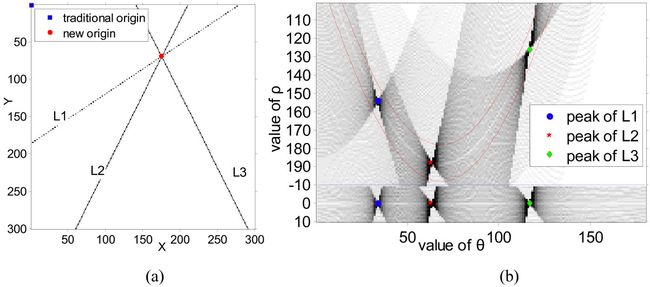
The space complexity problem of the Hough transform is due to its parameter voting mechanism (Figure  5). Figure  5a shows a synthesized edge image, including three straight line segments. The upper corner of Figure  5b shows a part of the parameter space of the Hough transform with the traditional coordinate origin setting. The lower corner of Figure  5b is part of the parameter space of the Hough transform, in which we move its coordinate origin to the intersection of these lines. Obviously, the peaks are scattered when the traditional coordinate origin is used but distributed in a straight line of  ρ = 0 under the new coordinate origin. Ideally, therefore, we only need to store the data where  ρ = 0. The improved Hough transform with a new coordinate origin uses a considerably smaller voting memory. As shown in Figure 5b, the new voting memory is marked by the two red curves in the traditional parameter space for comparison.

Figure 5

Comparison of space requirement of the Hough transform. Comparison of space requirement of the Hough transform. (a) is a synthesized edge image of three straight lines; (b) is the parameter space of the Hough transform. The upper part in (b) is the result with the traditional origin. The lower part in (b) is the result using the intersection as origin.

By analyzing (1), it is obvious that if a line goes through the coordinate origin of the Hough transform, the corresponding peak in parameter space will strictly appear in a certain line (ρ = 0). Thus, during the line detection step, the corresponding peaks will be distributed in ρ = 0 in the parameter space if the intersection (vanishing point) of these lanes is chosen as the coordinate origin of the Hough transform in every frame. The storage of the parameter space can be reduced into a 1D storage of ρ = 0 without missing any lanes.

In actual conditions, the selection of the coordinate origin in every frame cannot be restricted to the vanishing point because vehicles constantly move. Therefore, we use a range of ρ ∈ [−4σ, 4σ] to store the parameter, instead of ρ=0, where σ is determined by estimating the vanishing point position. The estimation of the vanishing point position in the next frame is analyzed in Section 6.

5.3 Vanishing point-based parallel Hough transform provides a new detection constraint

When the proposed storage strategy is implemented in the parameter space, some extra constraints are imposed on line detection. When the storage range of ρ is [−4σ, 4σ], a circle constraint of ρ = 4σ is imposed around the vanishing point. Only the lines that pass through the region of the circle are considered in the parameter space. Such a constraint eliminates numerous non-lane lines.

6 Estimation of the vanishing point position

Both the vanishing point-based steerable filter and the vanishing point-based parallel Hough transform should estimate the position of the vanishing point in the next frame. We theoretically analyzed the factors that influence the position of the vanishing point and then performed experiments to verify the distribution of the vanishing point. Finally, we considered the influence of curves on the vanishing point-based parallel Hough transform.

6.1 Factors that affect the position of the vanishing point

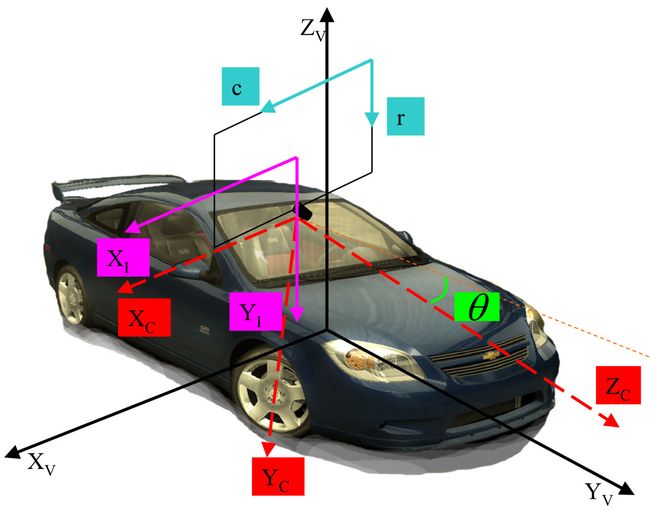
We first define some needed coordinates (Figure  6). The vanishing point in the road scene image results from the projection of any two parallel lane markings near the front of a vehicle. The two parallel lines in the vehicle coordinate appear as two intersecting lines in the camera coordinate. This intersection point is the vanishing point. The two parallel lines in the vehicle coordinate can be expressed as:

⎧⎩⎨⎪⎪⎪⎪xv_left(l)=ch0−12wRoad+ch1lxv_right(l)=ch0+12wRoad+ch1lyv(l)=lzv(l)=0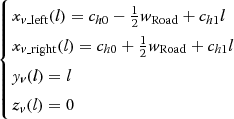

(3)

Figure 6

Coordinate. Coordinates in our system: X V Y V Z V is the vehicle coordinate, X C Y C Z C is the camera coordinate, cr is the pixel coordinate and X I Y I is the image coordinate, and θ is the pitch angle of the camera.

where c h 0 is the lateral offset of the vehicle in relation to the two parallel lane markings, and w Road is the width of the lane. c h 1 = Tan(ϕ v ) denotes the tangent of the heading angle ϕ v of the vehicle in relation to the two parallel lane markings, and l represents the arc length of the lane in the vehicle coordinate.

The onboard camera of the lane detection system is usually mounted on the vehicle carefully. The offset of the optical center in the vehicle coordinate can be assumed as (0, 0,  h), with only one non-zero parameter of the height. In the same way, the rotation angles from the vehicle coordinate to the camera coordinate are assumed to be ( p i / 2 +  θ, 0, 0), with only one non-zero parameter of pitch angle  θ. If we omit the lens distortions, the perspective projection from the 3D vehicle coordinate to the 2D frame buffer can be expressed as:

⎧⎩⎨⎪⎪c=BCI+xvcf((h−zv)sin(θ)−yvcos(θ))r=BRI+(zv−h)cos(θ)−yvsin(θ)rf((h−zv)sin(θ)−yvcos(θ))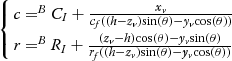

(4)

where,  cf=1Ncf 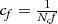 and  rf=1Nrf  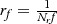represent the actual length of one pixel divided by the focus length. N c and N r are the distances between two adjacent pixels on the sensor in the horizontal and vertical directions. B C I and B R I are the coordinate values of the optical center in the frame buffer.

By substituting the description of the two parallel lane markings in the vehicle coordinate into (4) and by letting  l be infinity, we can derive the position of the vanishing point:

⎧⎩⎨⎪⎪c=BCI+tan(ϕv)cf(sin(θ)−cos(θ))r=BRI+tan(θ)rf

(5)

In actual conditions, pitch angle  θ and heading angle  ϕ  v are minimal. They are commonly maintained at less than 0.1 rad. The sinusoidal function can be expanded with the Taylor series, and all the items over the second order may be ignored. Hence, we can obtain the position of the vanishing point, thus:

⎧⎩⎨⎪⎪c=BCI+ϕvcfr=BRI+θrf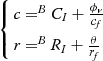

(6)

On the basis of (6), we list the factors that affect the position of the vanishing point in the road image as follows:

1. 1)

   heading angle of the vehicle ϕ v .

    
2. 2)

   pitch angle of onboard camera θ.

    
3. 3)

   actual length of one pixel divided by the focus length of onboard camera c f and r f .

    

While a vehicle is moving, the last two factors, c f and r f can be assumed constant. The variations in pitch angle θ are caused by the changes in the pitch angle of the vehicle. The heading angle is caused by the variation in vehicle maneuvers.

For simplification, we model the two factors as i.i.d. random variables with Gaussian distribution  ϕv∼N(ϕ0,σϕv)  andθ ∼ N(θ 0, σ θ ). The position of the vanishing point is a 2D random variable with Gaussian distribution,  (cvp,rvp)∼(N(BCI+ϕ0cf,σϕv),N(BRI+θ0rf,σθ)) 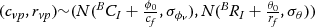, where ϕ 0 and θ 0 are the original yaw angle and pitch angle of the onboard camera relative to the vehicle. Hence, we can use the mean values of the distribution  (BCI+ϕ0cf,BRI+θ0rf) 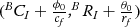, which are determined only by the extrinsic parameters of the onboard camera, as the estimated position of the vanishing point and use variance  (σϕv,σθ)  to set the search range for the actual vanishing point.

6.2 Estimation of the range of the vanishing point in experiments

To test our deductions, we have carried out experiments on the distribution of the vanishing point in actual scenes. The camera is mounted on the front of the vehicle (Figure  7). The system is set to work over 20 frames per second, and the vehicle is driven at normal speed over 50 km/h. The parameters of the vanishing point location,  θ and  ρ, in each frame are recorded. In such a case, more than 10,000 frames of data are randomly collected in different conditions, including straight and curved, ascending and descending roads, and lane changes. Figure  8 illustrates the changes in the vanishing point,  θ and  ρ when the vehicle changes from the left lane to the right. The  X-axis is the frame number, and the  Y-axis is divided into three parts. The lower part denotes the Euclidean distance of vanishing point to fixed point and their changes between adjacent frames. The middle part denotes the degree of  θ and their changes between adjacent frames. The high part denotes the distance of  ρ and their changes between adjacent frames. When the vehicle changes lanes, both of  θ and  ρ fluctuate, whereas the position of the vanishing point changes in a smooth manner. This smooth transition is the main reason why we choose the vanishing point to guide our proposed algorithms, instead of  θ or  ρ, which were used in [ 26] and in [ 5].

Figure 7

Curve case. The vanishing point-based parallel Hough transform works on curved roads. (a) and (b) are the results on the evaluation platform. (c) is the results on a highway and (d) is the results on an urban road.

Figure 8

Vanishing Point distribution. The distribution and their changes of the vanishing point, θ and ρ.

Figure  8 shows that the vanishing point changes in a smooth manner between two adjacent frames. The changes in the vanishing point position between the two adjacent frames are within a small range. The 1D Gaussian model is chosen to analyze the data changes of vanishing points between the two adjacent frames. As shown in Figure  9, the  X-axis is the distance, and the  Y-axis indicates the statistical percentage. Computing the average value  μ=1n∑nxi 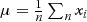and  σ2=1n∑n(xi−μ)2 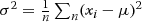, it is easy to know that 99.9% of the data are distributed between 4 σ=23 ranges.

Figure 9

Vanishing point distribution in 1D Gaussian model. The distribution of the changes between two adjacent vanishing point positions in 1D Gaussian model.

The tolerance of ρ is discussed using the estimated vanishing point, instead of the actual one, as the coordinate origin. If the distance between the estimated vanishing point and the actual one is R, then the maximum error of ρ is R.

Our analysis of the experiments yields the following recommendations. Using the estimated vanishing point to replace the coordinate origin, we set the parameter space of the Hough transform between [ ρ − R,ρ + R], instead of ρ = 0, where R is the maximum error distance between the estimated and actual vanishing points. The result of the Hough transform does not change. That is, we use the parameter space of ρ ∈ [ −4σ, 4σ], instead of the traditional ρ ∈ [−W,W], where  W=w2+h2‾‾‾‾‾‾‾√/2 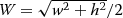, w is the width and h denotes the height of the image, the result of the Hough transform is unaffected.

In our experiments, when  w = 752,  h = 320, and 4 σ = 23, [ 817/ q  ρ ] × [  π /  q  θ ] × 10 is used in the traditional method, whereas only [ 46/ q  ρ ] × [  π /  q  θ ] × 10 is needed in the improved Hough transform.  q  ρ and  q  θ are the quantization steps of parameters  ρ and  θ, and the bit width of each bin in the parameter space is 10. The time and resources required in the traditional Hough transform are compared (Table  2), with the parallel parameter  n = 8.

Table 2

Comparison with the traditional Hough transform

Time & resource		No constraint	ρ∈ [−23, 23]
		of ρ
Parallel parameter, n=1	Time cost	100%	100%
	Resource cost	100%	5.6%
Parallel parameter, n=8	Time cost	12.5%	12.5%
	Resource cost	100%	5.6%

As shown in Table 2, we define both the time and resource requirements of the traditional Hough transform as 1 unit. Compared with the time and resources required in the traditional Hough transform, those in our improved Hough transform are 12.5% and 5.6%, respectively.

6.3 Road curves

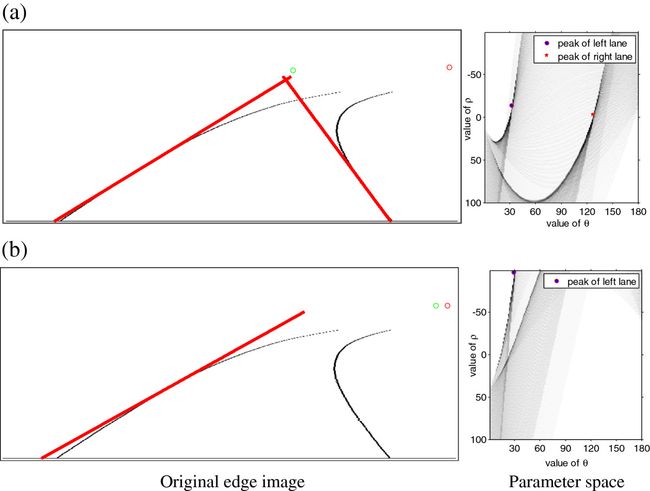
The curvature in a highway is always minimal. However, when the road direction sharply changes, as it does in sharply curved roads, the vanishing point varies. The drawback is that the Hough transform cannot accurately detect curves.

The Hough transform can detect only straight lines; hence, it identifies only the straight areas of a curved road. In such a case, the position of the vanishing point severely affects the detection results. The right side of Figure  10 is the parameter space where  ρ  ∈[−100, 100], and the left side shows the results of our improved Hough transform at different coordinate origins. The green circle in the original edge image denotes the coordinate origin, and the red one represents the actual vanishing point derived by the curves further along the scene. Two problems occur when our improved Hough transform is applied to curves. One is that the voting of pixels in lines does not accumulate at the same peak (Figure  10, upper of right side), resulting in a series of discrete peaks for the curve in the parameter space. The other problem is that the actual vanishing point is no longer suitable for the coordinate origin. When we move the coordinate origin to the actual vanishing point, the peak of the line in the parameter space easily diverges from the predefined range (Figure  10, lower of right side).

Figure 10

The drawback of VPPHT in curves. The drawback of vanishing point-based parallel Hough transform in curves. In the original images, red circle means the real vanishing point and green circle means the origin of Hough transform; red lines show the results of Hough transform. (a) shows the correct result of Hough transform when a suitable origin is used. Otherwise, the result is a mistake as shown in (b).

A number of methods that address curves have been reported [27, 28], in which the most common lane detection technique used is a deformable road model [7, 29]. Our system does not need to accurately detect lane markings in the distant part of a road. On the other hand, an accurate curve fitting algorithm is not resource-effective for embedded platforms. Thus, we use the vanishing point-based parallel Hough transform to detect the part that is approximately x m  < 30 meters as a straight line and use these results to estimate the position of the vanishing point in the next frame. That is, we do not expect the estimated vanishing point to be close to the actual one; it is predicted by the detection result for the area near the road scene.

The proposed algorithm works under different curved roads in the evaluation platform and in the on-road experiments. The results are shown in Figure 7. Although some errors occur in detecting the distant part of the curved lanes, these errors do not affect the warning results.

7 Experiments and analysis

The prototype is composed of an FPGA-based LDWS and Human-machine interface (HMI). The LDWS is fixed near the rear-view mirror (Figure  11). The HMI is mounted on the basis of driving habits. The warning signals are provided through both light and sound.

Figure 11

The proposed system. The installation of the prototype. The LDWS (upper of right side) is fixed near the rear-view mirror; the HMI (lower of right side) is placed in front of the driver. They are connected by CAN bus.

7.1 Usage of resources in our system

The system is implemented on a single FPGA chip of type xc3sd3400a-fgg676-5c. The developing environment is ISE 11.5. Very high-speed integrated circuit hardware description language (VHDL) is used in our project for unit implementation to achieve special function, while C language is used in the MicroBlaze soft core. The system clock is 40 MHz (offered by camera board), and clock frequency is doubled by DCM clock manger for some special units such as line detection unit and the MicroBlaze soft core. The time and resource usage of each unit is shown in Table 1. As previously discussed, we choose ρ ∈[−23,23] as the range of the parameter space and n = 8 in our experiment. Parallel parameter n = 8 is chosen for two reasons. One is that the θ of a lane is laid between [10∘,170∘]; thus, the improved parallel Hough transform divides the range of θ into eight pieces. In each piece, the ranges of θ are 20∘. Therefore, only one lane marking is detected as the candidate in each piece. The other reason for n=8 is that it is a compromise between time and resource usage. The time and resource usage for the proposed system is illustrated in Table 1.

The camera controller (CC) in Table 1 includes an automatic exposure control algorithm presented in [24]. The edge extraction (EE) includes the proposed vanishing point-based steerable filter. The VPPHT represents the vanishing point-based parallel Hough transform. The tracking unit and warning unit (TRW) is implemented in a MicroBlaze soft core.

The results of the experiment are compared with the system presented by Marzotto et al. [ 19], which presents a lane tracking system implemented on the same type of FPGA. Their pre-process model consists of a series of 2D filters, such as Gaussian noise reduction and Sobel convolution. In the line detection step, a lane model is chosen: a cascade of two random sample and consensus stages is applied to fit and extract lane markings. Subsequently, Kalman filtering is used to monitor the lane. Unfortunately, as a key component of the LDWS, the prototype in [ 19] does not offer a warning strategy. Some subsystems and their resources are compared in Table  3.

Table 3

Comparison with the introduced system in [ [19]]

	Module			System in [19]	This paper
	Function			Lane track	Lane track + warning
	Platform			Xilinx Spartan-3A DSP 3400	Xilinx Spartan-3A DSP 3400
	Tools			System generator for DSP (Rel. 10.1.3)	ISE 11.4
	Language			System generator scheme	VHDL
	Power (volt/watt)			Not mentioned	5V/2W
	LDWS size (millimeter)			Not mentioned	100×75 × 20
	Image size			752 × 480	752 × 320
	Frequency(frame/s)			30	40
	Line detection method			Model fitting	Proposed Hough transform
	External memory used			Not mentioned	No
	Tracking unit			Special designed by HDL	Working in MicroBlaze
Resource		Preprocess	DSP48	12 (9%)	5 (4%)
			BRAM	16 (12%)	6 (5%)
			Slices	2,594 (10%)	2,601 (10%)
		Line detection	DSP48	17 (13.5%)	16 (12.7%)
			BRAM	14 (11.1%)	40 (31.7%)
			Slices	3,120 (13.1%)	1,091 (4%)
		T&W	DSP48	5 (4%)	4 (3%)
			BRAM	2 (1.6%)	64 (50.8%)
			Slices	2,686 (11.2%)	2,144 (9%)
		DCM clock manager		Not mentioned	3

The comparison shows that most of the parts in our system consume fewer resources than those in [19]. In the line detection unit, our improved Hough transform uses part of BRAM as parameter storage. In the lane tracking unit, although the MicroBlaze soft core uses considerable resources, it can accommodate future developments. In other words, the tracking function in [19] is fixed; improvements or the addition of new functions are difficult to accomplish. By contrast, the functions of MicroBlaze in our system are easy to change, improve, and have new functions added.

7.2 Evaluation experiments

An emulation platform was specially designed to test the performance of our algorithm. The platform was expanded from the programs presented by Lopez [30]. The evaluation platform generates sequences of synthetic but realistic images from exactly known road geometry and camera parameters. With both the intrinsic and extrinsic parameters of the camera, the platform determines the relationship between a vehicle and a road in each frame.

We define the standard warning time in our platform as follows.

The standard time spent crossing a lane (ground truth) pertains to the time that begins at the ego frame to the frame in which the vehicle actually crosses the lane. The parameter is generated by the platform.

t={tc−te10tc−te<10tc−te≥10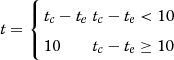

(7)

In its equation, t c is the time spent by a vehicle as it crosses a lane in the future, and t e denotes the ego time.

The standard warning time spent crossing the left (right) lane (ground truth) pertains to keeping the direction and velocity unchanged and the time between the ego position to that at which a vehicle crosses the left (right) lane. The parameter is generated by the platform. Its equation is t = d / v, where d is the distance between the ego position and the point where the vehicle crosses the left (right) lane in the future; v denotes the current velocity.

The user’s warning time for crossing the left (right) lane is generated by the user’s warning algorithm.

For the false alarm, N i  = 1 when the user’s algorithm triggers the alarm but not in the ground truth in the i th frame; otherwise, N i  = 0.

For the failed alarm, F i  = 1 when the user’s algorithm does not trigger the alarm but should do in the ground truth in the i th frame; otherwise, F i  = 0.

The efficiency of the user’s warning strategy:  E=1−∑n1Ni+∑n1Fin .

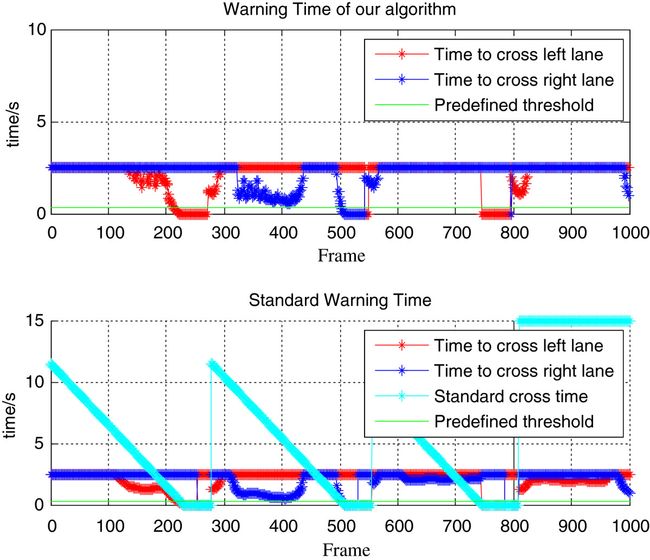
The proposed algorithm was tested on this evaluation platform, which randomly generated thousands of sequence scenes. Straight roads and curves indicated that the vehicle repeatedly changes lanes. The results are shown in Figure 12. In relation to the ground truth, the efficiency levels of our warning strategy are  E  left = 93.65 %,  E  right = 95.54 %.

Figure 12

The evaluation of warning system. The results of our evaluation. Upper part is the result of our algorithm; lower part is the ground truth.

7.3 Results of experiments on actual roads

To test the system and its algorithms, we conducted numerous on-road experiments on a prototype device (Figure 11).

The prototype works in different kinds of environments. The performance levels on urban roads, as well as under the presence of weak markings or disruptions by other vehicles are shown in Figure  13. Some challenging road conditions, such as wet weather, nighttime, and driving through a tunnel, are also depicted in Figure  13. The small cross in Figure  13denotes the position of the vanishing point, and the circle around the vanishing point represents the parameter space range of  ρ = 4 σ, which is also the lane constraint, in which only the lines that go through the circle are detected. The warning time is tagged beside the marked lane; if it exceeds the previously established threshold, the alarm will be triggered.

Figure 13

Actual road experiments. Results in various scenarios. (a) Urban road and vehicle disturbing. (b) Worn off marks. (c) Rainy. (d)Night. (e) Exit of a tunnel. In the left parts are the original images. The small cross in the right parts denotes the position of the vanishing point, and the circle around the vanishing point represents the parameter space range of ρ = 4σ. Red line means the tracked lane marking, and warning time is tagged beside the marked lane. Yellow line means the alarm is triggered.

On-road testing was implemented both in an urban environment and on highways in Hunan province, China. Figure  14shows the map of Changsha City. To complete our test, we chose an approximately 40-km highway and 16-km urban roads, denoted in green color in the figure.

Figure 14

The map of actual road experiments. Route of our experiments in Hunan Province. (a) is a highway around Changsha City (40 km); (b) is an urban road in Changsha City (16 km).

Testing on actual roads is dangerous for drivers because they are compelled to cross or change lanes without using turning signals, as required to determine whether the system works. Moreover, on-road testing is a difficult task, for whether it should give a warning is hard to tell, especially when the vehicle is driving along one side of the lane [31]. To the best of our knowledge, no method to test an LDWS is available in on-road experiments for both the rate of failed alarms and the rate of false alarms. Here, ‘failed alarm’ means that the system does not issue a warning when it should, and ‘false alarm’ indicates that the system issues a warning when it is not supposed to. Therefore, the warning rate defined in our evaluation platform is impossible to implement in testing on an actual road. We designed our actual road tests as Barickman et al. [31] did: a driver randomly crosses or changes lanes, then registers whether the system correctly triggers the alarm. This way, the failed alarm rate of the system could be estimated. Hundreds of tests on highways have yielded the following results: the accuracy of the warning rate of our system is approximately 99% under cloudy or sunny conditions, approximately 97% in rainy or foggy conditions, and approximately 95% at nighttime.

Our system is presumed to be almost 100% accurate on the highway under good weather. It also performs well in rainy or foggy conditions. At night, the system may sometimes be disrupted by strong light from on-coming vehicles. We did not conduct an urban road experiment because it was too dangerous to carry out considering the number of vehicles on the road. With regular lane markings but no other vehicles around to disrupt the system, testing on urban roads is meaningless because the environment would be almost the same as that on a highway. Although our system provides no list with data on an urban environment, some results are offered in the attachments to describe the results on an urban road (Figure 13a).

The results are compared with those of state-of-the-art prototypes. Hsiao et al. proposed an FPGA + ARM-based LDWS [23]. First, a line detection algorithm based on ‘the peak finding for feature extraction’ is used to detect lane boundaries. Subsequently, a spatiotemporal mechanism that uses detected lane boundaries is designed to generate appropriate warning signals. Hsiao et al. [32] presents an LDWS on an embedded microprocessor with a Windows CE 5.0 platform. Unfortunately, the warning rate in [32] is given superficially. Neither experiment details nor ways of getting the warning rate are introduced in this paper.

The results of the comparison are shown in Table  4. Our system is suitable for more types of weather conditions (sunny, cloudy, rain, fog) and environments (highways and urban roads) and exhibits a higher computational efficiency (it can handle large images and execute faster processing).

Table 4

Comparing with other LDWSs

	Our system	Paper [23]	Paper [32]
Image size	752 × 320	256 × 256	320 × 240
Road environment	Highway and urban	Highway	Not mentioned
Weather	Sunny, rainy, fog, cloudy	Not mentioned	Not mentioned
Platform	FPGA	FPGA+ARM	Microprocessor
External storage	No	16M SDARM	1G system memory
Frequency(frame/s)	40	25	15
Warning rate	99% during the day	92.45% during the day	97.9% during the
	95% at night, 97% in rainy	91.83% at night	Day and night

8 Conclusions

We present an LDWS based on FPGA technology. The system has two main components: specialized vision processing engines and an embedded MicroBlaze soft core, which corresponded to SIMD and SISD computing structures. Using the estimated vanishing point, we improved the traditional steerable filter and implemented it on the FPGA device in parallel. An improved vanishing point-based parallel Hough transform based on the SIMD structure is also proposed. By moving the coordinate origin to the estimated vanishing point, we reduce the storage requirement of the proposed Hough transform to approximately 5.6%. The position of the vanishing point is then theoretically and experimentally analyzed. The effect of curves is also considered. To test the efficiency of our system, we designed an evaluation platform.

A prototype based on xc3sd3400a-fgg676-5c is implemented, and the results of on-road experiments are provided. Some tests under challenging conditions show that our method enables good performance and that the system is reliable. Tests on a highway and on urban roads were implemented in Hunan Province. The system worked well, except when there were no lane markings.

More details of experiment results are offered by the videos in Additional file 1. Video 1 shows the result of the evaluation experiment. Videos 2 and 3 are offered to describe the results on an urban road. The performance levels on urban roads as well as under the presence of weak markings or disruptions by other vehicles are shown in videos 4 and 5. Some challenging road conditions, such as wet weather (video 6), nighttime (video 7), and driving through a tunnel (video 8) are also depicted; video 9 shows the result of highway.

Sometimes, when a vehicle moves very slowly, the driver may be weaving down the road and thus sharply change the heading angle of the vehicle. In such a case, the range of the heading angle considerably increases, and the range of the vanishing point position exceeds the previously established value. On the other hand, when the pathway on an urban road is too curved, our system continues to function, but the warning system becomes too sensitive because of the straight-line Hough transform algorithm. A velocity limitation is incorporated into the warning system to avoid these problems. The warning system functions only when a vehicle is driven over a speed of 30 km/h. In some cases, the system loses the vanishing point position during tracking when no line markings are on the road. In such circumstances, the position of the vanishing point is automatically re-estimated from a previously established point.

Declarations

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China: 90820302.

Electronic supplementary material

13640_2012_76_MOESM1_ESM.zip  Additional file 1: Videos about experiment results. Attachments are some videos about experiment results of this paper: The prototype works in different kinds of environments. Video 1 shows the result of evaluation experiment; videos 2 and 3 are offered to describe the results on an urban road. The performance levels on urban roads, as well as under the presence of weak markings or disruptions by other vehicles are shown in videos 4 and 5. Some challenging road conditions, such as wet weather (video 6), nighttime (video 7), and driving through a tunnel (video 8) are also depicted; video 9 shows the result of highway. (ZIP 113 MB)

Authors’ original submitted files for images

Below are the links to the authors’ original submitted files for images.

13640_2012_76_MOESM2_ESM.pdf  Authors’ original file for figure 1

13640_2012_76_MOESM3_ESM.pdf  Authors’ original file for figure 2

13640_2012_76_MOESM4_ESM.pdf  Authors’ original file for figure 3

13640_2012_76_MOESM5_ESM.pdf  Authors’ original file for figure 4

13640_2012_76_MOESM6_ESM.pdf  Authors’ original file for figure 5

13640_2012_76_MOESM7_ESM.pdf  Authors’ original file for figure 6

13640_2012_76_MOESM8_ESM.pdf  Authors’ original file for figure 7

13640_2012_76_MOESM9_ESM.pdf  Authors’ original file for figure 8

13640_2012_76_MOESM10_ESM.pdf  Authors’ original file for figure 9

13640_2012_76_MOESM11_ESM.pdf  Authors’ original file for figure 10

13640_2012_76_MOESM12_ESM.pdf  Authors’ original file for figure 11

13640_2012_76_MOESM13_ESM.pdf  Authors’ original file for figure 12

13640_2012_76_MOESM14_ESM.pdf  Authors’ original file for figure 13

13640_2012_76_MOESM15_ESM.pdf  Authors’ original file for figure 14

Competing interests

The authors declare that they have no competing interests.

Authors’ Affiliations

(1)

College of Mechatronic Engineering and Automation, National University of Defense Technology

References

1. McCall J, Trivedi M: Video-based lane estimation and tracking for driver assistance: survey, system, and evaluation. Intell. Trans. Syst., IEEE Trans 2006, 7: 20-37. 10.1109/TITS.2006.869595View Article
2. Veit T, Tarel J, Nicolle P, Charbonnier P: Evaluation of road marking feature extraction. In 11th International IEEE Conference on Intelligent Transportation Systems. Beijing; 12–15 Oct 2008:174-181.
3. Deriche R: Using Canny’s criteria to derive a recursively implemented optimal edge detector. Int. J. Com. Vis 1987, 1(2):167-187. 10.1007/BF00123164View Article
4. McCall J, Trivedi M: An integrated, robust approach to lane marking detection and lane tracking. In Intelligent Vehicles Symposium. Parma; 14–17 Jun 2004:533-537.
5. Guo L, Li K, Wang J, Lian X: Lane detection method by using steerable filters. Jixie Gongcheng Xuebao (Chinese J. Mech. Eng.)2008, 44(8):214-218. 10.3901/JME.2008.08.214View Article
6. Anvari R: FPGA Implementation of the lane detection and tracking algorithm. PhD thesis, The University of Western Australia Faculty of Engineering, Computing and Mathematics School of Electrical, Electronic and Computer Engineering Centre for Intelligent Information Processing Systems (2010)
7. Yu B, Zhang W, Cai Y: A lane departure warning system based on machine vision. In Pacific-Asia Workshop on Computational Intelligence and Industrial Application. Wuhan; 19–20 Dec 2008:197-201.
8. Chen Q, Wang H: A real-time lane detection algorithm based on a hyperbola-pair model. In Intelligent Vehicles Symposium. Tokyo; 13–15 Jun 2006:510-515.View Article
9. Foucher P, Sebsadji Y, Tarel J, Charbonnier P, Nicolle P: Detection and recognition of urban road markings using images. In 14th International IEEE Conference on Intelligent Transportation Systems (ITSC). Washington, DC; 5–7 Oct 2011:1747-1752.
10. Zhou S, Jiang Y, Xi J, Gong J, Xiong G, Chen H: A novel lane detection based on geometrical model and Gabor filter. In Intelligent Vehicles Symposium (IV),. San Diego; 21–24 Jun 2010:59-64.
11. Linarth A, Angelopoulou E: On feature templates for particle filter based lane detection. In 14th International IEEE Conference on Intelligent Transportation Systems (ITSC). Washington, DC; 5–7 Oct 2011:1721-1726.
12. Kim B, Son J, Sohn K: Illumination invariant road detection based on learning method. In 14th International IEEE Conference on Intelligent Transportation Systems (ITSC). Washington, DC; 5–7 Oct 2011:1009-1014.
13. Kim D, Jin S, Thuy N, Kim K, Jeon J: A real-time finite line detection system based on FPGA. In 6th IEEE International Conference on Industrial Informatics. Daejeon; 13–16 Jul 2008:655-660.
14. El Mejdani S, Egli R, Dubeau F: Old and new straight-line detectors: description and comparison. Pattern Recognit 2008, 41(6):1845-1866. 10.1016/j.patcog.2007.11.013View Article
15. Li Q, Zheng N, Cheng H: Springrobot: A prototype autonomous vehicle and its algorithms for lane detection. Intell. Trans. Syst., IEEE Trans 2004, 5(4):300-308. 10.1109/TITS.2004.838220View Article
16. Fardi B, Wanielik G: Hough transformation based approach for road border detection in infrared images. In Intelligent Vehicles Symposium. Parma; 14–17 Jun 2004:549-554.
17. Fernandes L, Oliveira M: Real-time line detection through an improved Hough transform voting scheme. Pattern Recognit 2008, 41: 299-314. 10.1016/j.patcog.2007.04.003View Article
18. Chern M, Lu Y: Design and Integration of Parallel Hough-Transform Chips for High-speed Line Detection. In Proceedingsof the 11th International Conference on Parallel and Distributed Systems. Fukuoka; 22 Jul 2005:42-46.
19. Marzotto R, Zoratti P, Bagni D, Colombari A, Murino V: A real-time versatile roadway path extraction and tracking on an FPGA platform. Comput. Vis. Image Underst 2010, 114(11):1164-1179. 10.1016/j.cviu.2010.03.015View Article
20. McDonald J: Application of the hough transform to lane detection and following on high speed roads. In Proceeding of Irish Signals and Systems Conference in Motorway Driving Scenarios. Maynooth; 25–27 June 2001.
21. Stein G, Rushinek E, Hayun G, Shashua A: A Computer Vision System on a Chip: a case study from the automotive domain. InProceedings of the International IEEE Conference on Computer vision and Pattern recognition. San Diego; 25 Jun 2005:130-134.
22. Vitabile S, Bono S, Sorbello F: An embedded real-time lane-keeper for automatic vehicle driving. In International Conference on Complex, Intelligent and Software Intensive Systems. Barcelona; 4–7 Mar 2008:279-285.View Article
23. Hsiao P, Yeh C, Huang S, Fu L: A portable vision-based real-time lane departure warning system: day and night. Vehicular Technol., IEEE Trans 2009, 58(4):2089-2094.View Article
24. Pan S, An X: Content-based auto exposure control for on-board CMOS camera. In 11th International IEEE Conference on Intelligent Transportation Systems. Beijing; 12–15 Oct 2008:772-777.
25. Freeman W, Adelson E: The design and use of steerable filters. IEEE Trans. Pattern Anal. Mach. Intell 1991, 891-906.
26. Kuk J, An J, Ki H, Cho N: Fast lane detection & tracking based on Hough transform with reduced memory requirement. In 13th International IEEE Conference on Intelligent Transportation Systems (ITSC). Funchal; 19–22 Sept 2010:1344-1349.View Article
27. Zhao S, Farrell J: Optimization-based Road Curve Fitting. In Decision and Control and European Control Conference (CDC-ECC) 2011 IEEE Conference on. : IEEE; 2011:5293-5298.
28. Apostoloff N, Zelinsky A: Robust vision based lane tracking using multiple cues and particle filtering. In Intelligent Vehicles Symposium. Colombus; 9–11 Jun 2003:558-563.
29. Wang H, Chen Q: Real-time lane detection in various conditions and night cases. In Intelligent Transportation Systems Conference. Toronto; 17-20 Sept 2006:1226-1231.
30. López A, Serrat J, Cañero C, Lumbreras F, Graf T: Robust lane markings detection and road geometry computation. Int. J. Automot. Technol 2010, 11(3):395-407. 10.1007/s12239-010-0049-6View Article
31. Barickman F, Jones R, Smith L: Lane departure warning system research and test development. In Proceedings of the 20th International Conference on the Enhanced Safety of Vehicles. Lyon; 18–21 Jun 2007:1-8.
32. Hsiao P, Hung K, Huang S, Kao W, Hsu C, Yu Y: An embedded lane departure warning system. In IEEE 15th International Symposium on Consumer Electronics (ISCE). Singapore; 14–17 Jun 2011:162-165.View Article

Copyright

© An et al.; licensee Springer. 2013

This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://​creativecommons.​org/​licenses/​by/​2.​0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.