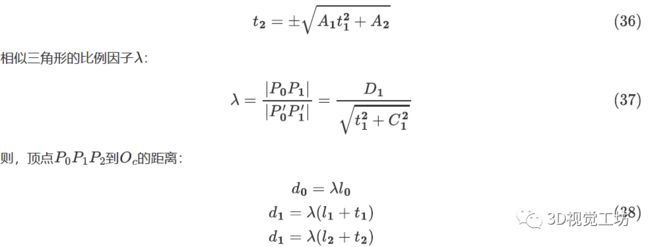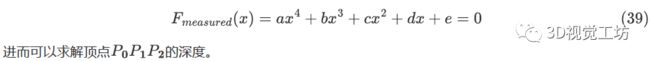一文详解PnP算法原理

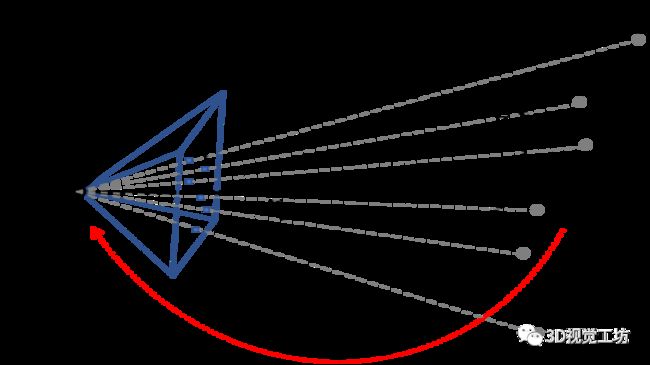
PnP(Perspective-n-Point)问题的几何结构如图1所示，给定3D点的坐标、对应2D点坐标以及内参矩阵，求解相机的位姿。

数学语言描述如下：

图1.PnP几何结构

1.直接线性变换法(Direct Linear Transform，DLT)

假设：摄像机已经校准过了。

已知：

求解相机的外参：R、t

透视投影模型为：

每组3D-2D匹配点对应两个方程，一共有12个未知数，至少需要6组匹配点。

设有N组匹配点，则：

上式写成矩阵形式：

AF=0

当N=6时，可以直接求解线性方程组。

因此, 旋转矩阵, 平移矩阵求得:

2.P3P

P3P问题是已知三个3D目标点与其2D投影之间的对应关系，来确定标定相机的位姿问题。

图2.两点约束

注：直接线性变换法，只考虑了线性意义下的最优解，没有考虑几何约束。而P3P考虑了三角约束，给出三角约束意义下的最优解

2.1 Zero Structure for the P3P Equation System

文章[1]：Complete Solution Classification for the Perspective-Three-Point Problem

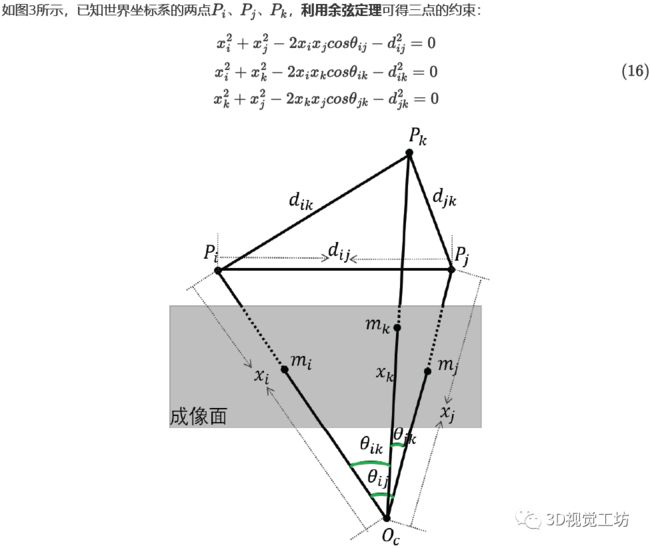
图3.三点约束

对于公式（16）的变量有一些真实的约束：

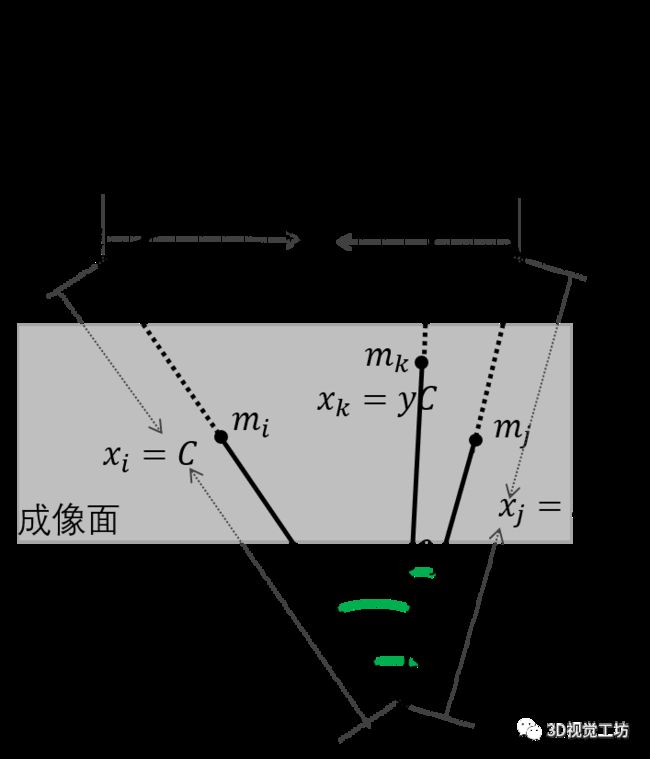
图4.三点约束--重定义边长

公式(17)消去C、v，得ES：

2.2 PST

文章[2]：A Stable Direct Solution of Perspective-Three-Point Problem

使用相似三角形，利用几何约束来减少未知参数的个数，把P3P方程组转化为四次方程，该称为透视相似三角形方法(Perspective Similar Triangle ，PST)。

（1）P3P问题转为PST问题

图5.P3P几何结构

（2）PST的求解

图6.PST几何结构

约束1：相似三角形对应边成比例

所以：

（3）PST多解和缺解问题

由PST(perspective similar Triangle)求解，可得方程组等效转换为四次多项式

多解问题：

由于存在多组解，相机位姿不能从3点集唯一确定的。解的个数直接对应于四次多项式实根的个数。要得到唯一的解，至少还应引入一点，构建2个三角形，进行求解。另一种方法是RANSAC算法，该算法将点集划分为3个点子集，检查这些子集的一致性。

RANSAC算法参考文献：Random Sample  Consensus: A  Paradigm for Model  Fitting with  Apphcatlons to Image  Analysis and  Automated  Cartography

缺解问题：

缺解问题是由P3P的固有结构决定的，其他P3P方法，如迭代解法、几何解法和分类法，也有同样的问题。

3.RPnP

文章[3]：A Robust O(n) Solution to the Perspective-n-Point Problem

下面来看一下，如何建立新的正交坐标系，以及如何求解正交坐标系到相机坐标系之间[R T]。

3.1确定旋转轴

当确定旋转轴时，只需求解剩余的旋转和三个平移参数，减少了未知变量的数量，来提高方程组的数值精度。

3.2求解旋转角和平移矢量的方程

相机坐标系与新坐标系绕之间的旋转矩阵：

其中,

3.3获取相机的位姿

再获取到相机坐标系与新坐标系绕之间的旋转和平移矩阵，进而可直接相机坐标系与世界坐标系绕之间旋转和平移矩阵，即相机的位姿。

引文：

[1] Gao, X. S. , et al. "Complete solution classification for the perspective-three-point problem." IEEE Transactions on Pattern Analysis & Machine Intelligence 25.8(2003):930-943.

[2] Li, S. , and  X. Chi . "A Stable Direct Solution of Perspective-Three-Point Problem." International Journal of Pattern Recognition and Artificial Intelligence 25.5(2011):627-642.

[3] Li, S. ,  X. Chi , and  X. Ming . "A Robust O(n) Solution to the Perspective-n-Point Problem." IEEE Transactions on Pattern Analysis and Machine Intelligence (2012).

[4]W. Press, S. Teukolsky, W. Vetterling, and B. Flannery,Numerical Recipes:The Art of Scientific Computing.Cambridge Univ. Press, 2007.

[5]S. Umeyama, “Least-Squares Estimation of Transformation Parameters between Two Point Patterns,”IEEE Trans. Pattern Analysis and Machine Intelligence,vol. 13, no. 4, pp. 376-380, Apr. 1991.

备注：作者也是我们「3D视觉从入门到精通」知识特邀嘉宾：一个超干货的3D视觉学习社区

原创征稿

初衷
3D视觉工坊是基于优质原创文章的自媒体平台，创始人和合伙人致力于发布3D视觉领域最干货的文章，然而少数人的力量毕竟有限，知识盲区和领域漏洞依然存在。为了能够更好地展示领域知识，现向全体粉丝以及阅读者征稿，如果您的文章是3D视觉、CV&深度学习、SLAM、三维重建、点云后处理、自动驾驶、三维测量、VR/AR、3D人脸识别、医疗影像、缺陷检测、行人重识别、目标跟踪、视觉产品落地、硬件选型、求职分享等方向，欢迎砸稿过来~文章内容可以为paper reading、资源总结、项目实战总结等形式，公众号将会对每一个投稿者提供相应的稿费，我们支持知识有价！

投稿方式

邮箱：[email protected] 或者加下方的小助理微信，另请注明原创投稿。

▲长按加微信联系

▲长按关注公众号