4.基于深度学习的轴承故障诊断--SVD去噪

该专栏将较为详细的介绍如何利用深度学习进行故障诊断方面的学术研究，主要以轴承为例，包括深度学习常用框架Tensorflow的搭建以及使用，并会记录完整搭建过程，并以卷积神经网络与循环神经网络为例进行代码编写和实际运行，相信经过本次学习，你能够入门开始着手研究。

完成该专栏的学习，你将会收获以下知识：

1.Anaconda的安装以及使用，深度学习框架Tensorflow2的安装以及使用

2.学会如何利用卷积神经网络与循环神经网络进行轴承故障诊断-以凯斯西楚大学轴承数据集为例

3.学会一些常用调参技巧

4.入门利用深度学习进行故障诊断的学术研究

说明：

1.专栏所涉及代码会全部公开在本人的github上，欢迎交流以及star。

https://github.com/boating-in-autumn-rain?tab=repositories
2.该专栏涉及数据集以及相关安装包在公众号《秋雨行舟》回复轴承即可领取。

3.该专栏对应的视频可在B站搜索《秋雨行舟》进行观看学习。

SVD去噪代码：

# 博客：https://blog.csdn.net/qq_38918049/article/details/124948664?spm=1001.2014.3001.5501
# github：https://github.com/boating-in-autumn-rain?tab=repositories
# 微信公众号：秋雨行舟
# B站：秋雨行舟
#
# 该项目涉及数据集以及相关安装包在公众号《秋雨行舟》回复轴承即可领取。
# 对于该项目有疑问的可以在上述四个平台中留言，看到了就会回复。
# 该项目对应的视频可在B站搜索《秋雨行舟》进行观看学习。
# 欢迎交流学习，共同进步

from sign import preprocess
from scipy.linalg import hankel
import numpy as np
import random
import matplotlib.pyplot as plt

def new_data():
    length = 1024
    number = 200  # 每类样本的数量
    normal = True  # 是否标准化
    rate = [0.5, 0.25, 0.25]  # 测试集验证集划分比例

    path = r'data/0HP'
    Train_X, Train_Y, Valid_X, Valid_Y, Test_X, Test_Y = preprocess.prepro(
    d_path=path,
    length=length,
    number=number,
    normal=normal,
    rate=rate,
    enc=False, enc_step=28)


    x_train = np.array(Train_X)
    y_train = np.array(Train_Y)
    x_test = np.array(Test_X)
    y_test = np.array(Test_Y)
    y_test = np.squeeze(y_test)

    return  x_train, y_train, x_test, y_test

x_train, y_train, x_test, y_test = new_data()

# 噪声公式
def wgn(x, snr):
    snr = 10 ** (snr / 10.0)
    xpower = np.sum(x ** 2) / 1024
    npower = xpower / snr
    random.seed(1)
    noise1 = np.random.randn(1024) * np.sqrt(npower)
    return x + noise1

t = np.arange(0, 1024, 1)
fig2 = plt.figure().add_subplot(111)
fig2.plot(t, list(x_train[500]), 'b', label='Original data')
fig2.legend()
fig2.set_xlabel('Sampling point', size=15)
fig2.set_ylabel('Value of data', size=15)
plt.show()


# 向某一条训练样本添加噪声

x_train[500] = wgn(x_train[500], 0)


## 1.待处理信号(1024个采样点)
t = np.arange(0, 1024, 1)

## 2.一维数组转换为二维矩阵
x2array = hankel(x_train[500][0:512], x_train[500][512:1024])

## 3.奇异值分解
U, S, V = np.linalg.svd(x2array)
S_list = list(S)

## 奇异值求和
S_sum = sum(S)

##奇异值序列归一化
S_normalization_list = [x for x in S_list]

E = 0
for i in range(len(S_list)):
    E = S_list[i] * S_list[i] + E

p = []
for i in range(0, len(S_list)):
    if i == len(S_list)-1:
        p.append((S_list[i] * S_list[i]) / E)
    else:
        p.append(((S_list[i] * S_list[i]) - (S_list[i+1] * S_list[i+1])) / E)

X = []
for i in range(len(S_list)):
    X.append(i + 1)

fig1 = plt.figure().add_subplot(111)
fig1.plot(X, p)
fig1.set_xlabel('jieci', size=15)
fig1.set_ylabel('nengliangchafennpu', size=15)
plt.show()

# 4.画图
X = []
for i in range(len(S_list)):
    X.append(i + 1)

fig1 = plt.figure().add_subplot(111)
fig1.plot(X, S_normalization_list)
fig1.set_xlabel('Rank', size=15)
fig1.set_ylabel('Normalize singular values', size=15)
plt.show()

## 5.数据重构
K = 20  ## 保留的奇异值阶数
for i in range(len(S_list) - K):
    S_list[i + K] = 0.0

S_new = np.mat(np.diag(S_list))
reduceNoiseMat = np.array(U * S_new * V)

reduceNoiseList = []
for i in range(512):
    reduceNoiseList.append(reduceNoiseMat[i][0])

for i in range(512):
    reduceNoiseList.append((reduceNoiseMat[len(x2array)-1][i]))

## 6.去燥效果展示
fig2 = plt.figure().add_subplot(111)
fig2.plot(t, list(x_train[500]), 'b', label='Original data')
fig2.plot(t, reduceNoiseList, 'r-', label='Processed data')
fig2.legend()
fig2.set_title('Rank is 1')
fig2.set_xlabel('Sampling point', size=15)
fig2.set_ylabel('Value of data', size=15)
plt.show()

为什么利用SVD能够达到去噪，即SVD去噪原理可在B站搜索《秋雨行舟》看视频讲解，详细数学公式推导还请自行百度，下面是运行截图。

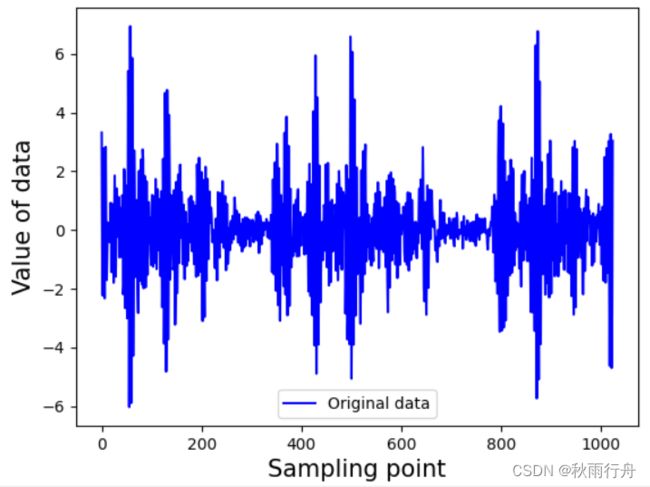
原始振动信号展示：

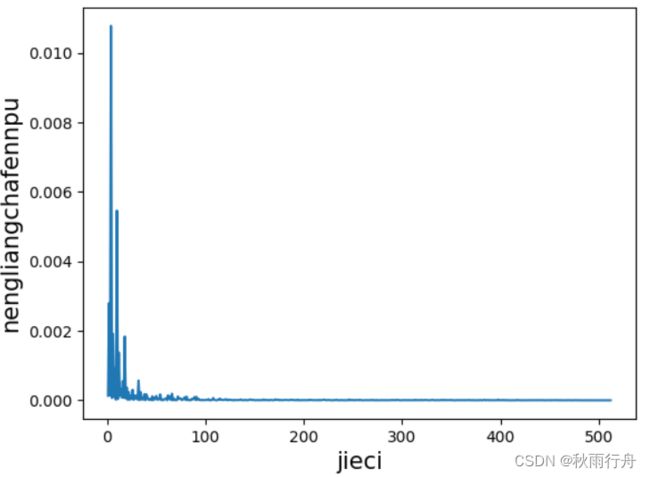
 能量差分谱展示：能量差分谱的数学公式可在中国知网搜索相关文献查看。

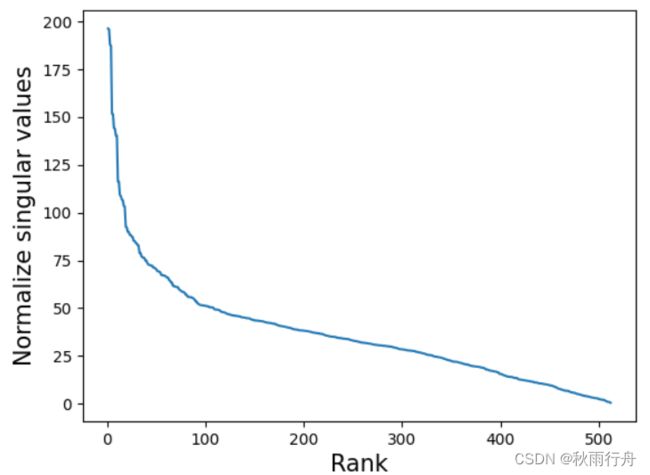
 不同阶次对应的值：

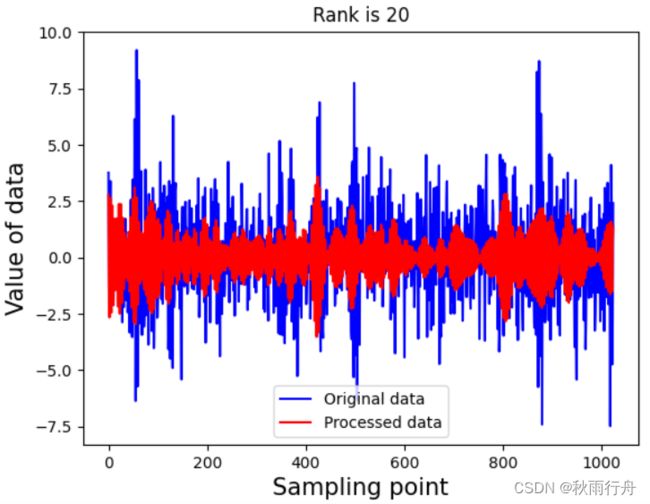
0db信噪比的含噪信号与去噪信号展示：

最后，如有疑问，欢迎交流，共同进步。