【数字图像处理】实验三 图像分割（MATLAB实现）

目录

一、实验意义及目的

二、实验内容

三、Matlab 相关函数介绍

四、算法原理

五、参考代码及扩展代码流程图

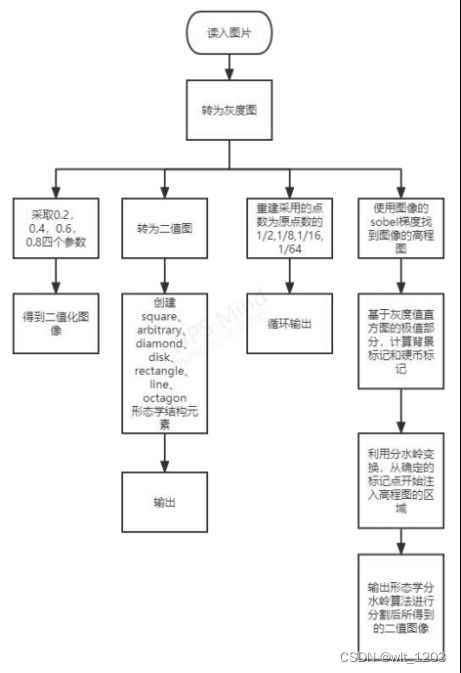
(1)参考代码流程图

(2)扩展代码流程图

六、参考代码

七、实验要求

（1）尝试不同的阈值选择方法，实现灰度图像二值化

（2）变换参数实现形态学滤波，查看滤波效果

（3）更改重建边界点数，查看效果

（4）自行设计方法实现图像分割，并计算分割区域相关参数

---

一、实验意义及目的

（ 1 ）进一步掌握图像处理工具 Matlab ，熟悉基于 Matlab 的图像处理函数。

（2）掌握图像分割方法，熟悉常用图像描述方法。

二、实验内容

打开一幅图像 Image ，使用 Matlab 图像处理函数，对其进行下列变换：

（ 1 ）将 Image 灰度化为 gray ，对其进行阈值分割转换为 BW ；

（2）对 BW 进行数学形态学滤波；

（3）对 BW 进行边缘跟踪，用红色线在图中标出；

（4）计算各区域边界点的傅里叶描绘子并用四分之一点重建边界；

（5）实验要求中的拓展内容。

三、Matlab 相关函数介绍

（1）im2bw 函数

BW = im2bw(I, level) ：以 level 为阈值把灰度图像 I 转变为二值图像。

（2）graythresh 函数

level = graythresh(I) ，使用 Otsu 方法获取阈值， level 被归一化到 [0,1] 区间。

（3）imbinarize 函数

BW = imbinarize(I) ：采用基于 OTSU 方法的全局阈值实现灰度图像 I 的二值化。

BW = imbinarize(I, METHOD) ：采用 METHOD 指定的方法获取阈值实现灰度图像 I 的

二值化。 METHOD 可选 'global' 和 'adaptive' ，前者指定 OTSU 方法，后者采用局部自适应阈值

方法。

（4）bwboundaries 函数

搜索二值图像 BW 的外边界和内边界。

[B,L,N,A] = bwboundaries(BW,CONN,OPTIONS) ：函数视 BW 中为 0 的元素为背景像素

点，为 1 的元素为待提取边界目标。 B 中的每个元素均为 Q×2 矩阵，矩阵中每一行包含边界

像素点的行坐标和列坐标， Q 为边界所含像素点的个数。 L ，标识矩阵，标识二值图像中被边

界所划分的区域； N ，区域的数目 N ； A ，被划分的区域的邻接关系。 CONN 取 4 ，搜索中采

用 4 连通方法，默认取 8 ，即 8 连通方法。 OPTIONS 指定算法的搜索方式，默认为 ‘holes’ ，

搜索目标的内外边界， ‘noholes’ 只搜索目标的外边界。

（5）bwtraceboundary 函数跟踪二值图像 BW 中目标轮廓。

B = bwtraceboundary(BW,P,FSTEP) ：目标区域取值非 0 ；参数 P 是初始跟踪点的行列坐标

二元矢量； FSTEP 表示初始查找方向，用于寻找对象中与 P 相连的下一个像素，可取 'N' 、 'NE' 、

'E' 、 'SE' 、 'S' 、 'SW' 、 'W' 、 'NW' ；返回值 B 为边界坐标值，是一个 Q×2 矩阵。

（6）strel 函数

  创建形态学结构元素。

  SE = strel(shape,parameters) ，创建一个由 shape 指定的结构元素，其中 shape 的种类有：

  arbitrary 、 pair 、 diamond 、 periodicline 、 disk 、 rectangle 、 line 、 square 、 octagon ，参数     parameters

  一般控制 SE 的大小。

（7）imdilate 函数

  IM2 = imdilate(IM, SE) ：膨胀图像 IM ，返回膨胀后的图像 IM2 ， SE 是结构元素。

（8）imerode 函数

  IM2 = imerode(IM,SE) ：腐蚀图像 IM ，返回腐蚀后的图像 IM2 ， SE 是结构元素。

（9）imopen 函数

  IM2 = imopen(IM,SE) ：对图像 IM 进行开运算，返回图像为 IM2 ， SE 是结构元素。

（10）imclose 函数

  IM2 = imclose(IM,SE) ：对图像 IM 进行闭运算，返回图像为 IM2 ， SE 是结构元素。

（11）fft 和 fft2 函数

  fft(X) ：对序列 X 进行 DFT 运算。

  fft2(X) ：对矩阵 X 进行二维 DFT 运算。

（12）ifft 和 ifft2 函数

  ifft(X) ：对 X 进行 IDFT 运算。

  ifft2(F)：对 F 进行二维 IDFT 运算。

四、算法原理

  图像分割是指把一副图像分成不同的具有特定性质区域的图像处理技术，将这些区域提取出来以便进一步提取特征，是由图像处理到图像分析的关键步骤。图像分割由于其重要性一直是图像处领域的研究重点。其中阈值分割方法是根据图像灰度值的分布特性确定某个阈值来进行图像分割的一种方法。设原灰度图像为 f (x, y) ，通过某种准则选择一个灰度值T 作为阈值，比较各像素值与T 的大小关系：像素值大于等于T 的像素为一类，变更像素值为 1；像素值小于T 的像素点为另一类，变更其像素值为 0。公式如下：

    

 

而边界跟踪是指根据某些严格的“探测准则”找出目标物体轮廓上的像素，即确定边界的起 始搜索点。在根据一定的“跟踪准则”找出目标物体上的其他像素，直到符合跟踪终止条件。

  边界描述是指用相关方法和数据来表示区域边界。边界描述中既含有几何信息，也含有丰富的形状信息，是一种很常见的图像目标描述方法。傅里叶描绘子的方法主要利用 DFT描绘子重建区域边界曲线。由于傅里叶的高频分量对应于一些细节部分，而低频分量则对应基本形状，因此，重建时可以只使用复序列的前 M 各较大系数其余置零。

   关于图像分割，就不得不提起经典又传统的分水岭算法了。传统的分水岭分割算法，是一种基于拓扑理论的数学形态学的分割方法，传统的分水岭分割方法，是一种基于拓扑理论的数学形态学的分割方法。传统的分水岭分割方法，是一种基于拓扑理论的数学形态学的分割方法，其基本思想是把图像看作是测地学上的拓扑地貌,图像中每一像素的灰度值表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆地，而集水盆地的边界则形成分水岭。分水岭的概念和形成可以通过模拟浸入过程来说明。在每-一个局部极小值表面，刺穿一个小孔，然后把整个模型慢慢浸人水中，随着浸入的加深, 极小值表面，每一个局部极小值的影响域慢慢向外扩展，在两个集水盆地汇合处构筑大坝如下每一个局部极小值的影响域慢慢向外扩展，在两个集水盆地汇合处构筑大坝如下图所示，即形成分水岭。分水岭变换通过不同的水系排水来分离区域，达到图像图所示，即形成分水岭.分水岭变换通过不同的水系排水来分离区域，达到图像分割的目的。

五、参考代码及扩展代码流程图

(1)参考代码流程图

 

(2)扩展代码流程图

 

六、参考代码

参考代码中实现了图像的阈值分割、数学形态学滤波、边缘跟踪、傅里叶描绘子计算及

重建。

Image1=im2double(imread('plane.jpg'));
gray=rgb2gray(Image1);
T=graythresh(gray);%使用 Otsu 方法获取阈值，T 被归一化到[0,1]区间。
BW=im2bw(gray,T);%以 T 为阈值把灰度图像 I 转变为二值图像。
figure,imshow(BW),title('二值化图像');
SE=strel('square',3);%创建一个由square指定的结构元素，参数3控制 SE 的大小。
Morph=imopen(BW,SE); %对图像BW进行开运算，返回图像为Morph，SE是结构元素
Morph=imclose(Morph,SE);
figure,imshow(Morph),title('形态学滤波');
[B L]=bwboundaries(1-Morph);%搜索二值图像BW的外边界和内边界
figure,imshow(L),title('划分的区域');
hold on;
for i=1:length(B)
 boundary=B{i};
 plot(boundary(:,2),boundary(:,1),'r','LineWidth',2);
end
M=zeros(length(B)); 
for k=1:length(B) 
 N=length(B{k}); 
 if N/2~=round(N/2) 
 B{k}(end+1,:)=B{k}(end,:); 
 N=N+1;
 end
 M(k)=[N*3/4]; 
end
S=zeros(size(Morph)); 
figure,imshow(S);
hold on;
for k=1:length(B) 
 z=B{k}(:,2)+1i*B{k}(:,1); 
 Z=fft(z); 
 [Y I]=sort(abs(Z)); 
 for count=1:M(k) 
 Z(I(count))=0; 
 end
 zz=ifft(Z);%对Z进行IDFT 运算。 
 plot(real(zz),imag(zz),'w'); 
end

程序运行效果如下：

 

七、实验要求

1. 熟悉 Matlab 函数，读懂参考代码；

2. 拓展内容：

（1）尝试不同的阈值选择方法，实现灰度图像二值化

代码：

I=imread('plane.jpg');
%人工选定阈值进行分割，选择阈值为150
[width,height]=size(I);
T1=150;
for i=1:width
    for j=1:height
        if(I(i,j)

运行结果：

 

 

（2）变换参数实现形态学滤波，查看滤波效果

代码：

Image1=im2double(imread('plane.jpg'));
gray=rgb2gray(Image1);
T=graythresh(gray);
BW=im2bw(gray,T);
figure,imshow(BW),title('二值化图像');
SE=strel('disk',3);
Morph=imopen(BW,SE);
Morph=imclose(Morph,SE);
figure,imshow(Morph),title('形态学滤波');

运行结果：

 

（3）更改重建边界点数，查看效果

代码：

Image1=im2double(imread('plane.jpg')); 
gray=rgb2gray(Image1); 
T=graythresh(gray); 
BW=im2bw(gray,T); 
[B L]=bwboundaries(1-BW); 
figure,imshow(L),title('划分的区域'); 
hold on; 
for i=1:length(B) 
boundary=B{i}; 
plot(boundary(:,2),boundary(:,1),'r','LineWidth',1); 
end 
M=zeros(length(B),4); 
for k=1:length(B) 
N=length(B{k}); 
if N/2~=round(N/2) 
B{k}(end+1,:)=B{k}(end,:); 
N=N+1; 
end 
M(k,:)=[N/2 N*7/8 N*15/16 N*63/64]; 
end 
S=zeros(size(Morph)); 
for m = 1:4 
figure,imshow(S); 
hold on; 
for k=1:length(B) 
z=B{k}(:,2)+1i*B{k}(:,1);Z=fft(z); 
[Y I]=sort(abs(Z)); 
for count=1:M(k,m) 
Z(I(count))=0; 
end 
zz=ifft(Z); 
plot(real(zz),imag(zz),'w'); 
end 
end 

运行结果：

 

（4）自行设计方法实现图像分割，并计算分割区域相关参数

代码：

img=imread('plane.jpg');
subplot(2,3,1);
imshow(img);
C = makecform('srgb2lab');       %设置转换格式
img_lab = applycform(img, C);
 
ab = double(img_lab(:,:,2:3));    %取出lab空间的a分量和b分量
nrows = size(ab,1);
ncols = size(ab,2);
ab = reshape(ab,nrows*ncols,2);
 
nColors = 3;        %分割的区域个数为3
[cluster_idx cluster_center] = kmeans(ab,nColors,'distance','sqEuclidean','Replicates',3);  %重复聚类3次
pixel_labels = reshape(cluster_idx,nrows,ncols);
subplot(2,3,2);
imshow(pixel_labels,[]), title('聚类结果');
 
 
%显示分割后的各个区域
segmented_images = cell(1,3);
rgb_label = repmat(pixel_labels,[1 1 3]);
 
for k = 1:nColors
    color = img;
    color(rgb_label ~= k) = 0;
    segmented_images{k} = color;
end
subplot(2,3,3);
imshow(segmented_images{1}), title('分割结果——区域1');
subplot(2,3,4);
imshow(segmented_images{2}), title('分割结果——区域2');
subplot(2,3,5);
imshow(segmented_images{3}), title('分割结果——区域3');

运行结果：