数字图像处理技术与应用练习题
说明:不允许直接使用MATLAB(或者OPENCV等)所带的图像处理函数,重点考察大家是否理解了各种处理算法,算法可用伪代码描述。算法应较详细。
图像的几何变换
图像放大缩小
设一幅大小为M×N的灰度图像I中,现要变成(放大或缩小)为 P×Q的图像J,请写出J的生成算法(要求使用双线性插值)。
算法思路:
在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在X和Y两个方向分别进行一次线性插值。如果选择一个坐标系统使得 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简。
图像的空间变换,也称几何变换或几何运算,包括图像的平移、旋转、镜像变换、转置、缩放等。空间变换可如下表示:设(u,v)为源图像上的点,(x,y)为目标图像上的点,则空间变换就是将源图像上(u,v)处的颜色值与目标图像上(x,y)处的颜色对应起来。
计算机所处理的图像都是指点阵图,也就是用一个像素矩阵来描述一副图像。 举个简单的图像:3X3 的256级灰度图,也就是高为3个象素,宽也是3个象素的图像,每个象素的取值可以是 0-255,代表该像素的亮度,255代表最亮,也就是白色,0代表最暗,即黑色 。
假如图像的象素矩阵如下所示:(这个矩阵中,图象处理中最常用的坐标系是:x从左到右,从0开始,y从上到下,也是从0开始)
234 38 22
67 44 12
89 65 63
如果想把这副图放大为 4X4大小的图像,那么第一步肯定想到的是先把4X4的矩阵先画出来再说,好了矩阵画出来了,如下所示,当然,矩阵的每个像素都是未知数,等待着我们去填充:
? ? ? ?
? ? ? ?
? ? ? ?
? ? ? ?
然后要往这个空的矩阵里面填值了,要填的值从哪里来来呢?是从源图中来,好,先填写目标图最左上角的象素,坐标为(0,0),那么该坐标对应源图中的坐标可以由如下公式得出:
srcX = dstX * (srcWidth / dstWidth)
srcY = dstY * (srcHeight / dstHeight)
套用公式,就可以找到对应的原图的坐标了
(0*(3/4),0*(3/4))=>(00.75,00.75)=>(0,0)
找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。
接下来,如法炮制,寻找目标图中坐标为(1,0)的象素对应源图中的坐标,套用公式:
(10.75,00.75)=>(0.75,0)
结果发现,得到的坐标里面竟然有小数,这可怎么办?计算机里的图像可是数字图像,象素就是最小单位了,象素的坐标都是整数,从来没有小数坐标。这时候采用的一种策略就是采用四舍五入的方法(也可以采用直接舍掉小数位的方法),把非整数坐标转换成整数,好,那么按照四舍五入的方法就得到坐标(1,0),完整的运算过程就是这样的:
(10.75,00.75)=>(0.75,0)=>(1,0)
那么就可以再填一个象素到目标矩阵中了,同样是把源图中坐标为(1,0)处的像素值38填入目标图中的坐标。
依次填完每个象素,一幅放大后的图像就诞生了,像素矩阵如下所示:
234 38 22 22
67 44 12 12
89 65 63 63
89 65 63 63
这种放大图像的方法叫做最临近插值算法,这是一种最基本、最简单的图像缩放算法,效果也是最不好的,放大后的图像有很严重的马赛克,缩小后的图像有很严重的失真;效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真,比如,当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值,这种方法是很不科学的,当推得坐标值为 0.75的时候,不应该就简单的取为1,既然是0.75,比1要小0.25 ,比0要大0.75 ,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的,这样才能达到更好的缩放效果。
双线型内插值算法就是一种比较好的图像缩放算法,它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,因此缩放效果比简单的最邻近插值要好很多,计算量比零阶插值大,但缩放后图像质量高,不会出现像素值不连续的情况。
双线性内插值算法描述如下:
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数),则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)
其中f(i,j)表示源图像(i,j)处的的像素值,以此类推。
假如目标图的象素坐标为(1,1),那么反推得到的对应于源图的坐标是(0.75 , 0.75), 这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素(1,1)的取值不能够由这个虚拟象素来决定,而只能由源图的这四个象素共同决定:(0,0)(0,1)(1,0)(1,1),而由于(0.75,0.75)离(1,1)要更近一些,那么(1,1)所起的决定作用更大一些,这从公式1中的系数uv=0.75×0.75就可以体现出来,而(0.75,0.75)离(0,0)最远,所以(0,0)所起的决定作用就要小一些,公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点;
算法具体步骤如下:
假设原始图像大小为size=m×n,其中m与n分别是原始图像的行数与列数。若图像的缩放因子是t(t>0),则目标图像的大小size=t×m×t×n。对于目标图像的某个像素点P(x,y)通过P*1/t可得到对应的原始图像坐标P’( x1,y1),其中x1=x/t,y1=y/t,由于x1,y1都不是整数所以并不存在这样的点,这样可以找出与它相邻的四个点的灰度f1、f2、f3、f4,使用双线性插值算法就可以得到这个像素点P’(x1,y1)的灰度,也就是像素点P(x,y)的灰度。
一个完整的双线性插值算法可描述如下:
(1)通过原始图像和比例因子得到新图像的大小,并创建新图像。
(2)由新图像的某个像素(x,y)映射到原始图像(x’,y’)处。
(3)对x’,y’向下取整得到(xx,yy)并得到(xx,yy)、(xx+1,yy)、(xx,yy+1)和(xx+1,yy+1)的值。
(4)利用双线性插值计算公式得到像素点(x,y)的值并写回新图像。
(5)重复步骤(2)直到新图像的所有像素写完。
图像旋转
设一幅大小为M×N的灰度图像I中,现要将其逆时针旋转 A度,得到图像J,请写出J的生成算法(要求使用近邻插值)。
旋转变换,可以看成是在一个橡皮膜上印刷一副图像,然后根据预定的一组规则拉伸该薄膜,包括两个基本操作:(1)坐标的空间变换(2)灰度内插,即对空间变换后的像素赋灰度值。此处采用近邻插值法,将图像中近邻的灰度赋给每个新的位置。
坐标变换可由下式表示:

其中(v,w)是原图像中像素的坐标,(x,y)是变换后图像像素的坐标。用于旋转变换的空间坐标变换如下:

①
而数学坐标系和图像坐标系不
同,当对图像进行旋转时,图像以自身中心为 原点建立坐标系,即数学坐标系,图像坐标系确是以图像左上角为原点,则 需要进行坐标系的变换。总体的变换步骤为:
(1)先将原图的图像坐标系转换为数学坐标系,变换如公式②,(2)在数学坐 标系下使用旋 转坐标变换矩阵①进行旋转计算(3)将旋转后的图像的数 学坐标转回图像 坐 标,变换如公式③。

②

③
其中,m表示宽,n表示高,m’表示旋转后图像宽,n’表示旋转后图像高。
最终的公式变换如下:

坐标变换后,扫描图像,对于图像中灰度为0的点按照近邻插值法进行赋值。
代码如下:
im1=imread('user.png');
[m,n,p]=size(im1);
a=0.5;
%a=sin30=0.5
b=0.866;
%b=cos30=0.866
row=n*a+m*b;
col=n*b+m*a;
for i=1:row
for j=1:col
%对新坐标赋0值
im2(i,j,:)=uint8(0);
end
end
for i=1:m
for j=1:n
%根据公式计算新坐标
x_=round(abs((i-m/2)*b-(j-n/2)*a+row/2));
y_=round(abs((i-m/2)*a+(j-n/2)*b+col/2));
for k=1:3
im2(x_,y_,k)=im1(i,j,k);
end
end
end
temp1=uint8(0);
temp2=uint8(0);
temp3=uint8(0);
for i=1:row
temp1=uint8(0);
temp2=uint8(0);
temp3=uint8(0);
for j=1:col
if(im2(i,j,:)==uint8(0))
else
kk=j;
end
end
for j=1:kk
if(im2(i,j,:)==uint8(0))
im2(i,j,1)=temp1;
im2(i,j,2)=temp2;
im2(i,j,3)=temp3;
else
temp1=im2(i,j,1);
temp2=im2(i,j,2);
temp3=im2(i,j,3);
end
end
end
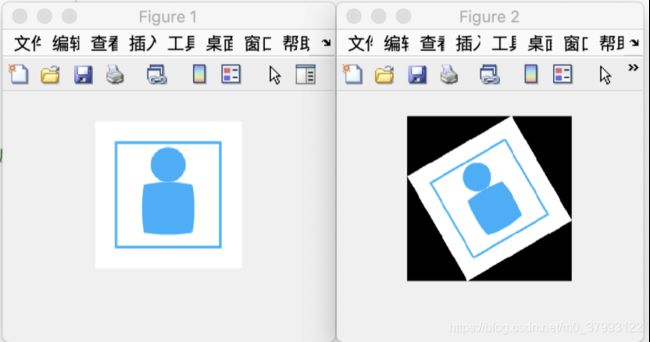
imshow(im1);
figure;
imwrite(im1,'5.png');
imshow(im2);
imwrite(im2,'6.png');
图像灰度变换
直方图均衡化
设一幅大小为M×N的灰度图像I中,灰度为g的像素数为h(g), 。 请写出对图像I进行直方图均衡化,得到图像J的计算方法。

- 统计原图像直方图
- 计算新的灰度级,修正sk为合理灰度级
- 计算新的直方图
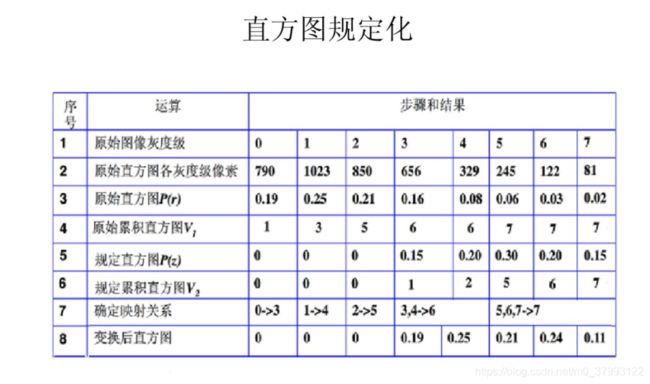
直方图规定化
设一幅大小为M×N的灰度图像I中,灰度为g的像素数为h(g), 。另给定一个直方图t(g),。 请写出对图像I进行变换的方法,使得变换后的新图像的直方图与t相同(近似相等)。
直方图的规定划的方法步骤:
根据直方图t(g)可以知道概率密度Pz(z),则对图像I进行变换的步骤如下:
(1)由输入图像得到Pg(g),并由式子①求得S的值
(2)由式子②,根据直方图t(g)得到的概率密度Pz(z)得到G(z)
(3)求得反变换函数,因为Z是由S得到的,所以该处理是S到Z的映射,而后者正是我们期望的值
(4)首先用式①对输入图像进行均衡得到输出图像,该图像的像素值是s值,对均衡后的图像中具有S值的每个像素执行反映射,得到输出图像中的相应像素,当所有像素处理完成后,输出图像就可以得到给定直方图t(g)
代码如下:
clear all;
close all;
orgin=imread('woman.png');
orgin=rgb2gray(orgin);
[m_o,n_o]=size(orgin);
orgin_hist=imhist(orgin)/(m_o*n_o);
standard = imread('man.png');
standard=rgb2gray(standard);
[m_s,n_s]=size(standard);
standard_hist=imhist(standard)/(m_s*n_s);
startdard_value=[];
orgin_value=[];
for i=1:256
startdard_value=[startdard_value sum(standard_hist(1:i))];
orgin_value=[orgin_value sum(orgin_hist(1:i))];
end
for i=1:256
value{i}=startdard_value-orgin_value(i);
value{i}=abs(value{i});
[temp index(i)]=min(value{i});
end
newimg=zeros(m_o,n_o);
for i=1:m_o
for j=1:n_o
newimg(i,j)=index(orgin(i,j)+1)-1;
end
end
newimg=uint8(newimg);
subplot(2,3,1);imshow(orgin);title(‘灰度图像I’);
subplot(2,3,2);imshow(standard);title(‘给定图’');
subplot(2,3,3);imshow(newimg);title(‘规范化后图像’);
subplot(2,3,4);imhist(orgin);
title(‘图像I直方图’);
subplot(2,3,5);imhist(standard);
title('给定直方图t(g)');
subplot(2,3,6);imhist(newimg);
title(‘新图像直方图’);
图像灰度的分段线性拉伸
对一幅灰度图像,给出灰度分段线性变换方法,使得新图像中 5%的像素的灰度变为0, 5%的像素灰度变为255。
分段线性变换有很多种, 包括灰度拉伸、 灰度窗口变换等, 本节仅讲述最为常用的灰度拉伸.
利用分段线性变换函数来增强图像对比度的方法实际是增强原图各部分的反差,即增强输入图像中感兴趣的灰度区域,相对抑制那些不感兴趣的灰度区域。分段线性函数的主要优势在于它的形式可任意合成,而其缺点是需要更多的用户输入.
分段的灰度拉伸可以更加灵活地控制输出灰度直方图的分布,可以有选择的拉伸某段灰 请写出生成 (2N+1)×(2N+1)大小的高斯模板H(方差为sigma)的方法。 请写出使用大小为(2N+1)×(2N+1)模板H对图像I进行滤波,生成图像J的方法。 请写出使用大小为3×3的模板对图像I进行中值滤波,生成图像J的方法。 举一个简单的例子:一维序列{0,3,4,0,7},进行中值滤波排序后为{0,0,3,4,7},则其中值为3。 试简述中值滤波的特性和适用场合。 信号处理时经常要做的一件事就是滤波,其中线性滤波器比如FIR、IIR 等类型都是研究的比较透彻的,实际使用中也有很好的效果。但是有时我们遇到的信号的噪声比较顽固,比如说电子信号中的爆米花噪声(popcorn noise)还有图像处理中的椒盐噪声(salt-and-pepper noise),用普通的线性滤波器只能将其压低,而无法彻底消除。这时一些非线性滤波器就体现出优势来了。比如说今天要介绍的中值滤波器。 窗开的越大,输出的结果就越平滑,但也可能会把我们有用的信号特征给抹掉。所以窗的大小要根据实际的信号和噪声特性来确定。 最大最小值滤波是一种比较保守的图像处理手段,与中值滤波类似,首先要排序周围像素和中心像素值,然后将中心像素值与最小和最大像素值比较,如果比最小值小,则替换中心像 特别说明一点的是,均值滤波对于高斯噪声的效果比较好,中值滤波对于椒盐噪声的效果比较好 写出二维离散傅立叶变换、反变换的计算公式。 频域滤波由修改一幅图像的傅里叶变换然后计算其反变换得到处理后的结果组成,由此给定一幅大小MxN的数字图像f(x,y),基本滤波公式如下: 其中F^(-1)是IDFT,即傅里叶反变换,F(u,v)是输入图像f(x,y)的DFT,即傅里叶变换,H(u,v)是滤波函数,g(x,y)是滤波后输出的图像。正反变换公式如下: 则基本的步骤为: (1)给定一幅大小为MxN的输入图像f(x,y),首先得到填充参数P和Q,可以选择P=2M,Q=2N 代码如下: 请写出求 Otsu阈值(即最大类间距准则)的计算方法。 求类间方差: OTSU算法的假设是存在阈值TH将图像所有像素分为两类C1(小于TH)和C2(大于TH),则这两类像素各自的均值就为m1、m2,图像全局均值为mG。同时像素被分为C1和C2类的概率分别为p1、p2。因此就有: 请写出C 均值(K-means)聚类分割的基本步骤。 C-means,常称作K-means算法,是基于距离的聚类算法。采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。其基本思想:取定c 类,选取c 个初始聚类中心即 , 即代表点 。按最小距离原则将各样本分配到离代表点最近的一类中 ,不断重新计算类中心 , 调整 各样本类别,最终使聚类准则函数 Je 最小。算法采用误差平方和准则函数作为聚类准则函数。 ①用样本间的距离(欧式距离)作为相似性度量 K-means 是一种将输入数据划分成 k 个簇的简单的聚类算法。K-means 反复提炼初始评估的类中心。 k-means算法中的k代表类簇个数,means代表类簇内数据对象的均值(这种均值是一种对类簇中心的描述),因此,k-means算法又称为k-均值算法。k-means算法是一种基于划分的聚类算法,以距离作为数据对象间相似性度量的标准,即数据对象间的距离越小,则它们的相似性越高,则它们越有可能在同一个类簇。 距离的度量:聚类简单理解就是把相似的东西聚到一起,如何判断两个样本点是不是相似的呢,这个就要根据距离做判断,最常见的计算方式就是欧几里得距离(直接算两个点的欧式距离)和余弦相似度(先标准化),当使用欧式距离的时候,先要对数据进行标准化, 什么是标准化:比如现在有两个维度,x轴,y轴,x轴数据0.01,0.02,0.04,y轴数据100,200,300,当计算相似度的时候,x轴的差异无论怎么算都比较小,y轴的差异无论怎么算都比较大,那样我们潜意识里就认为相似度主要由y轴决定,实际算出来也是这样,所以说,在使用距离的度量的时候,基本情况下,都要对所有数据进行标准化,比如让x轴取值范围在0到1之间,y轴取值范围在0到1之间,让数据x和y基本在一个比较小的范围内浮动,比如说都是0到1,或者-1到1。 先把数据做标准化,然后再用距离的度量看一下什么样的两个样本点是相似的,再把相似的分到一簇。 步骤如下: xj 是输入数据,并且是矢量。该算法是启发式提炼算法,在很多情形下都适用,但 1、高斯平滑(略) 进一步可以得到图像梯度的幅值: 3、根据角度对幅值进行非极大值抑制 量化化情况可总结为: 在每一点上,领域中心 x 与沿着其对应的梯度方向的两个像素相比,若中心像素为最大值,则保留,否则中心置0,这样可以抑制非极大值,保留局部梯度最大的点,以得到细化的边缘。 设有一幅二值图像(元素取值为0或1),请生成该图像的标记图像。(即第一个连通区域中的每一个白色像素的值都置为1,第二个连通区域中的每一个白色像素的值都置为2,依此类推。区域编号可不考虑顺序) 区域标记有两种算法,一种是一次扫描算法,一种是二次扫描算法。 算法代码如下: 设一幅二值图像中,只有一个白色区域,试给出求该区域外围轮廓线的方法(要求按顺时针的顺序给出各点的坐标,即行/列号)。 此题为二值图像,且只有一个白色区域,边界已知,轮廓封闭,算法如下: 正规答案: 算法代码如下: 效果图片如下: 设有一幅二值图像,采用 3×3的结构元(每个元素均为1)对其进行腐蚀操作,试写出得到结果图像的方法。 对Z中的集合A和B,B对A进行腐蚀的整个过程如下: 试写出孔洞填充的算法。对二值图像中所有被白色区域包围(封闭)的黑色像素即为孔洞。 算法流程: 设有两个白色区域,被一条细小的白线所连接,试设计一种算法,消除两个区域之间的细线,使两个区域分开。 第1步: 使用区域距离变换算子获取距离信息图 距离变换简化了分水岭算法的复杂度。距离变换针对二值图像,目标像素为1,背景像素为0。距离变换的结果图像是一个灰度图像,灰度值就是图像中该像素距离其最近的背景像素的距离。 假设两个像素点P1(x1,y1),P2(x2,y2) 距离D = sqrt((x1-x2)(x1-x2) + (y1-y2)(y1-y2)) 第2步: 使用阈值分水岭算子获取盆地 第3步: 则分割结果为: 2.程序使用的算子 4.算法思路 (1)简单的阈值分割; (2)计算连通域connection; (3)基于距离变换的分水岭区域分割,使用算子distance_tansform,watersheds (4)盆地与原连通域求交集,分离粘连颗粒; 计算包围给定点集的最小凸多变形。 大概判断过程: k=4,向前倒查,p1与p4在Pk-1Pk-2两侧,所以p3不在凸壳边界上,删去p3,原p4成为p3,之后p1和p4在Pk-1Pk-2同侧,p3暂时在边界上,继续查下去,最后可以得到凸壳的6个顶点 2,删去p3,p4,…,pn-1中不是凸壳上的点,方法如下: begin 1 k = 4 2 j = 2 3 if P1 和 Pk 分别在线段Pk-j+1 Pk-j两侧 then 删去 Pk-1,后继顶点编号减1,k = k-1,j = j-1 else Pk-1暂为凸壳顶点,并记录 4 j = j+1 ,go to 3,直到 j = k-1 5 k = k+1,go to 2,直到 k = n+1//注意,因为节点编号随着节点的删除是在不断减少的,所以在算法过程中n也是在不断减少的 end 3,顺序输出凸壳顶点 其中:判断两点在某一个线段两侧还是同侧,用向量叉乘就行了 比如说有两点p,q,线段AB则计算向量pA,pB,qA,qB;在计算叉乘pApB,qAqB如果同号说明在线段同侧,否则在异侧!另外如果计算出现零,则说明那一点在那个线段上,即出现多点共线的情况 算法分析:由于点集有n个点,步骤2中转移到2的次数不会超过n,每一个顶点至多删去1次,删去顶点的个数也不可能超过n。因此步骤2是线性时间复杂度;步骤1很显然涉及到角度的排序问题,为O(nlogn)复杂度;所以总共需要O(nlogn)时间,此算法为最优算法!因为可以证明凸壳的最优算法的下界就是OMIGA(nlogn) 如何判断一个点在多边形内部? 射线法 这里有二种特殊情况: 我们可以把多边形可以看做是一条从某点出发的闭合路,可以观察到在内部的点永远都在路的同一边。 算法描述: 首先给出有序边表法中定义使用的变量。 基本思想:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。 算法描述: 建立边表的方法: 算法流程: 点填充有好几种方法,其中比较简单实现的是四连通泛填充算法。基本思路就是给定种子,然后去填充种子上下左右四个方向的像素点,如果为空,则进行填充。
度区间以改善输出图像。如果一幅图像灰度集中在较暗的区域而导致图像偏暗,我们可以用
灰度拉伸功能来扩展(斜率>1)物体灰度区间以改善图像:同样,如果图像灰度集中在较亮
的区域而导致图像偏亮,也可以用灰度拉伸功能来压缩〈斜率<1)物体灰度区间以改善图像
质量。
灰度拉伸是通过控制输出图像中灰度级的展开程度来达到控制对比度的效果。一般情况
下都限制x1空域线性滤波
高斯模板生成
% 本程序目的在生成自己的高斯模板%
公式: p(z) = exp(-(z-u)^2/(2*d^2) / (sqrt(2*pi)*d)
clear all;close all;clc;
size = 3;
sigma = 0.5;
% size为模板大小% sigma为标准差
%计算高斯模板的中心位置
siz = ( [size size] - 1 ) / 2;
sig = sigma;
%用meshgrid是为了加速,不用for循环
[x y] = meshgrid(-siz(): siz(1),-siz(2): siz(2));
% 相当于围绕中心点(0,0)产生各个点的坐标,之后再根据坐标代公式得到各个点具体值
% 计算exp(-(x^2 + y^2)/(2 * sig^2))
arg = -( x .* x + y .* y) ./ (2 * sig * sig);
h = exp(arg);
h( h < eps * max( h(:) ) ) = 0;
% 求和,用来归一化
sumh = sum( h(:) );
% 防止求和之后出现为0的情况,然后再归一化一下使高斯,模板为小数
if sumh ~= 0
h = h / sumh;
end
线性滤波
设计一个能够对图像进行平滑的线性滤波器(模板)。
平滑则九宫格数值相同
设计一个能够对图像进行锐化的线性滤波器(模板)。
锐化则九宫格中心为负

空域非线性滤波
中值滤波
算法描述:
[1] 获得源图像的首地址及图像的宽和高
[2] 开辟一块内存缓冲区,用以暂存结果图像,并初始化为0
[3] 逐个扫描图像中的像素点,将其邻域各元素的像素值从小到大进行排序,将求得到的中间值赋值给目标图像中与当前点对应的像素点
[4] 循环步骤[3],直到处理完源图像的全部像素点
[5] 将结果从内存缓冲区复制到源图像的数据区
所谓中值滤波,其中滤波就是前面讲的去噪,关键在于中值两字,中值从字面意思上讲就是中间的那个值也就是中心值。
数字图像是以二维图像来描述的,故对图像的滤波也就是对二维数据序列的滤波,这个二维序列相当于一个二维矩阵,里面元素的值就是每个像素点的像素。
中值滤波通常采用一个含奇数个点的滑动窗口,用窗口中的灰度值的中值来代替中心点的灰度值,其实就是对这个窗口中的灰度值进行排序,然后将其中值赋值给中心点即可。常用的中值滤波窗口形状有线状、方形、圆形以及十字形等。
注:对每一个像素的m*n邻域进行计算,中值滤波对图像的边界用0做扩张,所以对边界可能会出现扭曲。中值滤波的特性
设计一个能保持图像中细小尺寸的边缘(如线状目标)的滤波方法。
中值滤波器在图像处理领域用的比较多,其实这种滤波器也可以用于一维信号,有时甚至能起到意想不到的效果。
中值滤波器的想法很简单,如果一个信号是平缓变化的,那么某一点的输出值可以用这点的某个大小的邻域内的所有值的统计中值来代替。这个邻域在信号处理领域称之为窗(window)。统计排序滤波
最大值滤波的实现方法是什么?使用最大值滤波会产生何种效果?
素为最小值,如果中心像素比最大值大,则替换中心像素为最大值。一个Kernel矩阵为3X3的最大最小值滤波如下:
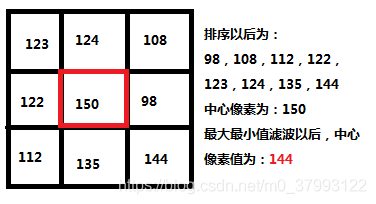
最小值滤波的实现方法是什么?使用最小值滤波会产生何种效果?
频域滤波
傅里叶变换
![]()

基于频域滤波的基本步骤
写出基于频域的低通滤波的步骤。
(2)对f(x,y)添加必要数量的0.形成大小为PxQ的填充后的图像fp(x,y)
(3)用(-1)^(x+y)乘以fp(x,y)移到其变换的中心
(4)计算来自步骤3当中的图像的傅里叶变换,得到F(u,v)
(5)生成一个实的、对称的滤波函数H(u,v),其大小为PxQ,中心在(P/2,Q/2)处,用陈列相乘形成乘积G(u,v)=H(u,v)F(u,v);即G(i,k)=H(i,k)F(i,k)
(6)得到处理后的图像
={real[F^(-1)[G(u,v)]]}
为了忽略由于计算不准确导(-1)^(x+y)致的寄生复变量,选择了实部。
(7)通过从的左上象限提取MxN区域,得到最终的处理结果g(x,y)clear all;
close all;
clc;
img_origin=imread('man.png');
img_origin=rgb2gray(img_origin);
d0=50;
img_noise=imnoise(img_origin,'salt');
img_f=fftshift(fft2(double(img_noise)));
[m n]=size(img_f);
m_mid=fix(m/2);
n_mid=fix(n/2);
img_lpf=zeros(m,n);
for i=1:m
for j=1:n
d=sqrt((i-m_mid)^2+(j-n_mid)^2);
if d<=d0
h(i,j)=1;
else
h(i,j)=0;
end
img_lpf(i,j)=h(i,j)*img_f(i,j);
end
end
img_lpf=ifftshift(img_lpf);
img_lpf=uint8(real(ifft2(img_lpf)));
subplot(2,2,1);imshow(img_origin);title(‘给定图像’);
subplot(2,2,2);imshow(img_noise);title('噪声图'');
subplot(2,2,3);imshow(img_lpf);title(‘傅里叶低通滤波’);
图像分割
Otsu阈值分割
试证明采用最大类间距准则计算出的阈值与采用最小类内距准则计算出的阈值相同。
p1m1+p2m2=mG (1)
p1+p2=1 (2)
根据方差的概念,类间方差表达式为:
![]()
(3)
我们把上式化简,将式(1)代入式(3),可得:
![]()
(4)
其实求能使得上式最大化的灰度级 k 就是OTSU阈值了,很多博客也是这样做的。
其中:
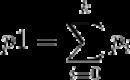
(5) 
(6)
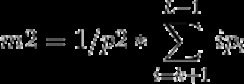
(7)
照着公式,遍历0~255个灰度级,求出使式(4)最大的 k 就ok了。K-means 聚类分割
算法原理
②用各类样本与类均值间的平方误差和作为聚类准则
定义准则函数:
,其中:
是常用的聚类准则函数 , 表示N个样本聚类成c 类时,所产生的总误差的平方和 , 其值取决于c 个聚类中心。
(1) 以随机或猜测的方式初始化类中心 ui,i=1…k;
(2) 将每个数据点归并到离它距离最近的类中心所属的类 ci;
(3) 对所有属于该类的数据点求平均,将平均值作为新的类中心;
(4) 重复步骤(2)和步骤(3)直到收敛。
K-means 试图使类内总方差最小:
是并不能保证得到最优的结果。为了避免初始化类中心时没选取好类中心初值所造成的影响,该算法通常会初始化不同的类中心进行多次运算,然后选择方差 V 最小的结果。边缘检测
请写出Canny算子检测边缘的详细步骤。
2、计算梯度幅度和方向
可选用的模板:soble算子、Prewitt算子、Roberts模板等等;
一般采用soble算子,OpenCV也是如此,利用soble水平和垂直算子与输入图像卷积计算dx、dy:
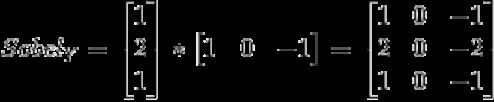
=
为了简化计算,幅值也可以作如下近似:
角度为:
如下图表示了中心点的梯度向量、方位角以及边缘方向(任一点的边缘与梯度向量正交) :
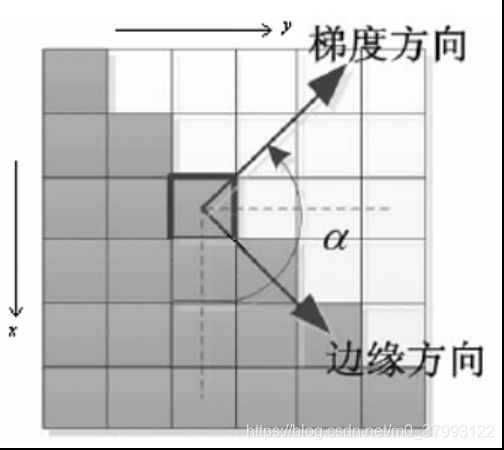
划重点:是沿着梯度方向对幅值进行非极大值抑制,而非边缘方向,这里初学者容易弄混。
例如:3*3区域内,边缘可以划分为垂直、水平、45°、135°4个方向,同样,梯度反向也为四个方向(与边缘方向正交)。因此为了进行非极大值,将所有可能的方向量化为4个方向,如下图:

非极大值抑制即为沿着上述4种类型的梯度方向,比较3*3邻域内对应邻域值的大小:4、用双阈值算法检测和连接边缘
形态运算
区域标记
一次扫描算法思路如下
(1)先将图像转为0,1的二值图像
(2)遍历图像,将为1的像素点在标记图像中用标号标记,用元组模拟队列,将此像素点坐标入队
(3)遍历已经入队的元素,进行八领域搜索,如果当前像素领域为1并且标记图像中的领域没有标记则标记该坐标位置。
二次扫描算法思路如下:
(1)第一次扫描,将0视为背景像素,1为目标像素。从左到右从上到下一次扫描,背景像素保持0不变,遇到1时,分析它的八领域。如果四个方向都是0,则该位置创建一个新的标号,在原标号上加1,如果四个方向的非零值,即标号都一样,则该位置的标号就是这个非零标号,如果四个方向的非零值有两个不同的标号,则该位置就选择其中之一,并记录两个不同标号
(2)第二次扫描时,合并相同的标号,并得到结果。clear all;
close all;
clc;
img=imread('liantong.jpg');
s=im2bw(img,0.5);
imshow(mat2gray(s));
[m n]=size(s);
tmp=zeros(m,n);
label=1;
queue_h=1;
queue_t=1;
neighbour=[-1 -1;-1 0;-1 1;0 -1;0 1;1 -1;1 0;1 1];
for i=2:m-1
for j=2:n-1
if s(i,j)==1&&tmp(i,j)==0
tmp(i,j)=label;
q{queue_t}=[i j];
queue_t=queue_t+1;
while queue_h~=queue_t
pix=q{queue_h};
for k=1:8
pix_=pix+neighbour(k,:);
if pix_(1)>=2 && pix_(1)<=m-1 && pix_(2)>=2 && pix_(2)<=n-1
if s(pix_(1),pix_(2))==1 && tmp(pix_(1),pix_(2))==0
tmp(pix_(1),pix_(2))=label;
q{queue_t}=[pix_(1) pix_(2)];
queue_t = queue_t+1;
end
end
end
queue_h = queue_h+1;
end
clear q;
label = label + 1;
queue_h =1;
queue_t =1;
end
end
end
figure,imshow(mat2gray(tmp))
边界跟踪
(1)首先现在图像中找到一个边界点,也就要遍历图像,找到第一个值为255,即白色的像素点。记录该点的坐标。
(2)由于是顺指针给出坐标,初始跟踪方向为右上方方向。
(3)判断该点是否为目标点,是则将该点设置为新的跟踪的起点
(4)将找到该点目标点的方向顺时针旋转90度,作为新的跟踪方向,继续检测新的跟踪方向上的点
(5)若不是目标点,则沿逆时针旋转45度,一直找到目标点
(6)找到目标点后,在当前跟踪方向的基础上,顺时针旋转90度作为新的跟踪方向,用同样的方法跟踪下一个边界点
(7)直到回到起始点时结束,根据所有的边界点绘制出边界图形
1)令起点b0为图像中左上角标记为1的点,用c0表示b0西侧的点,很显然,c0总是背景点。从c0开始按顺时针方向考察b0的8个邻接点,令b表示所遇到的值为1的第一个邻接点,并直接令c1是序列b1之前的点,存储b0和b1的位置,以便在步骤5中使用。
2)令b=b1和c=c1
3)从c开始按顺时针方向行进,令b的8个邻接点为n1,n2,…,n8。找到标为1 的第一个nk
4)令b=bk和c=ck
5)重复步骤3和4,直到b=b0就找到了下一个边界点为b1.
6)当算法停止时,所找到的b点的序列就构成了排列后的边界点的集合。clear;
clc;
img = imread('bianjie.png');
img = rgb2gray(img);
thresh = graythresh(img);
B = im2bw(img,thresh);
[M,N] = size(img);
mark_img = zeros(M,N);
offset_8 = [-1,0;-1,1;0,1;1,1;1,0;1,-1;0,-1;-1,-1];
match_list = [6,7,8,1,2,3,4,5];
[a,b] = find(B==1);
start_point = [a(1),b(1)]
current_point = start_point;
dir = 1;
result = [start_point];
mark = 1
while (max(current_point ~= start_point))||(mark)
temp_point = current_point + offset_8(dir,:)
if (B(temp_point(1),temp_point(2))==1) && (sum(sum(B(temp_point(1)-1:temp_point(1)+1,temp_point(2)-1:temp_point(2)+1)))~=9)
dir = match_list(dir);
current_point = temp_point;
result = [result;current_point];
mark = 0;
else
dir = dir+1;
if dir == 9
dir = 1;
end
end
end
[new_m,new_n] = size(result);
for i = 1:new_m
mark_img(result(i,1),result(i,2)) = 1;
end
figure,imshow(img);
figure,imshow(mark_img);
for i=1:length(result)
disp(result(i,:))
end
左边为原图,右边为轮廓边界

下图为输出的坐标:

图像腐蚀
⑴ 用结构元素B,扫描图像A的每一个像素
⑵ 用结构元素与其覆盖的二值图像做“与”操作
⑶ 如果都为1,结果图像的该像素为1。否则为0
腐蚀处理的结果是使原来的二值图像减小一圈。孔洞填充
1、以原图像的补集作为Mask,用来限制膨胀结果;
2、以带有白色边框的黑色图像为初始Marker,用SE对其进行连续膨胀,直至收敛;
3、最后对Marker取补即得到最终图像,与原图相减可得到填充图像。粘连区域断开
分水岭算法是一种基于拓扑理论的数学形态学的分割方法,基本思想是把图像看做拓扑地貌,图像中的每一点像素的灰度值表示该店的海拔高度,高灰度代表山脉,低灰度代表盆地,每一个局部极小值及其影响区域成为集水盆,而集水盆的边界形成分水岭。
根据第一步分水岭算法分离结果,若盆地部分的灰度< threshold,则被合并到一起。设B1和B2分别为相邻盆地的最小灰度值,W为将盆地分割为两个盆地的最小灰度值。计算凸壳
1,设凸集中y坐标最小的点为p1,把p1同凸集中其他各点用线段连接,并计算这些线段与水平线的夹角。然后按夹角大小及到p1的距离进行词典分类(先按夹角的大小排序,当夹角一样时,按到p1的距离进行排序),得到一个序列p1,p2,…,pn,依次连接这些点,便得到一个多边形。p1点是凸壳边界的起点,p2与pn也必是凸壳的顶点。Pn+1 = P1!还不知道如何插入图片,现在先用如下简陋的图表示一下,按顶点编号连成一个多边形
。6
7 。 。4
。5
8 。 。3
。9 。2
。1
判断一个点是否在一个区域内部
xv= [0 3 3 0 0]; %x坐标
yv= [0 0 3 3 0];%y坐标
x=1.5;
y=1.5;
in=inpolygon(x,y,xv,yv)
plot(xv,yv,x(in),y(in),’.r’,x(in),y(in),’.b’)
第一种是射线法,算法思想非常巧妙:从待判断的点向某一个方向引射线,计算和多边形交点的个数,如果个数是偶数或者0则点在多边形外,如果是奇数,则在多边形内,如下图:
.
给定线段的两个点P0(x0,y0)和P1(x1,y1),目标点P(x,y),它们有如下的关系:
计算(y - y0) (x1 - x0) - (x - x0) (y1 - y0)
如果答案小于0则说明P在线段的右边,大于0则在左边,等于0说明在线段上。
除了上面两种,还有很多方法
比如面积法:就是计算所有边和目标点组成的三角形面积和是否等于总的多边形面积,如果相等,则点在该区域的内部。
这种方法计算量较大,多边形的面积计算也是比较麻烦;
还有夹角法:判断所有边和目标点的夹角和是否为360度,计算量同样很大。给定一个区域的边界点序列,生成该边界包围的区域(或称区域填充)
多边形填充法
(1)将给定多边形输入;
(2)求出多边形的最小包含矩形;
(3)逐点扫描最小矩形的每一点,并判断是否位于多边形内部,从最小点到最大点一次判断,如果在该多边形内部,则将该点上色;
(4)判断位于多边形内部的方法是,过每一点水平向右作射线,与多边形边界求交点,如果交点个数为奇数,则说明该点在多边形内部,偶数则说明在多边形外部。有序边表法
int m_Begin, m_End, m_edgeNumbers, m_Scan;
//求交边集指针,有效边数,当前扫描位置
float m_yMax[N], m_yMin[N], m_Xa[N], m_Dx[N]; //每条边y最大值,y最小值,每条边与扫描线x的交点,每条边斜率倒数
(1)与x轴平行的边不计入;
(2)多边形的顶点分为两大类:一类是局部极值点,另外一类是非极值点。当扫面线与第一类顶点相交时,应看作两个点;而当扫描线与第二类顶点相交时,应视为一个点,对于极值点则要记录两条边;
(3)扫描线按照y轴从低到高顺次记录;
(4)一条边按照y轴的高低记录;
(5)多条边以x轴递增顺序记录;
1、根据给出的多边形顶点坐标,建立NET表,求出顶点坐标中最大y值ymax和最小y值ymin。
2、初始化AET表指针,使它为空。
3、执行下列步骤直至NET和AET都为空.
(1)如NET中的第y类非空,则将其中的所有边取出并插入AET中;
(2)如果有新边插入AET,则对AET中各边排序;
(3)对AET中的边两两配对,(1和2为一对,3和4为一对,…),
将每对边中x坐标按规则取整,获得有效的填充区段,再填充.
(4)将当前扫描线纵坐标y值递值1;
(5)如果AET表中某记录的ymax=yj,则删除该记录 (因为每条边被看作下闭上开的);
(6)对AET中剩下的每一条边的x递增dx,即x’ = x+ dx .
效果如下:

种子填充算法
不过如果运行这一段代码很容易就会导致栈溢出,,,虽然代码简单,但是没法用。
所以更多的是使用扫描线种子填充算法。
算法描述:
1.种子像素入栈。 当栈非空时,重复执行一下操作。
2.栈顶像素出栈。
3.沿扫描线对出栈像素的左右像素进行填充,直到遇到边界像素为止。
4.将上述区间内的最左、最右像素记为x l e f t x_{left}xleft和x r i g h t x_{right}xright
5.在区间[x l e f t x_{left}xleft , x r i g h t x_{right}xright]内检查与当前扫描线相邻的上下两条扫描线是否全为边界像素或已填充的像素,若为非边界和未填充,则把每一区间的最右像素x r i g h t x_{right}xright作为种子像素压入堆栈,重复执行上述操作。
效果如下: