【路径规划】全局路径规划算法——A*算法
文章目录
- 参考资料
- 1. 算法简介
- 2. 算法精讲
-
- 2.1 预处理
- 2.2 开始搜索
- 2.3 继续搜索
- 2.4 确定实际路径
- 3. 算法总结
-
- 3.1 算法步骤
- 3.2 伪代码
- 4. python实现
参考资料
- Introduction to the A* Algorithm
- 路径规划与轨迹跟踪系列算法
- Robotic Motion Planning Lectures
- A星算法详解
- A星寻路算法
- 路径规划之 A* 算法
1. 算法简介
-
A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。广泛应用于室内机器人路径搜索、游戏动画路径搜索等
-
A*算法结合了贪心算法(深度优先)和Dijkstra算法(广度优先),是一种启发式搜索算法。
-
它使用一个路径优劣评价公式为:
f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n)- f(n) 是从初始状态经由状态n到目标状态的代价估计,
- g(n) 是从初始状态到状态n的实际代价,
- h(n) 是从状态n到目标状态的最佳路径的估计代价。
-
A*算法需要维护两个状态表,分别称为
openList表和closeList表。openList表由待考察的节点组成,closeList表由已经考察过的节点组成。
2. 算法精讲
2.1 预处理
如图,假设我们需要从A点到目标点,这两点之间有一堵墙。

首先,我们把地图栅格化,把每一个方格的中心称为节点;这个特殊的方法把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子,它的状态就是可走 (walkalbe) 和不可走 (unwalkable) 。通过计算出从 A 到 目标点需要走过哪些方格,就找到了路径。一旦路径找到了,便从一个方格的中心移动到另一个方格的中心,直至到达目的地。
2.2 开始搜索
一旦我们把搜寻区域简化为一组可以量化的节点后,我们下一步要做的便是查找最短路径。在 A* 中,我们从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标。

- 从起点 A 开始,定义
A为父节点,并把它加入到 open list中。这个 open list 有点像是一个购物单,当然现在 open list 里只有起点 A ,后面会慢慢加入更多的项。 - 如上图所示,父节点
A周围共有8个节点,定义为子节点。将子节点中可达的(reachable)或者可走的(walkable)放入openList中,成为待考察对象。 - 若某个节点既未在openList,也没在closeList中,则表明还未搜索到该节点。
- 初始时, 节点A离自身距离为0,路径完全确定,将其移入closeList中; close list 中的每个方格都是现在不需要再关注的。
- 路径优劣判断依据是移动代价,单步移动代价采取Manhattan 计算方式(即 d = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d=|x_1-x_2|+|y_1-y_2| d=∣x1−x2∣+∣y1−y2∣),即把横向和纵向移动一个节点的代价定义为10。斜向移动代价为14(即 2 \sqrt2 2倍的横向或纵向移动代价)。
- 现在
openList = {B,C,D,E,F,G,H,I}, closeList = {A}
下面我们需要去选择节点A相邻的子节点中移动代价 f f f最小的节点,下面以节点I的计算为例。
- 移动代价评价函数为: f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n)。 f ( n ) f(n) f(n) 是从初始状态经由状态n到目标状态的代价估计, g ( n ) g(n) g(n) 是在状态空间中从初始状态到状态n的实际代价, h ( n ) h(n) h(n) 是从状态n到目标状态的最佳路径的估计代价。
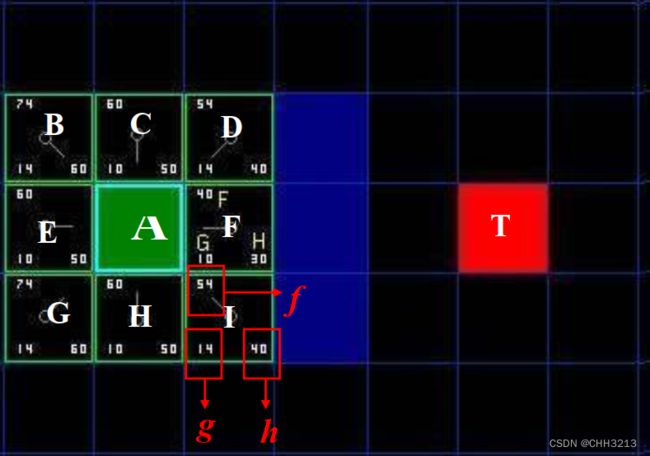
- 首先考察 g g g,由于从
A到该格子是斜向移动,单步移动距离为14,故 g g g = 14. - 再考察估计代价 h h h。估计的含义是指忽略剩下的路径是否包含有障碍物(不可走), 完全按照Manhattan计算方式,计算只做横向或纵向移动的累积代价:横向向右移动3步,纵向向上移动1步,总共4步,故为 h h h = 40.
- 因此从
A节点移动至I节点的总移动代价为: f = g + h = 54 f=g+h=54 f=g+h=54 - 以此类推,分别计算当前openList中余下的7个子节点的移动代价 f f f,从中挑选最小代价节点
F,移到closeList中。 - 现在
openList = {B,C,D,E,G,H,I}, closeList = {A,F}
2.3 继续搜索

- 从openList中选择 f f f值最小的 ( 方格 ) 节点
I(D节点的 f f f值跟I相同,任选其一即可,不过从速度上考虑,选择最后加入 open list 的方格更快。这导致了在寻路过程中,当靠近目标时,优先使用新找到的方格的偏好。 对相同数据的不同对待,只会导致两种版本的 A ∗ A^* A∗ 找到等长的不同路径 ),从 openList里取出,放到 closeList 中。 - 检查所有与它相邻的子节点,忽略不可走 (unwalkable) 的节点、以及忽略已经存在于closeList的节点;如果方格不在openList中,则把它们加入到 openList中,并把它们作为节点
I的子节点 。 - 如果某个相邻的节点(假设为
X)已经在 open list 中,则检查这条路径是否更优,也就是说经由当前节点( 我们选中的节点)到达节点X是否具有更小的 g g g 值。如果没有,不做任何操作。否则,如果 g g g 值更小,则把X的父节点设为当前方格 ,然后重新计算X的 f f f 值和 g g g 值。 - 判断完所有子节点后,现在
openList = {B,C,D,E,G,H,J,K,L}, closeList = {A,F,I} - 依次类推,不断重复。一旦搜索到目标节点
T,完成路径搜索,结束算法。
2.4 确定实际路径
完成路径搜索后,从终点开始,按着箭头向父节点移动,这样就被带回到了起点,这就是搜索后的路径。如下图所示。从起点 A 移动到终点 T就是简单从路径上的一个方格的中心移动到另一个方格的中心,直至目标。

3. 算法总结
3.1 算法步骤
-
首先把起点加入 open list 。
-
重复如下过程:
-
遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
-
把这个节点移到 close list 。
-
对当前方格的 8 个相邻方格:
◆ 如果它是不可抵达的或者它在 close list 中,忽略它;
◆ 如果它不在 open list 中,则把它加入 open list ,并且把当前方格设置为它的父节点,记录该方格的 f , g , h f,g,h f,g,h值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 g g g 值作参考,更小的 g g g 值表示这是更好的路径。如果 g g g值更小,把该节点的父节点设置为当前方格,并重新计算它的 g g g 和 h h h 值。
-
-
停止搜索的情况有两种:
-
把终点加入到了 open list 中,此时路径已经找到了
-
查找终点失败,并且 open list 是空的,此时没有路径。
-
-
保存路径。使用回溯的方法,从终点开始,每个方格沿着父节点移动直至起点,这就是最终搜索到的路径。
3.2 伪代码
初始化open_list和close_list;
* 将起点加入open_list中,并设其移动代价为0;
* 如果open_list不为空,则从open_list中选取移动代价最小的节点n:
* 如果节点n为终点,则:
* 从终点开始逐步追踪parent节点,一直达到起点;
* 返回找到的结果路径,算法结束;
* 如果节点n不是终点,则:
* 将节点n从open_list中移除,并加入close_list中;
* 遍历节点n所有的邻近节点:
* 如果邻近节点m在close_list中,则:
* 跳过,选取下一个邻近节点
* 如果邻近节点m在open_list中,则:
* 计算起点经n到m的g值
* 如果此时计算出来的g值小于原来起点经m的原父节点到m的g值:
* 更新m的父节点为n,重新计算m的移动代价f=g+h
* 否则,跳过
* 如果邻近节点m不在open_list也不在close_list中,则:
* 设置节点m的parent为节点n
* 计算节点m的移动代价f=g+h
* 将节点m加入open_list中
4. python实现
代码实现来自PythonRobotics。
"""
A* grid planning
author: Atsushi Sakai(@Atsushi_twi)
Nikos Kanargias ([email protected])
See Wikipedia article (https://en.wikipedia.org/wiki/A*_search_algorithm)
"""
import math
import matplotlib.pyplot as plt
show_animation = True
class AStarPlanner:
def __init__(self, ox, oy, resolution, rr):
"""
Initialize grid map for a star planning
ox: x position list of Obstacles [m]
oy: y position list of Obstacles [m]
resolution: grid resolution [m],地图的像素
rr: robot radius[m]
"""
self.resolution = resolution
self.rr = rr
self.min_x, self.min_y = 0, 0
self.max_x, self.max_y = 0, 0
self.obstacle_map = None
self.x_width, self.y_width = 0, 0
self.motion = self.get_motion_model()
self.calc_obstacle_map(ox, oy)
class Node:
"""定义搜索区域节点类,每个Node都包含坐标x和y, 移动代价cost和父节点索引。
"""
def __init__(self, x, y, cost, parent_index):
self.x = x # index of grid
self.y = y # index of grid
self.cost = cost
self.parent_index = parent_index
def __str__(self):
return str(self.x) + "," + str(self.y) + "," + str(
self.cost) + "," + str(self.parent_index)
def planning(self, sx, sy, gx, gy):
"""
A star path search
输入起始点和目标点的坐标(sx,sy)和(gx,gy),
最终输出的结果是路径包含的点的坐标集合rx和ry。
input:
s_x: start x position [m]
s_y: start y position [m]
gx: goal x position [m]
gy: goal y position [m]
output:
rx: x position list of the final path
ry: y position list of the final path
"""
start_node = self.Node(self.calc_xy_index(sx, self.min_x),
self.calc_xy_index(sy, self.min_y), 0.0, -1)
goal_node = self.Node(self.calc_xy_index(gx, self.min_x),
self.calc_xy_index(gy, self.min_y), 0.0, -1)
open_set, closed_set = dict(), dict()
open_set[self.calc_grid_index(start_node)] = start_node
while 1:
if len(open_set) == 0:
print("Open set is empty..")
break
c_id = min(
open_set,
key=lambda o: open_set[o].cost + self.calc_heuristic(goal_node, open_set[o]))
current = open_set[c_id]
# show graph
if show_animation: # pragma: no cover
plt.plot(self.calc_grid_position(current.x, self.min_x),
self.calc_grid_position(current.y, self.min_y), "xc")
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect('key_release_event', lambda event: [exit(0) if event.key == 'escape' else None])
if len(closed_set.keys()) % 10 == 0:
plt.pause(0.001)
# 通过追踪当前位置current.x和current.y来动态展示路径寻找
if current.x == goal_node.x and current.y == goal_node.y:
print("Find goal")
goal_node.parent_index = current.parent_index
goal_node.cost = current.cost
break
# Remove the item from the open set
del open_set[c_id]
# Add it to the closed set
closed_set[c_id] = current
# expand_grid search grid based on motion model
for i, _ in enumerate(self.motion):
node = self.Node(current.x + self.motion[i][0],
current.y + self.motion[i][1],
current.cost + self.motion[i][2], c_id)
n_id = self.calc_grid_index(node)
# If the node is not safe, do nothing
if not self.verify_node(node):
continue
if n_id in closed_set:
continue
if n_id not in open_set:
open_set[n_id] = node # discovered a new node
else:
if open_set[n_id].cost > node.cost:
# This path is the best until now. record it
open_set[n_id] = node
rx, ry = self.calc_final_path(goal_node, closed_set)
return rx, ry
def calc_final_path(self, goal_node, closed_set):
# generate final course
rx, ry = [self.calc_grid_position(goal_node.x, self.min_x)], [
self.calc_grid_position(goal_node.y, self.min_y)]
parent_index = goal_node.parent_index
while parent_index != -1:
n = closed_set[parent_index]
rx.append(self.calc_grid_position(n.x, self.min_x))
ry.append(self.calc_grid_position(n.y, self.min_y))
parent_index = n.parent_index
return rx, ry
@staticmethod
def calc_heuristic(n1, n2):
"""计算启发函数
Args:
n1 (_type_): _description_
n2 (_type_): _description_
Returns:
_type_: _description_
"""
w = 1.0 # weight of heuristic
d = w * math.hypot(n1.x - n2.x, n1.y - n2.y)
return d
def calc_grid_position(self, index, min_position):
"""
calc grid position
:param index:
:param min_position:
:return:
"""
pos = index * self.resolution + min_position
return pos
def calc_xy_index(self, position, min_pos):
return round((position - min_pos) / self.resolution)
def calc_grid_index(self, node):
return (node.y - self.min_y) * self.x_width + (node.x - self.min_x)
def verify_node(self, node):
px = self.calc_grid_position(node.x, self.min_x)
py = self.calc_grid_position(node.y, self.min_y)
if px < self.min_x:
return False
elif py < self.min_y:
return False
elif px >= self.max_x:
return False
elif py >= self.max_y:
return False
# collision check
if self.obstacle_map[node.x][node.y]:
return False
return True
def calc_obstacle_map(self, ox, oy):
self.min_x = round(min(ox))
self.min_y = round(min(oy))
self.max_x = round(max(ox))
self.max_y = round(max(oy))
print("min_x:", self.min_x)
print("min_y:", self.min_y)
print("max_x:", self.max_x)
print("max_y:", self.max_y)
self.x_width = round((self.max_x - self.min_x) / self.resolution)
self.y_width = round((self.max_y - self.min_y) / self.resolution)
print("x_width:", self.x_width)
print("y_width:", self.y_width)
# obstacle map generation
self.obstacle_map = [[False for _ in range(self.y_width)]
for _ in range(self.x_width)]
for ix in range(self.x_width):
x = self.calc_grid_position(ix, self.min_x)
for iy in range(self.y_width):
y = self.calc_grid_position(iy, self.min_y)
for iox, ioy in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if d <= self.rr:
self.obstacle_map[ix][iy] = True
break
@staticmethod
def get_motion_model():
# dx, dy, cost
motion = [[1, 0, 1],
[0, 1, 1],
[-1, 0, 1],
[0, -1, 1],
[-1, -1, math.sqrt(2)],
[-1, 1, math.sqrt(2)],
[1, -1, math.sqrt(2)],
[1, 1, math.sqrt(2)]]
return motion
def main():
print(__file__ + " start!!")
# start and goal position
sx = 10.0 # [m]
sy = 10.0 # [m]
gx = 50.0 # [m]
gy = 50.0 # [m]
grid_size = 2.0 # [m]
robot_radius = 1.0 # [m]
# set obstacle positions
ox, oy = [], []
for i in range(-10, 60):
ox.append(i)
oy.append(-10.0)
for i in range(-10, 60):
ox.append(60.0)
oy.append(i)
for i in range(-10, 61):
ox.append(i)
oy.append(60.0)
for i in range(-10, 61):
ox.append(-10.0)
oy.append(i)
for i in range(-10, 40):
ox.append(20.0)
oy.append(i)
for i in range(0, 40):
ox.append(40.0)
oy.append(60.0 - i)
if show_animation: # pragma: no cover
plt.plot(ox, oy, ".k")
plt.plot(sx, sy, "og")
plt.plot(gx, gy, "xb")
plt.grid(True)
plt.axis("equal")
a_star = AStarPlanner(ox, oy, grid_size, robot_radius)
rx, ry = a_star.planning(sx, sy, gx, gy)
if show_animation: # pragma: no cover
plt.plot(rx, ry, "-r")
plt.pause(0.001)
plt.show()
if __name__ == '__main__':
main()