井字棋游戏ai_我创建了一个在井字游戏中击败我的AI
井字棋游戏ai
随时在tic-tac-toe中迷路: https : //www.aaronccwong.com/tic-tac-toe
无耻地取自维基百科。当我一年级的时候,我认为自己是世界上最好的井字游戏选手。 我打败了我的朋友,后者不久前就教我如何打球。 对我来说不幸的是,那种天才的感觉并没有持续很长时间。 我亲爱的朋友,我已经不记得他的名字了,他开始大发脾气。 游戏开始看起来像:
是的 很烂我被毁了。 我回家练习,直到看到一英里远的那些花样。 那时,我并没有想到我实际上是在搜索一棵游戏树,以查看我的举动是否会带来令人满意的结果。
您:那么……什么是游戏树?
我:哦。 它只是游戏的状态空间 ,其中每个节点都是游戏的状态,每个边缘都是有效的移动。
你:
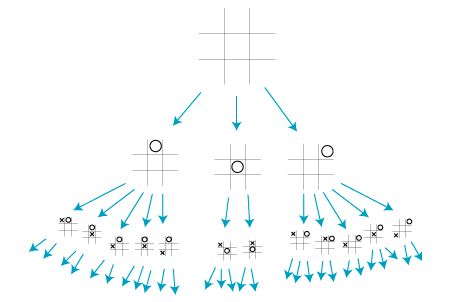
我:对不起。 状态空间是 通过任何动作序列 从 初始状态 可到达的状态集 。 至少这就是罗素和诺维格的定义。 任何游戏的初始状态都是游戏开始时的棋盘状态。 井字游戏的初始状态只是一个3 x 3的网格,其中没有X或O。 然后,每当玩家移动时,游戏就会移动到新状态。 例如,上面O丢失的图像显示5个状态。 进行每个动作后,将达到一个新状态。 所有可达状态的集合是状态空间。 任何需要打破游戏规则才能达到的状态都不会被视为可达到的状态。 因此,带有两个X标记且没有O标记的井字游戏板是无法到达的状态。
不是有效状态。您:这与您创建一个在井字游戏中击败您的AI有什么关系?
我:很简单。 我只是让计算机模拟了每个回合开始时每个可用动作的所有可能结果。 模拟完成后,它会选择导致最佳结果的动作。 这等效于在游戏树中搜索具有最佳结果状态的叶子。
井字游戏的局部游戏树。 感谢加州大学欧文分校的Eppstein教授。随之而来的自然问题是,就成本而言这是否可行。 我们可以回溯进行包络计算,以查看没有太多的状态。 假设计算机先运行。 然后有9种可能的动作。 对于它选择的9个动作中的任何一个,它都必须模拟其他玩家对此做出的动作。 有8种可能的选择。 然后,它又切换回计算机以向左移动7个选择。 一直进行到没有动静为止。 因此,第一步,计算机需要浏览9! = 362,880个州。 在计算机的下一步操作中,还需要标记7个可能的位置,因此计算机需要浏览7个位置! = 5,040个州。 如果我们假设游戏持续到计算机只剩下一个可能的动作,那么计算机就需要浏览9! + 7! + 5! + 3! +1! = 368,047个州。 为了进行比较,国际象棋游戏树有大约10 1 9个节点。
既然我们知道我们可以只看游戏树以找到最佳的移动方式,并且搜索游戏树是可行的,那么哪种算法在这里最有效? minimax算法似乎很自然。
在任何基于回合的两人零和游戏中,您总是试图为自己争取最好的结果,而在大多数情况下,这种结果就是胜利。 这等效于其他玩家达到最糟糕的结果。 同样,如果另一个玩家自己达到了最佳结果,那么这对您来说就是最糟糕的结果,因为您输了。 因此,如果我们让U:State → ℝ为效用函数,那么您的目标将是最大化您在游戏结束时获得的效用,而您的对手的目标将是通过最大化她的效用来最小化您的效用。
假设我们正在与一个理性的对手打交道,最小最大算法将给定玩家回合的每一步的最大效用最大化。
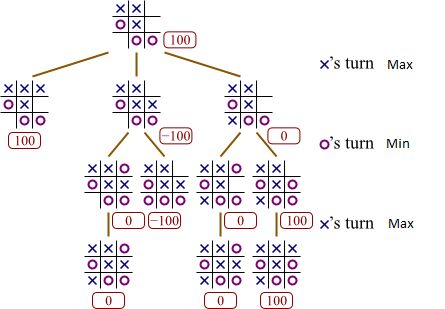
为了更清楚地了解minimax算法的功能,请看上图。 假设获胜给我们的效用为100,输给我们的效用为-100,平局给我们的效用为0。 我们可以打右上角并获胜,可以给我们提供100的效用,但让我们将其他两种情况视为思想练习。
假设我们选择中间行中的未平仓头寸。 然后轮到O了,因为我们假设它是一个理性的对手,所以O将选择扮演最小化我们的效用的位置。 如果O扮演右上角,则我们的效用为0,如果O扮演左下角,则O获胜,因此我们的效用为-100。 因此,我们知道O将打左下角,因此我们知道如果我们打中排,则效用为-100。
同样,如果我们不是打中间排,而是打左下角而不是中间排,那么O将有两个选择。 如果O扮演中间位置,那么我们可以通过打最后一个空位来获胜。 O不需要这个。 O看到,如果她扮演右上角而不是领带,那么我们得到的效用为0。由于这使我们的效用最小,所以O会扮演右上角。 因此,如果我们打左下角,那么我们知道游戏最终将打成平局,并且效用为0。
从分析中可以明显看出,在这三个动作中,打右上角将给我们最大的用处。 因此,作为理性的代理人,这就是我们选择采取的行动。
让UTILITY(state)返回当前状态的实用程序。 令ACTIONS(state)为当前状态下所有有效动作的列表。 令RESULT(state, action)为在当前状态下执行给定操作后的结果状态。 则maxmax算法由下式给出
MINIMAX(s)
For every a ∊ Actions(s)
if MIN-VALUE(RESULT(s, a)) > UTILITY(RESULT(s, best))
best = a
return best
MIN-VALUE(s)
If GAME-OVER(s)
return UTILITY(s)
For every a ∊ Actions(s)
sim-utility = MAX-VALUE(RESULT(s, a))
if sim-utility < worst
worst = sim-utility
return worst
MAX-VALUE(s)
If GAME-OVER(s)
return UTILITY(s)
For every a ∊ Actions(s)
sim-utility = MIN-VALUE(RESULT(s, a))
if sim-utility > best
best = sim-utility
return best
要在JavaScript中查看此算法的版本,请在此处查看: https : //github.com/AaronCCWong/portfolio/blob/master/src/util/tictactoe/ComputerPlayer.js#L15
MINIMAX显然是深度优先搜索的应用程序。 它的运行时间为O(b^n) ,其中b是给定回合中有效移动的最大次数, n是树的最大深度。
所有这些都假定我们正在与理性的对手对抗。 如果对手打得不够理想怎么办? 很难看出在这种情况下MINIMAX不会做得更好,因为对手的举动不会使我们进入可能的效用最小的状态。
精明的读者会意识到,这种算法不会创造出永远赢的AI。 但是,它确实创建了无与伦比的井字游戏计算机播放器。 也就是说,充其量您将能够打平。 如果像我一样,您的动作太快,甚至可能失败。
随时在tic-tac-toe中迷路: https : //www.aaronccwong.com/tic-tac-toe
免责声明:如果您声称自己击败了它,请不要害怕在下面的评论中列出您为赢得比赛所采取的行动。 每次计算机都会进行相同的移动,因此我们可以验证您确实是井字游戏的大师。 通过教我们如何击败它,您还将为人类提供优质的服务。
翻译自: https://hackernoon.com/i-created-an-ai-that-beats-me-at-tic-tac-toe-3ea6ba22cd71
井字棋游戏ai