基于混合策略的麻雀搜索算法
文章目录
- 一、理论基础
-
- 1、麻雀搜索算法
- 2、麻雀搜索算法的改进策略
-
- (1)改进的Circle混沌映射初始化种群
- (2)发现者位置更新策略的改进
- (3)加入者位置更新策略的改进
- (4)镜像选择
- (5)模拟退火机制
- 3、HSSA算法整体流程
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、麻雀搜索算法
请参考这里。
2、麻雀搜索算法的改进策略
(1)改进的Circle混沌映射初始化种群
混沌映射初始化种群可以有效改善初始解容易出现聚集、在解空间里覆盖率不高、个体之间差异性较低等问题。Circle映射比较稳定且混沌值的覆盖率较高,但Circle映射混沌值依旧分布不均匀,在 [ 0.2 , 0.6 ] [0.2,0.6] [0.2,0.6]之间的取值较为密集,所以将Circle映射公式稍作改进,使其混沌值分布更加均匀。
原Circle混沌映射表达式为: x n + 1 = mod ( x n + 0.2 − 0.5 2 π sin ( 2 π ⋅ x n ) , 1 ) (1) x_{n+1}=\text{mod}(x_n+0.2-\frac{0.5}{2\pi}\sin(2\pi\cdot x_n),1)\tag{1} xn+1=mod(xn+0.2−2π0.5sin(2π⋅xn),1)(1)改进之后的Circle混沌映射表达式为: x n + 1 = mod ( 3.85 x n + 0.4 − 0.7 3.85 π sin ( 3.85 π ⋅ x n ) , 1 ) (2) x_{n+1}=\text{mod}(3.85x_n+0.4-\frac{0.7}{3.85\pi}\sin(3.85\pi\cdot x_n),1)\tag{2} xn+1=mod(3.85xn+0.4−3.85π0.7sin(3.85π⋅xn),1)(2)其中, n n n为解的维度。为直观清晰地显示改进效果,取 n n n为2000。改进前后两者的初始解维度分布图和初始解维度分布直方图如下所示。
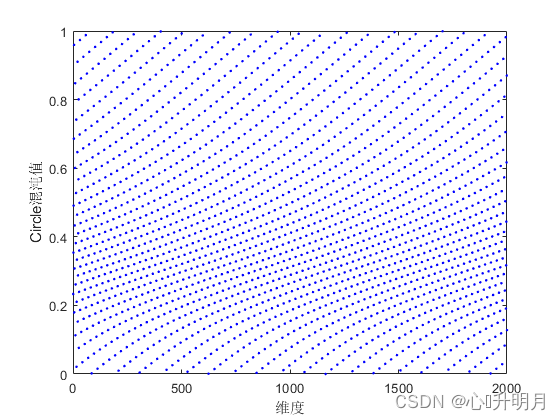
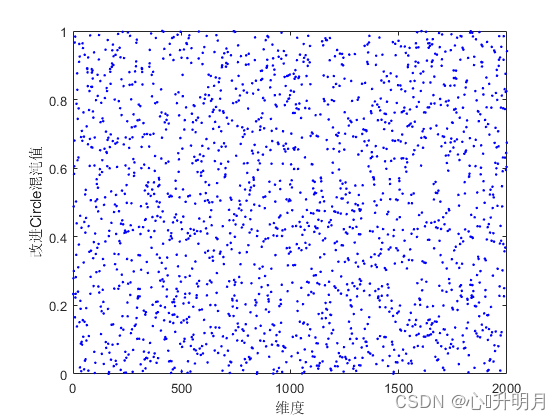


将图1和图2进行对比、图3和图4进行对比,可以发现改进的Circle映射混沌值分布更为均匀。因此采用改进的Circle映射初始化种群,增强种群的多样性,进而增强算法的寻优能力。
(2)发现者位置更新策略的改进
麻雀算法中发现者的位置更新公式如下: x i , j t + 1 = { x i , j t ⋅ exp ( − i α ⋅ i t e r max ) , R 2 < S T x i , j t + Q ⋅ L , R 2 ≥ S T (3) x_{i,j}^{t+1}=\begin{dcases}x_{i,j}^t\cdot\exp(-\frac{i}{\alpha\cdot iter_{\max}}),\quad R_2
当 R 2 < S T R_2
由于表达式 c 1 ( ( u b − l b ) c 2 + l b ) c_1((ub-lb)c_2+lb) c1((ub−lb)c2+lb)可以协调樽海鞘群的全局和局部搜索能力,提高算法前期搜索范围,所以将其应用于麻雀算法发现者的位置更新策略中。但直接加入麻雀算法会导致麻雀算法前期搜索范围过广,降低了麻雀算法的搜索精度和效率,所以对此表达式稍作修改,满足提高麻雀算法前期全局搜索能力和范围的要求。又因为 R 2 ≥ S T R_2\geq ST R2≥ST时,公式左右两侧代表个体在某维度的位置,为具体的数值,所以 L \boldsymbol L L应略去。最终发现者的位置更新表达式如下: x i , j t + 1 = { x i , j t ⋅ c 1 ( ( u b − l b ) c 2 + l b ) ( 1 + c 3 ) ⋅ u b , R 2 < S T x i , j t + Q , R 2 ≥ S T (6) x_{i,j}^{t+1}=\begin{dcases}x_{i,j}^t\cdot\frac{c_1((ub-lb)c_2+lb)}{(1+c_3)\cdot ub},\quad R_2
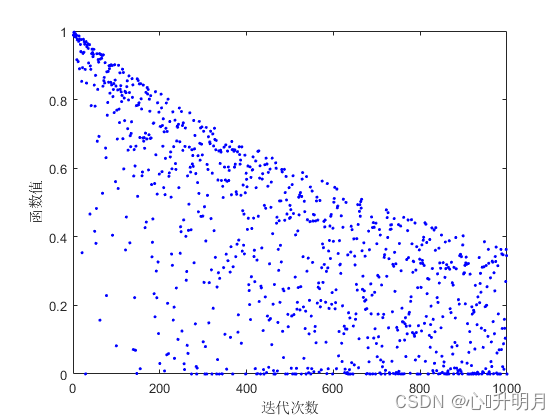
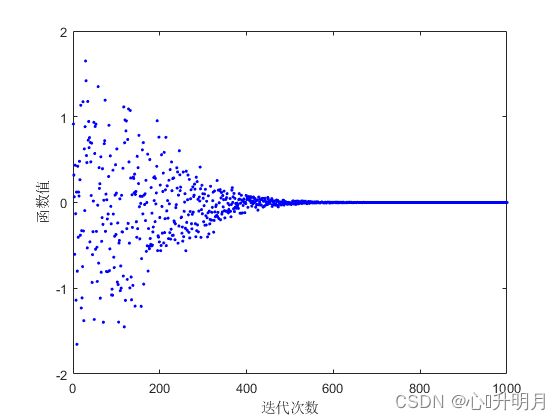
根据两个更新策略的仿真图可知,改进后的麻雀算法发现者在迭代前期不一定每维都在变小,增加了每维向正负方向变大的可能性,提高了麻雀种群的搜索范围和全局搜索能力。同时也兼顾了算法迭代后期的收敛速度和局部搜索能力。所以改进后的发现者位置更新策略有效地协调了算法的全局和局部的搜索能力。
(3)加入者位置更新策略的改进
加入者的位置更新公式如下: x i , j t + 1 = { Q ⋅ exp ( x w , j t − x i , j t i 2 ) , i > n / 2 x p , j t + 1 + 1 D ∑ j = 1 D ( r a n d { − 1 , 1 } ⋅ ∣ x i , j t − x p , j t + 1 ∣ ) , i ≤ n / 2 (7) x_{i,j}^{t+1}=\begin{dcases}Q\cdot\exp(\frac{x_{\text{w},j}^t-x_{i,j}^t}{i^2}),\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\, i>n/2\\[2ex]x_{\text p,j}^{t+1}+\frac 1D\sum_{j=1}^D(rand\{-1,1\}\cdot\left|x_{i,j}^t-x_{\text p,j}^{t+1}\right|),\quad i\leq n/2\end{dcases}\tag{7} xi,jt+1=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧Q⋅exp(i2xw,jt−xi,jt),i>n/2xp,jt+1+D1j=1∑D(rand{−1,1}⋅∣∣xi,jt−xp,jt+1∣∣),i≤n/2(7)其中, Q Q Q和 D D D同式(3)含义相同; x w , j t x_{\text{w},j}^t xw,jt是第 t t t次迭代后种群最差个体在第 j j j维的位置; x p , j t + 1 x_{\text p,j}^{t+1} xp,jt+1是第 t + 1 t+1 t+1次迭代时发现者最优个体在第 j j j维的位置。由加入者更新公式可知,加入者会以一定概率向发现者的最优位置靠近。但是加入者向发现者最优位置移动的距离随机。所以引进自适应步长因子,控制加入者和发现者各维度之间的距离。改进后加入者的位置更新表达式如下: x i , j t + 1 = { Q ⋅ exp ( x w , j t − x i , j t i 2 ) , i > n / 2 x p , j t + 1 + H i , j ⋅ 1 D ∑ j = 1 D ( r a n d { − 1 , 1 } ⋅ ∣ x i , j t − x p , j t + 1 ∣ ) , i ≤ n / 2 (8) x_{i,j}^{t+1}=\begin{dcases}Q\cdot\exp(\frac{x_{\text{w},j}^t-x_{i,j}^t}{i^2}),\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\, i>n/2\\[2ex]x_{\text p,j}^{t+1}+H_{i,j}\cdot\frac 1D\sum_{j=1}^D(rand\{-1,1\}\cdot\left|x_{i,j}^t-x_{\text p,j}^{t+1}\right|),\quad i\leq n/2\end{dcases}\tag{8} xi,jt+1=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧Q⋅exp(i2xw,jt−xi,jt),i>n/2xp,jt+1+Hi,j⋅D1j=1∑D(rand{−1,1}⋅∣∣xi,jt−xp,jt+1∣∣),i≤n/2(8) H i , j = s 1 + ( s 2 − s 1 ) ⋅ ∣ x i , j t − x p , j t + 1 ∣ / M j (9) H_{i,j}=s_1+(s_2-s_1)\cdot\left|x_{i,j}^t-x_{\text p,j}^{t+1}\right|/M_j\tag{9} Hi,j=s1+(s2−s1)⋅∣∣xi,jt−xp,jt+1∣∣/Mj(9)其中, H i , j H_{i,j} Hi,j为第 i i i个加入者在第 j j j维的步长因子; s 1 s_1 s1取0.001, s 2 s_2 s2取1; M j M_j Mj为当前加入者和发现者最优位置之间在第 j j j维的最大距离。
(4)镜像选择
镜像选择是基于反向学习的思想,对每次迭代后的种群进行变异操作。变异公式为: X i ′ = u + l − X i (10) X_i'=u+l-X_i\tag{10} Xi′=u+l−Xi(10)其中, X i X_i Xi是迭代后的第 i i i个个体; X i ′ X_i' Xi′是通过变异产生的镜像个体; u u u和 l l l分别表示个体取值的上下界。随后新生成的 N N N个镜像个体和原种群的 N N N个个体合并,根据适应度值排序,由优胜劣汰原则选出 N N N个较为优秀的个体进行最优位置更新,然后进行下次循环。该方法通过种群变异增加了种群多样性,通过对最优个体的选择,提升了每次迭代后个体的质量,提高了算法的寻优效率和收敛速度,同时也提高了算法的寻优精度。为此选取30个麻雀个体对式(11)进行一次迭代寻优实验,观察镜像选择前后的种群位置对比图。图中 x , y , z x,y,z x,y,z代表三维图坐标轴,上下界取值分别为100和-100,红色圆点表示30个种群个体,蓝色三角形表示全局最优位置,坐标为 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)。 f ( x ) = ∑ i = 1 n x i 2 (11) f(x)=\sum_{i=1}^nx_i^2\tag{11} f(x)=i=1∑nxi2(11)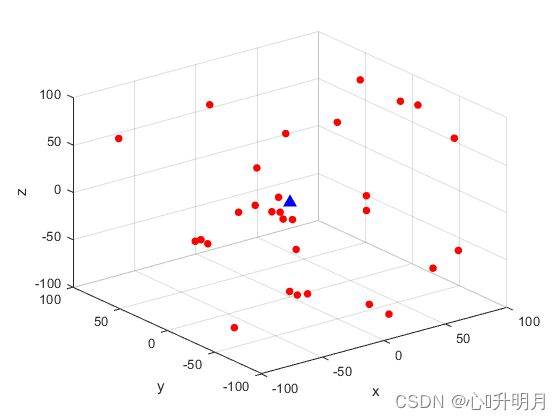
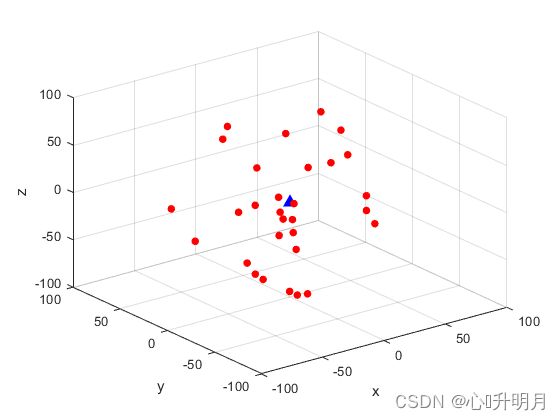
由镜像选择前后的种群位置图可知,镜像选择之后生成的新种群会较原种群的位置更加优秀,进而可以提高算法的寻优速度和寻优精度。变异后得到的新种群对于算法跳出局部最优也有一定的帮助。
(5)模拟退火机制
为了更加高效地提升麻雀算法跳出局部最优的能力,引进了模拟退火机制,来帮助麻雀算法跳出局部最优。即当新位置的适应度值大于当前全局最优位置的适应度值时,仍然有一定的概率接受该新位置。其中退火温度 T T T决定了麻雀种群接收新位置的概率, T T T越高,麻雀种群接收新位置的概率越高,反之则越低。退火温度 T T T随着迭代次数的增加而递减,退火温度 T T T的表达式为: T ( s + 1 ) = ε T ( s ) (12) T(s+1)=\varepsilon T(s)\tag{12} T(s+1)=εT(s)(12)其中, s s s表示迭代次数; ε \varepsilon ε表示退火系数,取值为 [ 0.9 , 1 ] [0.9,1] [0.9,1]。进行全局最优位置更新的时候,将新位置的适应度值 F n F_\text{n} Fn和原位置的适应度值 F o F_\text{o} Fo作差: Δ F = F n − F o (13) \Delta F=F_\text{n}-F_\text{o}\tag{13} ΔF=Fn−Fo(13)当 Δ F ≤ 0 \Delta F\leq0 ΔF≤0时,直接接受新位置;反之,根据以下公式进行判断: exp ( − Δ F T ) ≥ r a n d ( 0 , 1 ) (14) \exp(-\frac{\Delta F}{T})\geq rand(0,1)\tag{14} exp(−TΔF)≥rand(0,1)(14)如果此式成立,则接受新位置,反之不接受。
3、HSSA算法整体流程
步骤一 初始化参数,包括种群数量、发现者和警戒者的比例、警戒阈值和安全阈值等。
步骤二 利用改进的Circle混沌映射初始化种群。
步骤三 计算麻雀个体的适应度值,并对其排序,找出最优和最差适应度值的个体及其位置。
步骤四 根据式(6)进行发现者位置的更新。
步骤五 根据式(8)进行加入者位置的更新。
步骤六 根据原麻雀算法的警戒者更新公式进行警戒者的位置更新。
步骤七 对更新后的麻雀个体的位置进行镜像选择,选出适应度值较好的前 N N N个个体组成新的麻雀种群。
步骤八 将新种群的适应度值与原种群的适应度值进行比较,进行个体位置的更新。
步骤九 由模拟退火机制,进行全局最优位置的更新。
步骤十 判断是否达到迭代循环结束条件,若达到,则进行下一步,否则,跳转到步骤三。
步骤十一 算法执行结束,输出并记录最优结果。
二、仿真实验与结果分析
将HSSA与SSA、PSO、ABC和WOA进行对比,以文献[1]中表1的8个函数为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算50次,结果显示如下:
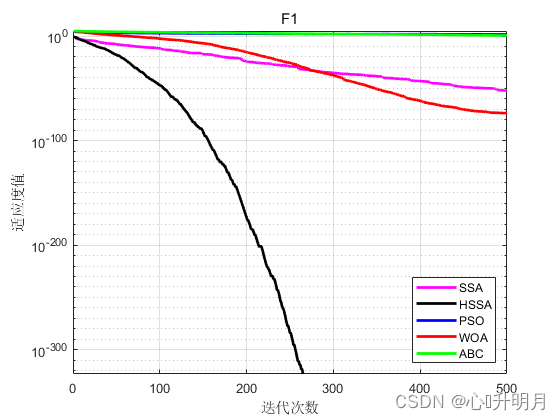
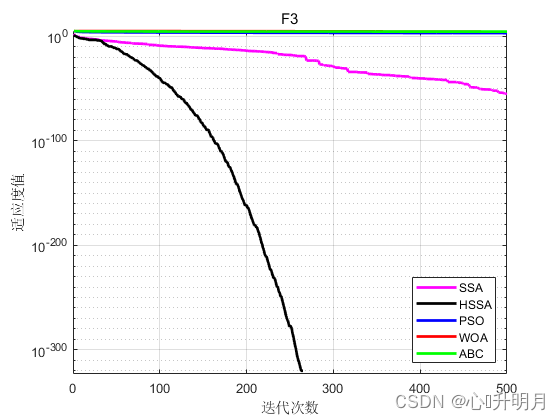
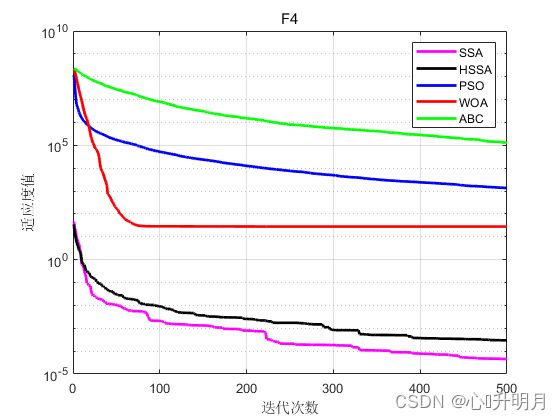

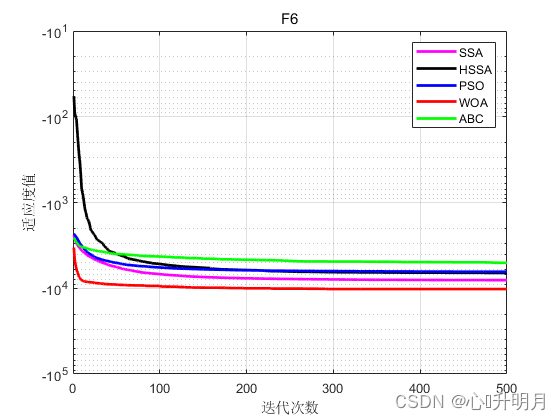
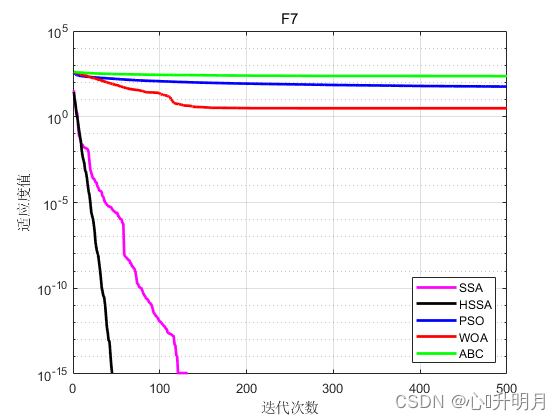

函数:F1
SSA:最差值: 2.0804e-51, 最优值: 0, 平均值: 4.1608e-53, 标准差: 2.9421e-52
HSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
PSO:最差值: 71.3909, 最优值: 13.3869, 平均值: 32.9022, 标准差: 12.4146
WOA:最差值: 5.6068e-73, 最优值: 2.3726e-85, 平均值: 1.5601e-74, 标准差: 8.1093e-74
ABC:最差值: 8.7913, 最优值: 1.0912, 平均值: 3.3055, 标准差: 1.5362
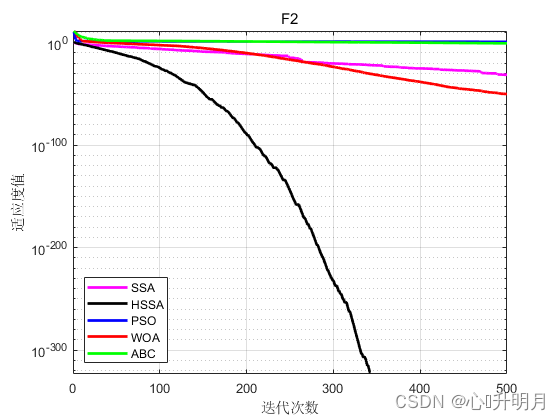
函数:F2
SSA:最差值: 1.9212e-30, 最优值: 0, 平均值: 3.8975e-32, 标准差: 2.7165e-31
HSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
PSO:最差值: 13.5615, 最优值: 2.739, 平均值: 5.8107, 标准差: 2.1361
WOA:最差值: 1.9958e-49, 最优值: 7.4621e-59, 平均值: 6.8201e-51, 标准差: 2.9632e-50
ABC:最差值: 0.29561, 最优值: 0.073898, 平均值: 0.17591, 标准差: 0.053137
函数:F3
SSA:最差值: 2.1293e-54, 最优值: 0, 平均值: 6.9566e-56, 标准差: 3.1846e-55
HSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
PSO:最差值: 2987.0971, 最优值: 442.286, 平均值: 1353.916, 标准差: 514.3413
WOA:最差值: 63772.5146, 最优值: 6187.4891, 平均值: 44497.635, 标准差: 13141.1421
ABC:最差值: 42115.1531, 最优值: 22766.489, 平均值: 34743.2085, 标准差: 4040.314
函数:F4
SSA:最差值: 0.00034153, 最优值: 2.7941e-11, 平均值: 4.507e-05, 标准差: 7.0556e-05
HSSA:最差值: 0.0017136, 最优值: 8.8409e-07, 平均值: 0.00029604, 标准差: 0.00046377
PSO:最差值: 6686.9409, 最优值: 300.0079, 平均值: 1368.7643, 标准差: 1073.3004
WOA:最差值: 28.7974, 最优值: 27.0969, 平均值: 28.0667, 标准差: 0.51892
ABC:最差值: 674159.8164, 最优值: 21490.7233, 平均值: 129799.498, 标准差: 115374.6406
函数:F5
SSA:最差值: 0.0066308, 最优值: 1.249e-05, 平均值: 0.00059576, 标准差: 0.00096288
HSSA:最差值: 0.0005076, 最优值: 1.6849e-06, 平均值: 0.00012376, 标准差: 0.00012362
PSO:最差值: 0.17041, 最优值: 0.027409, 平均值: 0.076564, 标准差: 0.03522
WOA:最差值: 0.019645, 最优值: 1.6458e-05, 平均值: 0.004, 标准差: 0.0047316
ABC:最差值: 0.41675, 最优值: 0.10136, 平均值: 0.22914, 标准差: 0.075512
函数:F6
SSA:最差值: -6400.53, 最优值: -9389.9281, 平均值: -8039.2644, 标准差: 624.8936
HSSA:最差值: -118.1917, 最优值: -12339.0411, 平均值: -6618.8129, 标准差: 3613.0051
PSO:最差值: -4866.4421, 最优值: -7818.0348, 平均值: -6422.0395, 标准差: 738.1199
WOA:最差值: -7317.3371, 最优值: -12569.4847, 平均值: -10225.6589, 标准差: 1774.3932
ABC:最差值: -4405.6481, 最优值: -5914.5106, 平均值: -5047.7974, 标准差: 311.0936
函数:F7
SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
HSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
PSO:最差值: 93.1877, 最优值: 31.965, 平均值: 57.3817, 标准差: 13.9557
WOA:最差值: 156.5541, 最优值: 0, 平均值: 3.1311, 标准差: 22.1401
ABC:最差值: 261.02, 最优值: 194.0248, 平均值: 232.7217, 标准差: 14.5232
函数:F8
SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
HSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
PSO:最差值: 1.7057, 最优值: 1.1463, 平均值: 1.333, 标准差: 0.13591
WOA:最差值: 0.20534, 最优值: 0, 平均值: 0.0041068, 标准差: 0.029039
ABC:最差值: 1.0749, 最优值: 0.84516, 平均值: 1.0055, 标准差: 0.045137
实验结果表明改进型麻雀算法HSSA的寻优精度和收敛速度相较SSA有较大提升,和其他智能优化算法相比同样优势明显。
三、参考文献
[1] 宋立钦, 陈文杰, 陈伟海, 等. 基于混合策略的麻雀搜索算法改进及应用[J/OL]. 北京航空航天大学学报: 1-16 [2022-05-31].