101道算法javaScript描述

小册介绍

数据结构与算法是计算机专业必修课，但是对于前端工程师来说，沉浸在业务代码之中很少会和算法直接打交道，甚于说根本不需要用到什么算法。那么我们为什么要学习算法，意义何在？不会算法活不是一样能干。把一件事情做到极致是非常必要的职业心态，这离不开数据结构和算法。另一方面，再说面试，这和在学生时代为什么要学数理化是一个道理，考试要考，你就要学。面试造火箭，工作拧螺丝，面试官通过问几道算法题了解你的编程和逻辑思维能力并不奇怪。

万丈高楼平地起，基础知识掌握多少，一定程度上决定了我们的技术能走多远。想要作出一点事情，基础一定要扎实，要苦练“内功”。对于一名工程师来说，所谓的“内功”无非就是大学里所学的那些基础课程，计算机网络、数据结构与算法等。

内容由浅入深大致可以分为 3 个部分：

• 基础篇

这部分的内容先从考评算法的复杂度开始介绍，再从比较基础的字符串、数组入手，最后是一些数学相关的题目。让大家先从简单的内容上手，练好基本功，不要一上来就被算法吓到。

• 进阶篇

剖析稍复杂的数据结构与算法，再加上经典题目的实战练习，帮助你更加深入理解算法的精髓、提升算法思维，开始修炼更高深的“内功”。

• 高级篇

本部分来介绍一些比较高级的算法，可以理解为高深的“心法”，虽然难学，但是学会了之后会发现很管用，走遍天下都不怕。

我们解题不能一知半解，每道题每一种解法，都写上了解题思路和详细的解题步骤。让读者在解题的过程当中，更好地训练思维，知道答案是怎么来的，能够举一反三。

本小册子选取大厂面试高频算法题共计 101 道，大多数题目至少两种 JavaScript 解法，并附有详细的思路和解题过程，来帮你夯实、强化算法知识。

你会收获到什么？

• 更好的逻辑思维能力

• 对数据结构更深的理解

• 能够写出更加牛逼的代码

• 一份体面的工作

适宜人群

• 想看看机会的同学

• 一直想学习算法，出于某些原因没认真学的同学

你需要准备什么

• JavaScript 语言基础

• 一台电脑一杯咖啡

• 一颗热爱学习的心

学习指南

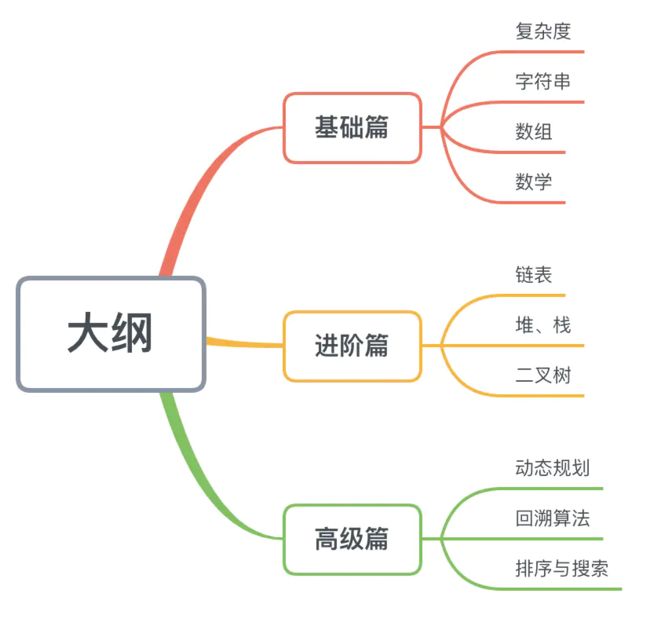
本小册子的内容可能比较多，为了能更好地帮助到大家，在阅读小册子的时候能够有更好的体验，在这里梳理整个小册子的目录结构。

小册子共分为 9 大章节：

也希望各位读者可以通过脑图可以对小册子的内容有更加明确的认识，提升阅读的收益。

如果觉得自己水平比较好的，完全可以跳着看，挑选能帮助你提高的内容来阅读。

高效地学习

大家都经历过高考，其实刷算法题就和刷高考题一样。举个例子，如果你的立体几何已经掌握得非常不错了，而导数是弱项，再去做 100 道立体几何还不如 10 道导数的题目进步的快。经常做自己熟悉的题目，进步并不是很大，投入产出比不高。算法也是如此，需要经常去做你不会的题目，同时一个题目挖掘更多更高效的解法。如果你发现学习的时候脑壳很痛，那么恭喜你，你真的在进步。

一起变得更好

如果在阅读过程发现有什么错误，欢迎留言，我们会第一时间回复，也希望你的留言可以帮助到其他的同学。

小册子的解题方法写得还是相对详细的，但是这个只是我们觉得。不要我们觉得，要大家觉得。毕竟每个人的基础不一样，大家在阅读过程当中如果有什么不明白的地方，想不明白的问题，欢迎在后台留言。

我们一直非常关注读者的阅读体验，如果觉得小册子的排版有哪里不够好，期待你提出宝贵的建议。

最后

数据结构和算法的学习是一个循序渐进的过程，如果可以仔细地阅读这本小册子，相信一定可以帮助到你。同时自己的思考和坚持很重要。好吧，说了那么多，还不赶快学习去。

开篇——复杂度

算法复杂度是考评算法执行效率和消耗资源的一个重要指标。在符合算法本身的要求的基础上，编写的程序运行时间越短，运行过程中占用的内存空间越少，意味着这个算法越“好”。

时间复杂度

时间复杂度是描述算法运行的时间。我们把算法需要运算的次数用输入大小为 nn 的函数来表示，计作 T(n)T(n)。时间复杂度通常用\mathcal{O}(n)O(n)来表示，公式为T(n) = \mathcal{O}(f(n))T(n)=O(f(n))，其中f(n)f(n)表示每行代码的执行次数之和，注意是执行次数。

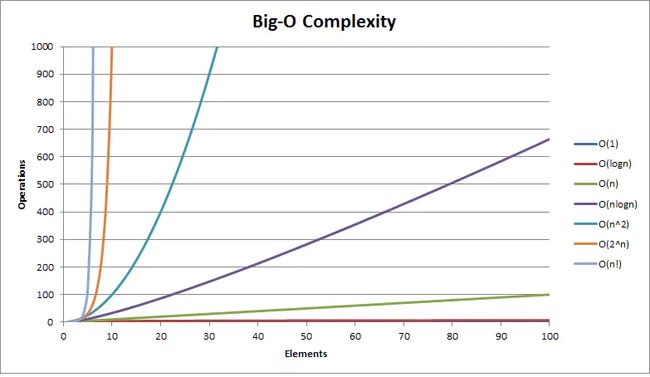
常见的时间复杂度

名称	运行时间T(n)T(n)T(n)	时间举例
常数	O(1)\mathcal{O}(1)O(1)	3	-
线性	\mathcal{O}(n)O(n)	nn	操作数组
平方	\mathcal{O}(n^2)O(n2)	n^2n2	冒泡排序
对数	\mathcal{O}(log(n))O(log(n))	log(n)log(n)log(n)	二分搜索

• \mathcal{O}(1)O(1) 复杂度

算法执行所需要的时间不随着某个变量nn的大小而变化，即此算法时间复杂度为一个常量，可表示为 \mathcal{O}(1)O(1)

直接上代码

const a = 1;
console.log(a);

const a = 1;
console.log(a, 1);
console.log(a, 2);
console.log(a, 2);

\mathcal{O}(1)O(1)表示常数级别的复杂度，不管你是\mathcal{O}(几)O(几)，统一给你计作 \mathcal{O}(1)O(1)

• \mathcal{O}(n)O(n) 复杂度

for (let i = 0; i < n; i++) {
    // do something
}

上面这段代码，写了一个 for 循环，从 0 到 nn，不管 nn 是多少，都要循环 nn 次，而且只循环 nn 次，所以得到复杂度为 \mathcal{O}(n)O(n)

• \mathcal{O}(n^2)O(n2) 复杂度

for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; i++) {
        // do something
    }
}

上面的程序嵌套了两个循环，外层是 0 到 nn，内层基于每一个不同的 ii，也要从 0 到 nn 执行，得到复杂度为 \mathcal{O}(n^2)O(n2)。可以看出，随着 nn 增大，复杂度会成平方级别增加。

• \mathcal{O}(log (n))O(log(n)) 对数复杂度

  for (let i = 1; i <= n; i *= 2) {
      // do something
  }
  

讲到这里顺便来复习一下高中数学知识，函数y = log_a{x}y=logax叫做对数函数，aa就是对数函数的底数。

对数复杂度是比较常见的一种复杂度，也是比较难分析的一种复杂度。观察上面的代码，ii 从 1 开始，每循环一次就乘以 2，直到 ii 大于 nn 时结束循环。

2 ^1 --> 2^2 --> 2^3 … -->2^x21−−>22−−>23…−−>2x

观察上面列出 i 的取值发现，是一个等比数列，要知道循环了多少次，求出 xx 的值即可。由 2^x = n2x=n得到，x = log_2{n}x=log2n，所以这段代码的时间复杂度为log_2{n}log2n。

如果把上面的 i *= 2 改为 i *= 3，那么这段代码的时间复杂度就是 log_3{n}log3n。

根据换底公式：

log_c{a} * log_a{b} = log_c{b}logca∗logab=logcb

因此 log_3{n} = log_3{2} * log_2{n}log3n=log32∗log2n ，而 log_3{2}log32 是一个常量，得到 \mathcal{O}(log_3(n)) = \mathcal{O}(log_2(n))O(log3(n))=O(log2(n))。所以，在对数时间复杂度的表示中，我们忽略对数的“底”，我不管你底数是多少，统一计作\mathcal{O}(log (n))O(log(n))。

递归的时间复杂度

在面试的时候，可能会写到一些递归的程序，那么递归的时间复杂度如何考虑？

递归算法中，每个递归函数的的时间复杂度为O(s)O(s)，递归的调用次数为 nn，则该递归算法的时间复杂度为 O(n) = n * O(s)O(n)=n∗O(s)

我们先来看一个经典的问题，斐波那契数列(Fibonacci sequence)：

F(0)=1，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2,n ∈ N*）F(0)=1，F(1)=1,F(n)=F(n−1)+F(n−2)（n≥2,n∈N∗）

function fibonacci(n) {
    if (n === 0 || n === 1) {
        return 1;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

我们很容易写出上面这样一段递归的代码，往往会忽略了时间复杂度是多少，换句话说调用多少次。可以代一个数进去，例如 n = 5，完了之后大概就能理解递归的时间复杂度是怎么来的。

上图把 n = 5 的情况都列举出来。可以看出，虽然代码非常简单，在实际运算的时候会有大量的重复计算。

在 nn 层的完全二叉树中，节点的总数为 2^n -12n−1，所以得到 F(n)F(n) 中递归数目的上限为 2^n -12n−1。因此我们可以毛估出 F(n)F(n) 的时间复杂度为 {\mathcal{O}(2^n)}O(2n)。

时间复杂度为 \mathcal{O}(2^n)O(2n)，指数级的时间复杂度，显然不是最优的解法，让计算机傻算了很多次，所以在面试时要稍微留意，如果写出这样的代码，可能会让你的面试官不太满意。

空间复杂度

空间复杂度是对算法运行过程中临时占用空间大小的度量，一个算法所需的存储空间用f(n)f(n)表示，可得出S(n)=\mathcal{O}(f(n))S(n)=O(f(n))，其中 nn 为问题的规模，S(n)S(n)表示空间复杂度。通常用 S(n)S(n) 来定义。

常见的空间复杂度

• {\mathcal{O}(1)}O(1) 复杂度

算法执行所需要的临时空间不随着某个变量 nn 的大小而变化，即此算法空间复杂度为一个常量，可表示为 {\mathcal{O}(1)}O(1)

const a = 1;
const b = 2;
console.log(a);
console.log(b);

以上代码，分配的空间不会随着处理数据量的变化而变化，因此得到空间复杂度为{\mathcal{O}(1)}O(1)

• {\mathcal{O}(n)}O(n) 复杂度

先来看这样一段代码

const arr = new Array(n);
for (let i = 0; i < n; i++) {
    // do something
}

上面这段代码的第一行，申请了长度为 nn 的数组空间，下面的 for 循环中没有分配新的空间，可以得出这段代码的时间复杂度为 {\mathcal{O}(n)}O(n)。

对数阶的空间复杂度非常少见，而且空间复杂度的分析相对与时间复杂度分析简单很多，这部分不再阐述。

时间空间相互转换

对于一个算法来说，它的时间复杂度和空间复杂度往往是相互影响的。

那我们熟悉的 Chrome 来说，流畅性方面比其他厂商好了多人，但是占用的内存空间略大。

当追求一个较好的时间复杂度时，可能需要消耗更多的储存空间。 反之，如果追求较好的空间复杂度，算法执行的时间可能就会变长。

总结

常见的复杂度不多，从低到高排列就这么几个：O(1)O(1)、{O(log(n))}O(log(n))、{O(n)}O(n)、{O(n^2)}O(n2)，等学完后面的章节你会发现，复杂度基本上逃不走，都是上面这个几个。

字符串

在计算机中，字符串是由零个或多个字符组成的有限序列。字符串也是 JavaScript 中最基本的数据类型，学习字符串也是学习编程的基础。

说到字符串，我相信你肯定很熟悉了，是不是觉得很简单。接下来看题。

本章节分为 3 个部分：

• Part 1
  • 翻转数组
  • 有效的字母异位词
  • 字符串翻转整数
• Part 2
  • 报数
  • 反转字符串
  • 字符串中的第一个唯一字符
• Part 3
  • 验证回文字符串
  • 实现 strStr()
  • 最长公共前缀
  • 最长回文子串

阅读完本章节，你将有以下收获：

• 熟悉 JavaScript 中的基本操作
• 能够熟练解决字符串一些较基础的问题

翻转整数、有效的字母异位词和翻转整数

翻转整数

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

示例

示例 1:
输入: 123
输出: 321

示例 2:
输入: -123
输出: -321

示例 3:
输入: 120
输出: 21

注意:

假设我们的环境只能存储得下 32 位的有符号整数，则其数值范围为 [−231,231−1][−2^{31}, 2^{31} − 1][−231,231−1]。请根据这个假设，如果反转后整数溢出那么就返回 0。

方法一 翻转字符串方法

思路

如果将数字看成是有符号位的字符串，那么我们就能够通过使用 JS 提供的字符串方法来实现非符号部分的翻转，又因为整数的翻转并不影响符号，所以我们最后补充符号，完成算法。

详解

1. 首先设置边界极值；
2. 使用字符串的翻转函数进行主逻辑；
3. 补充符号
4. 然后拼接最终结果

代码

/**
 * @param {number} x
 * @return {number}
 */
const reverse = (x) => {
  // 非空判断
  if (typeof x !== 'number') {
    return;
  }
  // 极值
  const MAX = 2147483647;
  const MIN = -2147483648;

  // 识别数字剩余部分并翻转
  const rest =
    x > 0
      ? String(x)
        .split('')
        .reverse()
        .join('')
      : String(x)
        .slice(1)
        .split('')
        .reverse()
        .join('');

  // 转换为正常值，区分正负数
  const result = x > 0 ? parseInt(rest, 10) : 0 - parseInt(rest, 10);

  // 边界情况
  if (result >= MIN && result <= MAX) {
    return result;
  }
  return 0;
};

复杂度分析

• 时间复杂度：O(n)O(n)O(n)

  代码中 reverse 函数时间复杂度为 O(n)O(n)O(n)，nnn 为整数长度，因此时间复杂度为 O(n)O(n)O(n)，考虑到32位整数最大长度为 11，即 -2147483648，也可认为是常数时间复杂度 O(1)O(1)O(1)。

• 空间复杂度：O(n)O(n)O(n)

  代码中创建临时 String 对象，nnn 为整数长度，因此空间复杂度为 O(n)O(n)O(n)，考虑到32位整数最大长度为11，即-2147483648，因此空间复杂度为 O(1)O(1)O(1)。

方法二 类似 欧几里得算法 求解

思路

我们借鉴欧几里得求最大公约数的方法来解题。符号的处理逻辑同方法一，这里我们通过模 10 取到最低位，然后又通过乘 10 将最低位迭代到最高位，完成翻转。

详解

1. 设置边界极值；
2. 取给定数值的绝对值，遍历循环生成每一位数字，借鉴欧几里得算法，从 num 的最后一位开始取值拼成新的数
3. 同步剔除掉被消费的部分
4. 如果最终结果为异常值，则直接返回 0；如果原本数据为负数，则对最终结果取反
5. 返回最终结果

代码

/**
 * @param {number} x
 * @return {number}
 */
const reverse = (x) => {
  // 获取相应数的绝对值
  let int = Math.abs(x);
  // 极值
  const MAX = 2147483647;
  const MIN = -2147483648;
  let num = 0;

  // 遍历循环生成每一位数字
  while (int !== 0) {
    // 借鉴欧几里得算法，从 num 的最后一位开始取值拼成新的数
    num = (int % 10) + (num * 10);
    // 剔除掉被消费的部分
    int = Math.floor(int / 10);
  }
  // 异常值
  if (num >= MAX || num <= MIN) {
    return 0;
  }
  if (x < 0) {
    return num * -1;
  }
  return num;
};

复杂度分析：

• 时间复杂度：O(n)O(n)O(n)

  代码中使用 for 循环，次数为 nnn，即整数的长度，因此时间复杂度为 O(n)O(n)O(n)。

• 空间复杂度：O(1)O(1)O(1)

  算法中只用到常数个变量，因此空间复杂度为 O(1)O(1)O(1)。

有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例1

输入: s = "anagram", t = "nagaram"
输出: true

示例2

输入: s = "rat", t = "car"
输出: false

方法一 利用数组sort()方法

思路

首先，对字符串字母进行排序，然后，比较两字符串是否相等。

详解

1. 首先，将字符串转为数组。
2. 利用数组 sort 方法进行排序。
3. 然后，转为字符串进行比较，如果相等返回 true，反之返回 false。

代码

const isAnagram = (s, t) => {
  const sArr = s.split('');
  const tArr = t.split('');
  const sortFn = (a, b) => {
    return a.charCodeAt() - b.charCodeAt();
  };
  sArr.sort(sortFn);
  tArr.sort(sortFn);
  return sArr.join('') === tArr.join('');
};

复杂度分析

• 时间复杂度：O(nlogn)O(nlogn)O(nlogn)

  JavaScript 的 sort 方法的实现原理，当数组长度小于等于 10 的时候，采用插入排序，大于 10 的时候，采用快排，快排的平均时间复杂度是 O(nlogn)O(nlogn)O(nlogn)。

• 空间复杂度：O(n)O(n)O(n) 算法中申请了 2 个数组变量用于存放字符串分割后的字符串数组，所以数组空间长度跟字符串长度线性相关，所以为 O(n)O(n)O(n)。

方法二 计数累加方法

思路

声明一个对象记录字符串每个字母的个数，另外一个字符串每项与得到的对象做匹配，最后，根据计数判断是否相等。

详解

1. 首先，声明一个变量，遍历其中一个字符串 s 或 t，对每个字母出现的次数进行累加。
2. 然后，遍历另一个字符串，使每一个字母在已得到的对象中做匹配，如果匹配则对象下的字母个数减 1，如果匹配不到，则返回 false，如果最后对象中每个字母个数都为 0，则表示两字符串相等。

代码

const isAnagram = (s, t) => {
  if (s.length !== t.length) {
    return false;
  }
  const hash = {};
  for (const k of s) {
    hash[k] = hash[k] || 0;
    hash[k] += 1;
  }
  for (const k of t) {
    if (!hash[k]) {
      return false;
    }
    hash[k] -= 1;
  }
  return true;
};

复杂度分析

• 时间复杂度：O(n)O(n)O(n)

  算法中使用了 2 个单层循环，因此，时间复杂度为 O(n)O(n)O(n)。

• 空间复杂度：O(1)O(1)O(1)

  申请的变量 hash 最大长度为 256，因为 Ascii 字符最多 256 种可能，因此，考虑为常量空间，即 O(1)O(1)O(1)。