回溯算法理论及应用

一. 回溯算法基础理论

算法思想：在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根节点出发深度搜索解空间树。当搜索到某一节点时，要先判断该节点是否包含问题的解，如果包含就从该节点出发继续深度搜索下去，否则逐层向上回溯。一般在搜索过程中都会添加相应的剪枝函数，避免无效解的搜索，提高算法效率。

解空间：解空间就是所有解的可能取值构成的空间，一个解往往包含了得到这个解的每一步，往往就是对应解空间树中一条从根节点到叶子节点的路径。子集树和排列树都是一种解空间，他们不是真实存在的数据结构，也就是说并不是真的有这样一棵树，只是抽象出的解空间树。

二. 子集树

1. 输出所有的子集

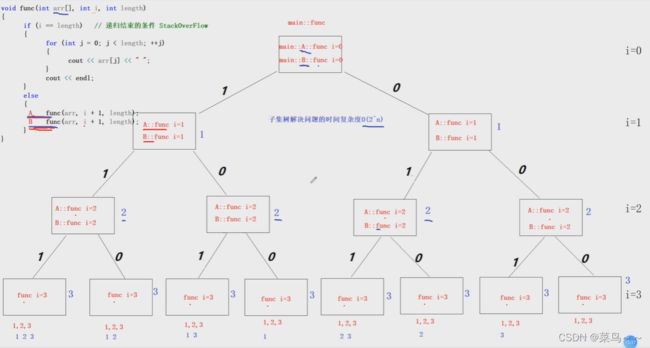
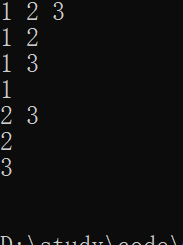
输出{1,2,3}中所有的子集

void fun(int arr[], int i, int length,int x[])
{
	if (i == length)
	{
		for (int j = 0; j < length; j++)
		{
			if (x[j] == 1)
			{
				cout << arr[j] << " ";
			}
		}
		cout << endl;
	}
	else
	{
		x[i] = 1;
		fun(arr, i + 1, length, x);
		x[i] = 0;
		fun(arr, i + 1, length, x);
	}
}
int main()
{
	int arr[] = { 1,2,3 };
	int x[3]={0};
	int length = sizeof(arr) / sizeof(arr[0]);
	fun(arr, 0, length, x);
}

2. 整数选择问题求解

给定一组整数，从里面挑选一组整数，让选择的整数和和剩下的整数的和的差最小。

#include
#include
#include
using namespace std;

int arr[] = { 12,6,7,11,16,3,8 };
const int length = sizeof(arr) / sizeof(arr[0]);

//int x[length] = { 0 };//子集树辅助数组，记录节点走左孩子还是右孩子，1代表i节点被选择而0未被选择
//int bestx[length] = { 0 };//记录最优解
vector<int> x;
vector<int> bestx;

unsigned int minn = 0xFFFFFFFF;//记录最小的差值
int sum = 0;//记录所选子集数字总和
int r = 0;//记录未选择数字的和

//生成子集树
void fun(int i)
{
	//访问到子集树的一个叶子节点
	if (i == length)
	{
		int result = abs(sum - r);
		if (result < minn)
		{
			minn = result;
			//记录差值最小的子集
			/*
			for (int j = 0; j < length; j++)
			{
				bestx[j] = x[j];
			}
			*/
			bestx = x;
		}
	}
	else
	{
		//x[i] = 1;
		x.push_back(arr[i]);
		r -= arr[i];
		sum += arr[i];
		fun(i + 1);//选择i节点
		r += arr[i];
		sum -= arr[i];

		//x[i] = 0;
		x.pop_back();
		fun(i + 1);//不选择i节点
	}
}
int main()
{
	for (int n : arr)
	{
		r += n;
	}
	fun(0);
	/*
	for (int i = 0; i < length; i++)
	{
		if (bestx[i] == 1)
			cout << arr[i] << " ";
	}
	*/
	for (int a : bestx)
	{
		cout << a << " ";
	}
	cout << endl << minn << endl;
}

3. 2N整数选择问题

#include
#include
#include
using namespace std;

int arr[] = { 12,6,7,11,16,3,8 ,9 };
const int length = sizeof(arr) / sizeof(arr[0]);
vector<int> x;
vector<int> bestx;
unsigned int minn = 0xFFFFFFFF;
int sum = 0;
int r = 0;
int leftt = length;//记录未处理的数字个数
int cnt = 0;//记录遍历子集的个数，用于测试

void fun(int i)
{
	if (i == length)
	{
		cnt++;
		if (x.size() != length / 2)
			return;
		int result = abs(sum - r);
		if (result < minn)
		{
			minn = result;
			bestx = x;
		}
	}
	else
	{
		leftt--;//表示处理i节点，表示剩余的未处理元素的个数
		//剪左枝，提高算法效率，选择数字的前提：还未选择够n个数
		if (x.size() < length / 2)
		{
			x.push_back(arr[i]);
			r -= arr[i];
			sum += arr[i];
			fun(i + 1);
			r += arr[i];
			sum -= arr[i];
			x.pop_back();
		}
		//已选择的元素+未来能选择的元素如果小于n就不用向右子树继续遍历了
		//已选择树枝的个数+未来能选择数字的个数>=n个元素
		if (x.size() + leftt >= length / 2)
		{
			fun(i + 1);
		}
		//当前i节点已处理完成，回溯到其父节点
		leftt++;
	}
}
int main()
{
	for (int n : arr)
	{
		r += n;
	}
	fun(0);
	for (int n : bestx)

	{
		cout << n << " ";
	}
	cout << endl << "min:" << minn << endl;
	cout<<"遍历子集个数:" << cnt << endl;
}

如果没有剪枝操作，需要遍历256个子集，然而进行剪枝操作，只需要遍历70个子集就可以实现。

4. 挑数字问题

有一组没有重复数字的整数，请挑选出一组数字，让他们的值等于指定的值，不允许选择重复元素，存在打印解空间，不存在也打印。

(1) 使用子集树解决

int arr[] = {4,8,12,16,7,9,3};
int number = 18;
vector<int> x;//记录选择的数字
int sum = 0;//已选择的元素和
int r = 0;//未被处理的元素和  不要混淆未处理和未选择
int length = sizeof(arr) / sizeof(arr[0]);

void fun(int i)
{
	if (i == length)
	{
		if (sum != number)
			return;
		for (int v : x)
		{
			cout << v << " ";
		}
		cout << endl;
	}
	else
	{
		r -= arr[i];
		if (sum + arr[i] <= number)//剪左枝
		{
			sum += arr[i];
			x.push_back(arr[i]);
			fun(i + 1);
			sum -= arr[i];
			x.pop_back();
		}
		if (sum + r >= number)//剪右枝
		{
			fun(i + 1);
		}
		r += arr[i];
	}
}
int main()
{
	for (int v : arr)
	{
		r += v;
	}
	fun(0);
}

(2) 使用枚举法解决

枚举法可以解决的子集树一定可以解决，而子集树能解决的枚举法不一定能解决。

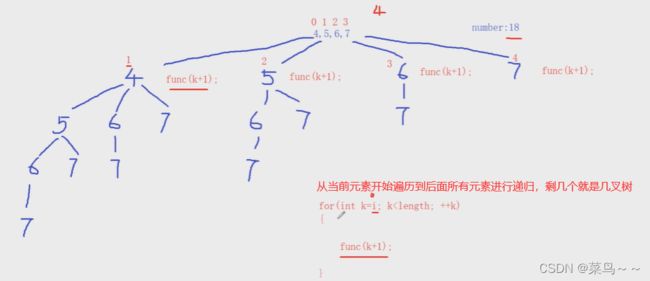
int arr[] = {4,8,12,16,7,9,3};
int number = 18;
vector<int> x;//存放选择的数字
int length = sizeof(arr) / sizeof(arr[0]);

void func(int i, int number)
{
	if (number == 0)
	{
		for (int v : x)
		{
			cout << v << " ";
		}
		cout << endl;
	}
	else
	{
		//从当前节点开始，把剩余元素的孩子节点生成
		for (int k = i; k < length; k++)
		{
			if (number >= arr[k])//剩余的元素小于number(待生成的元素值)
			{
				x.push_back(arr[k]);
				func(k + 1, number - arr[k]);//遍历孩子节点，arr[k]的孩子节点
				x.pop_back();
			}
		}
	}
}
int main()
{
	func(0, number);
}

允许重复选择元素

for (int k = i; k < length; k++)
		{
			if (number >= arr[k])
			{
				x.push_back(arr[k]);
				func(k,number-arr[k]);
				x.pop_back();
			}
		}

若这一组整数有重复数字，要求所选择的一组数字让他们的值等于指定的值，且不允许有重复元素。

先将这组整数排序再替换如下代码

for (int k = i; k < length; k++)
		{
			if (number >= arr[k]&&arr[k]!=arr[k+1])
			{
				x.push_back(arr[k]);
				func(k + 1, number - arr[k]);
				x.pop_back();
			}
		}

三. 排列数

1. 0-1背包问题

有一组物品，其重量分别为w1,w2…wn，其价值分别为v1,v2…vn，现在有一个背包，其容量为C，则怎么把物品装入背包，能够使背包的价值最大化？

#include
#include
using namespace std;

int w[] = { 12,5,8,9,6 };//物品重量
int v[] = { 9,11,4,7,8 };//物品价值
int c = 20;//背包容量
int cw = 0;//已选择物品的重量
int cv = 0;//已选择物品的价值
const int length = sizeof(w) / sizeof(w[0]);
vector<int> x;//选择的物品
vector<int> bestx;//记录最优选择的物品
int bestv = 0;//记录装入背包的最大价值
int r = 0;//未处理物品的总价值

void func(int i)
{
	if (i == length)
	{
		if (cv > bestv)
		{
			bestv = cv;
			bestx = x;
		}
	}
	else
	{
		r -= v[i];
		if (cw + w[i] <= c)
		{
			cv += v[i];
			cw += w[i];
			x.push_back(w[i]);
			func(i + 1);
			cv -= v[i];
			cw -= w[i];
			x.pop_back();
		}
		if (cv + r > bestv)
		{
			func(i + 1);
		}
		r += v[i];
	}
}
int main()
{
	for (int n : v)
	{
		r += n;
	}
	func(0);
	for (int n : bestx)
	{
		cout << n << " ";
	}
	cout << endl << bestv << endl;
}

2. 排列树理论及代码实现

排列数：原始序列不同的排列方式

#include
using namespace std;

void swap(int arr[], int k, int i)
{
	int tmp = arr[k];
	arr[k] = arr[i];
	arr[i] = tmp;
}
void func(int arr[], int i, int length)
{
	if (i == length)
	{
		for (int j = 0; j < length; j++)
		{
			cout << arr[j] << " ";
		}
		cout << endl;
	}
	else
	{
		//生成i节点的所有孩子节点
		for (int k = i; k < length; k++)
		{
			swap(arr,k, i);
			func(arr, i + 1, length);
			swap(arr,k, i);
		}
	}
}
int main()
{
	int arr[] = { 1,2,3,4 };
	func(arr, 0, sizeof(arr) / sizeof(arr[0]));
	return 0;
}

3. 八皇后问题求解

在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法

#include
using namespace std;

int cnt = 0;//统计8皇后的排列次数
void swap(int arr[], int i, int k)
{
	int tmp = arr[i];
	arr[i] = arr[k];
	arr[k] = tmp;
}
bool judge(int arr[], int i)//i表示当前要放置皇后棋子的位置
{
	for (int j = 0; j < i; j++)
	{
		if (i == j || arr[i] == arr[j] || abs(i - j) == abs(arr[i] - arr[j]))
		{
			return false;
		}
	}
	return true;
}
void func(int arr[],int i,int length)
{
	if (i == length)
	{
		cnt++;
		for (int j = 0; j < length; j++)
		{
			cout << arr[j] << " ";
		}
		cout << endl;
	}
	else
	{
		for (int k = i; k < length; k++)
		{
			swap(arr, i, k);
			//判断第i个位置的元素是否满足8皇后的条件
			if(judge(arr,i))
				func(arr, i + 1, length);//生成孩子节点，也就是说会生成一系列的排列方式
			swap(arr, i, k);
		}
	}
}
int main()
{
	//把arr数组的下标当作行，下标对应的元素当作列
	int arr[] = { 1,2,3,4,5,6,7,8 };
	func(arr, 0, sizeof(arr) / sizeof(arr[0]));
	cout << "总共有"<<cnt<<"种排列方法" << endl;
	return 0;
}

4. 基于穷举法的全排列实现

另一种实现全排列的代码满足leetcode刷题测试用例

#include
#include
using namespace std;


int arr[] = { 1,2,3 };
const int length = sizeof(arr) / sizeof(arr[0]);
vector<int> vec;
bool state[length];//记录所有元素是否被选择的状态
void func(int i)
{
	if (i == length)
	{
		for (int v : vec)
		{
			cout << v << " ";
		}
		cout << endl;
	}
	else
	{
		for (int k = 0; k < length; k++)
		{
			if (!state[k])
			{
				state[k] = true;
				vec.push_back(arr[k]);
				func(i + 1);//k表示的是可选择元素的起始下标；i表示层数
				state[k] = false;
				vec.pop_back();
			}
		}
	}
}
int main()
{
	func(0);
}