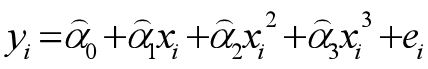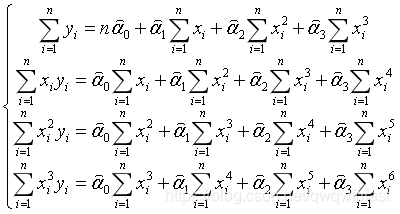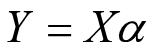【PYTHON】使用最小二乘法与梯度下降法求解多项式回归模型

多项式回归

对于一个足够光滑的函数，由泰勒公式可知，我们可以用一个多项式对该函数进行逼近，而且随着多项式阶数的提高，拟合的效果会越来越好。
多项式回归通常可写成下面的形式：

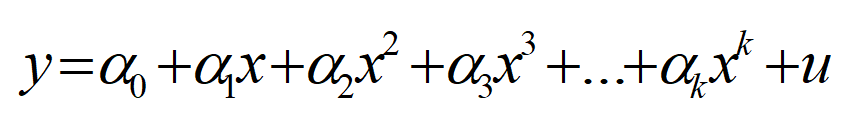
其中u表示随机干扰项，α0~αk是待定参数。

我们以下面模型为例，通过python编程实现最小二乘与梯度下降两种算法，并对结果进行可视化以更好地对它们进行比较。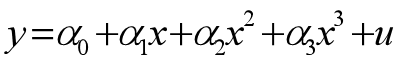

最小二乘法

假设有输入数据

那么有

其中ei表示残差。最小二乘法的原则是选择合适的参数使得全部观察值的残差平方和最小，用数学语言描述就是：

由数学的微积分知识可知，函数的极值在其一阶导数等于零的点取得。于是可令

整理得

写成矩阵形式为

简写成

其中

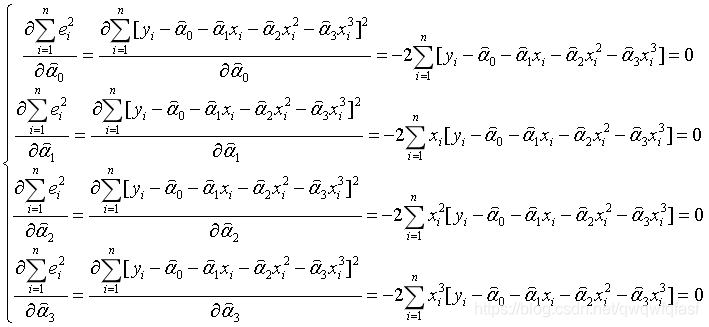
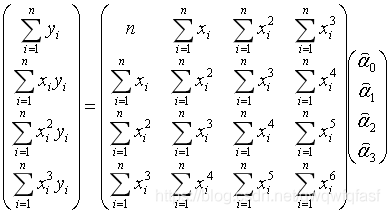
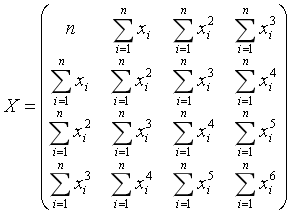
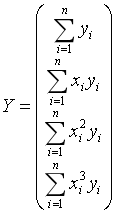
那么可得参数向量的解为

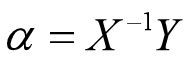
逆矩阵的计算可以用线性代数中的高斯消元法，这里不作展开。

梯度下降法

记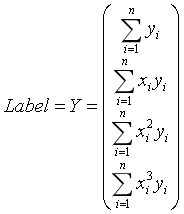
初始化一个噪声向量作为待训练的参数向量（通常从正态分布中取样）。

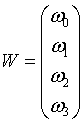
记

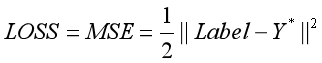
其中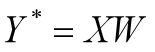
使用反向传播算法（基于链式法则）对参数向量求偏导，得

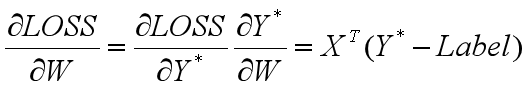
得到参数的梯度后，可利用梯度下降法对参数进行更新：

其中，Learning_Rate是一个实数，表示参数更新的幅度，不同的学习率会影响收敛的速度以及收敛的效果，比如有时学习率过大，会导致梯度爆炸，参数更新到inf，或者学习率过小，参数无法更新等等，需要耐心的调参以达到最好的训练效果。

编程实现及效果展示

利用基于python的numpy库，我们可以轻松实现数据集的创建，矩阵方程的求解，同时利用numpy的广播机制，可以很方便地处理哈达玛乘积等张量的运算操作。
同时要注意，利用梯度下降法进行求解时，如果创建的输入数据的数值比较大（比如几百或者几千）的时候，算法很容易产生梯度爆炸，这时候要对输入数据进行归一化再去训练参数向量，最后训练完成时，还要将参数向量乘以一个补偿因子来抵消对输入数据归一化产生的影响，具体的补偿因子取决于你的归一化技巧。
接着，利用python优秀的绘图库matplotlib，我们可以很容易地对训练过程中记录的损失值进行可视化，同时也可以可视化两种算法得到的结果以进一步作比较。
代码如下：

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['font.sans-serif']=['SimHei']#显示中文
plt.rcParams['axes.unicode_minus']=False#显示负号

#创建数据
n  = 60
xs = np.linspace(0,n,n)
ys = 0.2*xs**(5/2) - 0.8*xs**(1/2)

X = np.array([
    [n ,             np.sum(xs) ,    np.sum(xs**2) , np.sum(xs**3)],
    [np.sum(xs),     np.sum(xs**2) , np.sum(xs**3) , np.sum(xs**4)],
    [np.sum(xs**2) , np.sum(xs**3) , np.sum(xs**4) , np.sum(xs**5)],
    [np.sum(xs**3) , np.sum(xs**4) , np.sum(xs**5) , np.sum(xs**6)]
    ])

Y = np.array(
    [np.sum(ys) , np.sum(xs*ys) , np.sum(xs**2*ys) , np.sum(xs**3*ys)]
    ).reshape(4,1)

#基于最小二乘法
w_hat   = np.linalg.solve(X,Y)  #求解矩阵方程
y_hat_1 = w_hat[0] + w_hat[1]*xs + w_hat[2]*xs**2 + w_hat[3]*xs**3

#基于反向传播和梯度下降法
#归一化输入，否则输入太大，容易导致梯度爆炸
X_ = X/X.max()
Y_ = Y/Y.max()
lr = 0.01
steps = 3000
losses = []
W = 0.1*np.random.normal(size=(4,1),scale=1,loc=0)
W_copy = W.copy()
for step in range(steps):
    W -= lr*(X_.T)@(X_@W - Y_)
    loss = (np.sum((Y_ - X_@W)**2))/2
    losses.append(loss)
    print('Loss = ',loss)
#补偿归一化
make_up = Y.max()/X.max()
W = W*make_up 
y_hat_2 = W[0] + W[1]*xs + W[2]*xs**2 + W[3]*xs**3

#绘图比较
plt.subplot(1,2,1)
plt.scatter(xs,ys,c='b')
plt.plot(xs,y_hat_1,c='r')
plt.title('最小二乘法')

plt.subplot(1,2,2)
plt.scatter(xs,ys,c='b')
plt.plot(xs,y_hat_2,c='r')
plt.title('反向传播以及梯度下降法')

plt.show()

#展示损失函数的变化
plt.scatter(np.array(list(range(len(losses))))+1,losses,s=3) #size=3
plt.xlabel('Step')
plt.ylabel('Losses')
plt.title('损失函数值随迭代周期的变化')
plt.show()

结果展示

对比结果：

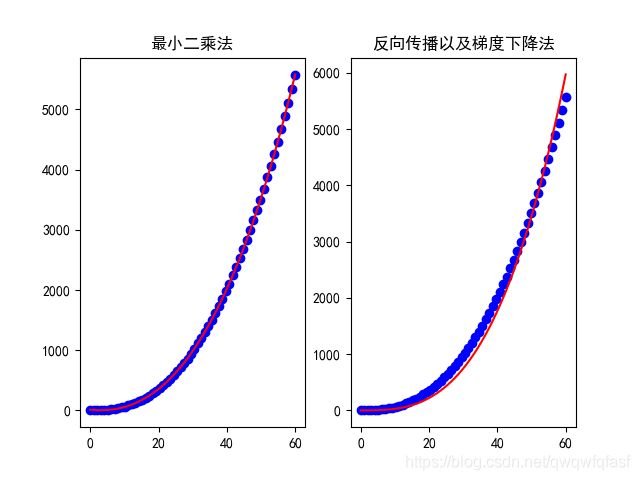
可见最小二乘法的拟合效果比梯度下降法要更好一些。

损失曲线：

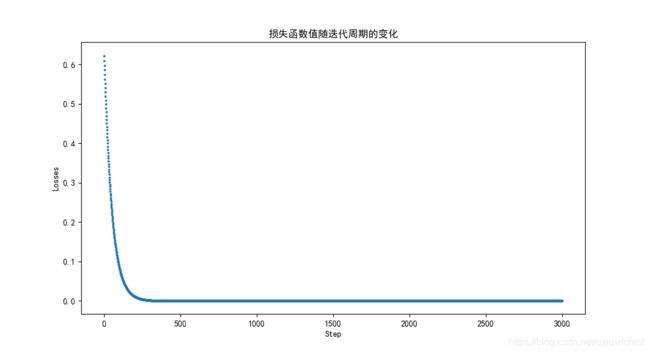
由损失曲线图可知，梯度下降算法在迭代到200次左右进入收敛。

其他发现

由上图可看出，即使两个算法求得的参数向量相差巨大，但是它们都能较好地实现对输入数据的拟合！

总结

对于所有的线性回归模型（包括多项式回归），我们都可以用最小二乘法或者梯度下降法去求解，这两种算法各有利弊，其中：
对于最小二乘法来说，它是利用线性代数里求解矩阵方程的方法得到参数向量，不需要多次迭代，也不需要调参，运算效率很高而且通常拟合效果很好，但缺点是系数矩阵并不总是可逆的，此时就需要调整系数矩阵，让它变得可逆，这样无疑会使得算法变得很复杂。
对于梯度下降法，其优点是基于梯度对参数进行更新，所以该算法不会出现失效的情况，但缺点是需要解决由输入数据带来的梯度爆炸/消失以及参数训练过程中的过拟合/欠拟合等一系列问题，这些问题需要通过一些正则化技巧以及耐心的调参来解决，同时，该算法属于迭代算法，所以运算效率比较低。

如果有什么问题，欢迎到评论区留言！！！