非常详细的范式讲解(1NF/2NF/3NF/BCNF)
范式
范式在计算机方面运用广泛,在计算机二级三级均有涉及到,今天就来讲讲范式。要是能够认真的看完,相信一定能够理解的。
在讲范式之前,我们先来了解有关范式的基本概念,听懂了有利于后面的学习。
函数依赖
首先一个好的关系模式是不会出现以下问题的:
1. 插入异常 2. 删除异常 3. 更新异常 4. 数据冗余尽量少
如果出现那是由于数据依赖,其中数据依赖分为:函数依赖,多值依赖,连接依赖等等。
所以,当关系模式出现问题,解决方法为——规范化理论(找到关系模式中不适合的数据依赖,并消除它们)
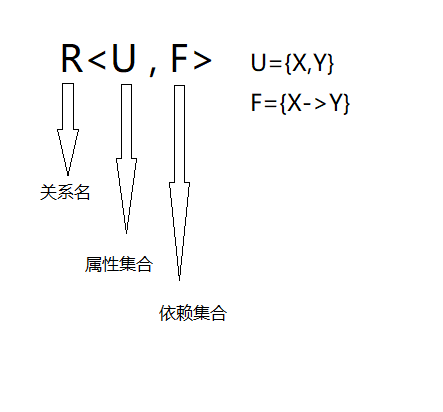
在范式这里经常使用函数依赖。那么什么是函数依赖呢?关系R中的属性X,R 中的属性 Y 只有唯一值与之对应,则称 X 函数决定 Y 或称 Y 函数依赖于 X ,记作 X—>Y。其中,X 称为决定因素。以下关系模型经常简化为R
这里给出一个例子,后面就根据这个例子来讲解。
非常主要
在函数依赖中还有以下几种分类:
1. 平凡函数依赖和非平凡函数依赖
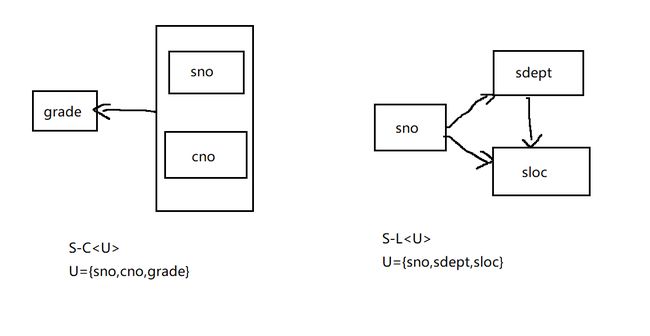
(1)X→Y且Y∉X,则X→Y是非平凡函数依赖。例如 (sno,cno)→grade
(2)X→Y且Y∈X,则X→Y是平凡函数依赖。例如 (sno,cno)→sno, (sno,cno)→cno
在任意一关系模式下,平凡函数依赖必然成立,所以,在属性之间的函数依赖关系一般讨论非平 凡函数依赖。
2. 完全函数依赖和部分函数依赖
(1)X→Y,在x的真子集 X’,Y均不依赖于X’,则称Y完全函数依赖于X。在箭头上面加上F。
(2)X→Y,在x的真子集 X’,Y存在依赖于X’,则称Y完全函数依赖于X。在箭头上面加上P。
例如以下的例子,
3. 传递函数依赖
X→Y,Y→Z 所以 X→Z,Z传递函数依赖于X。
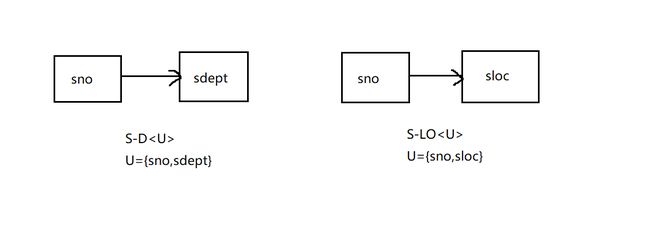
例如,sno→sdept,sdept→sloc,所以sno→sloc。
码
K是关系R
1. 候选码
若U完全函数依赖于K,则K称为R的一个候选码(换言之,一个候选码能推出所有属性)。
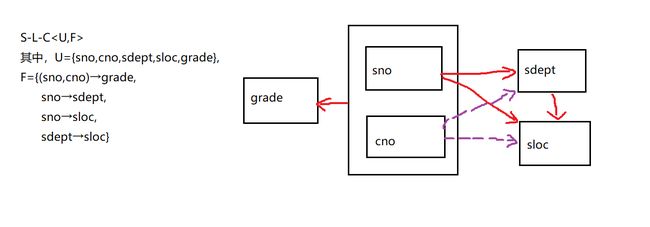
例如(sno , cno)就是关系S-L-C的候选码,因为sno和cno能推出S-L-C的所有元素
注意:一个关系中可能有多个候选码
2. 主码和主属性
主码:在一个或者多个候选码中选取其中一个作为主码。
注意:在任意一个表中都有主码,在建表中指定,如果没有指定则所有属性集合作为主码
主属性:包含在任何一个候选码中的属性(换言之,所有候选码中的属性的集合,因为有可能存在多个候选码)
3. 外码
属性X并非关系模式R的候选码,但是X是另一个关系模式的候选码。
范式
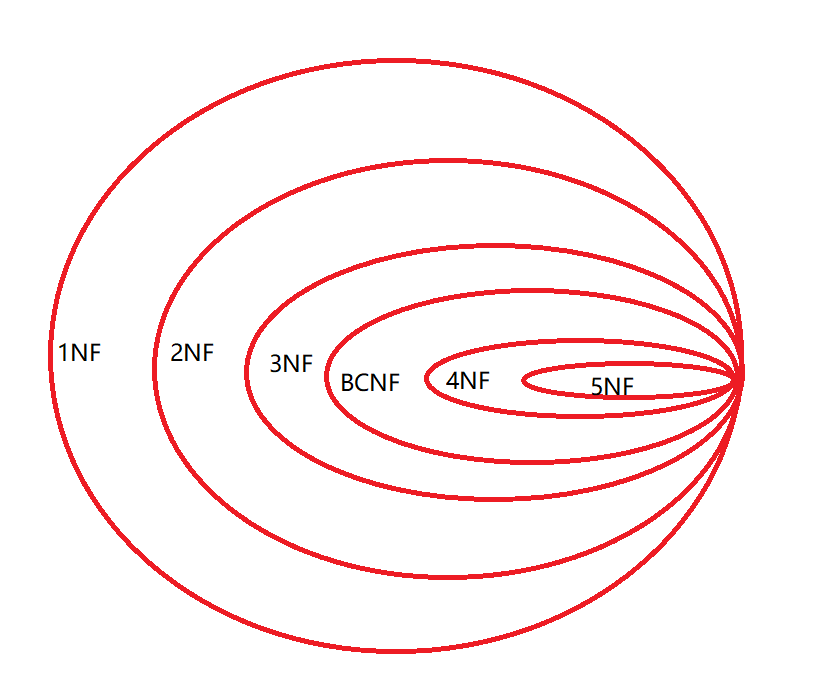
范式是符合某一种级别的关系模式的集合。下图就是表现范式级别(低范式包含高范式)。
满足高范式的同时,也一定满足低范式。
1. 一范式——1NF
一关系模式R的所有属性都是不可分的基本数据项(即表中不能再有表)。则R∈1NF。第一范式是对关系模式的最低要求,如果一个关系模式不满足1NF则不能称为关系模式。
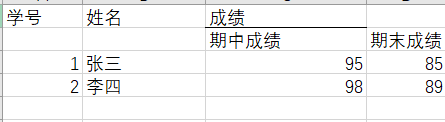
例如,以下这个关系就不满足1NF,因为“成绩”还能在分为“期中成绩”和“期末成绩”。
当然,S-L-C满足1NF,它中的元素都是不能再分。
2. 二范式——2NF
若R∈1NF,并且不存在非主属性部分依赖于R的候选码,则R∈2NF。
这里还有很多的说法,还可以说每一个非主属性都完全函数依赖于R的候选码。
例如上述例子
sdept和sloc部分函数依赖于S-L-C的候选码(sno,cno),所以S-L-C不满足2NF。
则会出现问题:
插入异常:假设学号sno=123,专业sdept=IS,宿舍sloc=N的学生还没有选课(则表示cno为空),则该学生无法将学生信息录入进系统。(因为cno为主属性,不能为空)。
删除异常:假设一学生只选了一节课,但是现在他想将这门课退了,则将需要将这门课在这名学生系统中删除,但是在删除时,会把该学生的其它信息也会删除(因为cno为主属性)。
数据冗余大:假设一学生选了10节课,则sdept和sloc也会重复10次。
修改复杂:因为数据冗余大,则修改也会复杂。
所以S-L-C不是一个很好的关系模式,所以我们需要将S-L-C分解,消除sdept和sloc对(sno,cno)的部分函数依赖。
得到S-C和S-L,其中S-C的候选码为(sno , cno),非主属性grade完全函数依赖于(sno , cno)所以S-C∈2NF,同理非S-L的非主属性sdept完全函数依赖于候选码sno,同理,sloc完全函数依赖于候选码sno,所以S-L∈2NF。
分解完毕,现在就解决上述的问题了。
综上,2NF要注意非主属性对候选码的函数依赖,如果存在着部分函数依赖,则不满足2NF,反之,满足2NF。
3. 三范式——3NF
简单的说,在满足2NF的基础上,关系模式中不存在传递函数依赖。
例如在上述例子中的S-L,存在sno→sdept,sdept→sloc,并且有sno→sloc,所以存在函数传递依赖,不满足3NF。
并且在2NF任然存在问题,以上述S-L为例:
- 插入异常:若刚成立一个专业(sdept),但是还没有学生(sno),则无法向数据库中录入sdept和sloc。
- 删除异常:若一个专业的学生全部毕业,需要将学号删除时,则sdept和sloc也会被删除。
- 数据冗余大:若同一个专业的学生住在一起(即sloc都相同),就会有很多的sloc重复。
- 修改复杂:因为数据冗余大,所以要修改时很复杂。
所以S-L也不是一个很好的关系模式,需要将其分解,也就是让S-L满足3NF。
解决办法:消除传递函数依赖。
这样就解决了2NF存在的问题了。
这里补充一个知识点:
1. 所有高范式成立,则低范式也一定成立,即若R∈3NF,则一定R∈2NF。
2. 若R∈3NF,则R的**每一个非主属性既不部分函数依赖于候选码,也不传递函数依赖于候选码**。
4. BCNF
没有任何属性(主属性和非主属性)对候选码的部分函数依赖和传递函数依赖。
以下例子,
因为候选码为(S,T)和(S,J),所以主属性为(S,T,J),不存在非主属性。所以一定满足3NF。
但是这里存在主属性对候选码的部分函数依赖,所以不满足BCNF。
5. 4NF和5NF
当然还有4NF和5NF,原理和以上的一样,不是很重要。
这里就简单的了解一下,
4NF:当R∈BCNF,消除非平凡且非函数依赖的多值依赖。
5NF:当R∈4NF,消除不是由候选码所蕴含的连接依赖。如果关系模式R中的每一个连接依赖均由R的候选码所隐含
总结
在范式的学习中,一定要把知识点弄清,例如部分函数依赖,完全函数依赖,候选码,主属性等等。把原理搞懂了,很有利于后面的学习。其实搞懂了范式还是非常简单的。