基于混沌权重和精英引导的鲸鱼优化算法

一、理论基础

1、基本的WOA

请参考这里。

2、AWOA

（1）精英个体引导机制

为了加快对猎物搜索的速度，提出一种精英个体引导机制。选取当前种群最优个体作为精英个体引导种群位置更新，位置更新公式变为$$\mathbf{X}(t+1)={\mathbf{X}}_p(t)-\mathbf{d}\mathbf{i}\mathbf{r}\cdot \mathbf{A}\cdot \mathbf{D}\text{\hspace{1em}(1)}$$其中，${\mathbf{X}}_p(t)$为第$t$次迭代时，种群适应度最优的个体位置。$\mathbf{d}\mathbf{i}\mathbf{r}$为种群搜索方向因子，比较当前种群最优个体的适应度值$fit({\mathbf{X}}_p(t))$与上一代种群最优个体适应度$fit({\mathbf{X}}_p(t-1))$，若$fit({\mathbf{X}}_p(t))>fit({\mathbf{X}}_p(t-1))$，则$\mathbf{d}\mathbf{i}\mathbf{r}$为单位向量，否则$\mathbf{d}\mathbf{i}\mathbf{r}$向量的每一维通过下式得到$${\mathbf{d}\mathbf{i}\mathbf{r}}_j=\{\begin{array}{l}-1,{\mathbf{A}}_j\cdot [{\mathbf{X}}_p^j(t)-{\mathbf{X}}_p^j(t-1)]>0\\ 1,else\end{array}\text{\hspace{1em}(2)}$$由式(1)、式(2)可知，精英个体使种群朝靠近最优解位置进行搜索，搜索方向因子则利用最优个体的进化反馈信息对种群的搜索方向进行调整，两者的加入使种群搜索更具有目的性，避免了因随机个体与搜索矢量$\mathbf{A}$的随机性而导致收敛速度较慢的问题。值得注意的是，精英个体的引入使得最优鲸鱼个体在鲸鱼种群搜索中扮演着领导者的角色，所以，其位置的好坏决定了种群的搜索效率，为了提高领导者的质量，在每次迭代中，对精英个体进行一次随机扰动与反向搜索操作，得到两个新的个体${\mathbf{X}}_p^{\ast },{\mathbf{X}}_p^{\ast \ast }$，其求解公式如下$${\mathbf{X}}_p^{\ast }={\mathbf{X}}_{\min }+\mathbf{r}\cdot ({\mathbf{X}}_{\max }-{\mathbf{X}}_{\min }),{\mathbf{X}}_p^{\ast \ast }={\mathbf{X}}_{\max }+{\mathbf{X}}_{\min }-{\mathbf{X}}_p^{\ast }\text{\hspace{1em}(3)}$$其中，${\mathbf{X}}_{\min },{\mathbf{X}}_{\max }$分别为搜索空间的上界和下界，$\mathbf{r}$为$[0,1]$区间的随机向量。将得到的${\mathbf{X}}_p^{\ast },{\mathbf{X}}_p^{\ast \ast }$替换种群中适应度最
差的两个个体，并更新当前种群最优个体${\mathbf{X}}_p$。

（2）混沌动态权重因子

本文引入一种计算简单的动态混沌权重因子，其表达式如下$$\omega (t+1)=4\cdot \omega (t)\cdot (1-\omega (t)),t=1,2,\cdots ,t_{\max }\text{\hspace{1em}(4)}$$其中，$\omega (1)$为$[0,1]$区间的随机数，将式(4)代入座头鲸螺旋轨迹捕食公式，并引入一个随迭代次数变化的收敛因子$\lambda$，改进后的位置更新公式如下$$\mathbf{X}(t+1)=\omega (t)\cdot \lambda \cdot {\mathbf{X}}_{\text{best}}-\mathbf{A}\cdot \mathbf{D}\text{\hspace{1em}(5)}$$$$\mathbf{X}(t+1)={\mathbf{D}}_{\text{best}}\cdot e^{bl}\cdot \cos (2\pi l)+\omega (t)\cdot \lambda \cdot \mathbf{X}(t)\text{\hspace{1em}(6)}$$$$\lambda =\frac{t_{\max }-t}{t_{\max }}\text{\hspace{1em}(7)}$$从式(4)中可知，本文选取Logistic混沌映射，利用其随机性、遍历性等优点动态调整惯性权重，使鲸鱼个体能在猎物周围进行更加精细、彻底地搜索，加快了算法的收敛速度，同时也降低了算法陷入局部最优的概率。其次，参数$\lambda$随着迭代次数的增加而自适应的减小，能有效控制权重因子混沌变化的范围，缩小鲸鱼种群的寻优区域，使算法迅速收敛于全局最优解，保证了算法的收敛性。

（3）改进算法步骤

具体步骤如下图所示。

二、仿真实验与分析

将改进鲸鱼优化算法(AWOA)与粒子群优化算法(PSO)、基本鲸鱼优化算法(WOA)进行对比，以文献[1]中100维的F1~F4为例。种群规模设置为30，最大迭代次数为500，为了减少算法的随机性对结果的影响，3种算法均连续独立运行30次，记录30次实验中各测试函数最优适应度值的最差值、最优值、平均值和标准差。
结果显示如下：

函数：F1
AWOA：最差值: 0,最优值:0,平均值:0,标准差:0
WOA：最差值: 8.3724e-69,最优值:4.2314e-84,平均值:3.0815e-70,标准差:1.5267e-69
PSO：最差值: 4380.8964,最优值:2367.0076,平均值:3324.7732,标准差:489.4198
函数：F2
AWOA：最差值: 0,最优值:0,平均值:0,标准差:0
WOA：最差值: 5.9389e-48,最优值:3.4065e-56,平均值:2.1512e-49,标准差:1.082e-48
PSO：最差值: 103.4247,最优值:56.7885,平均值:77.0152,标准差:10.9677
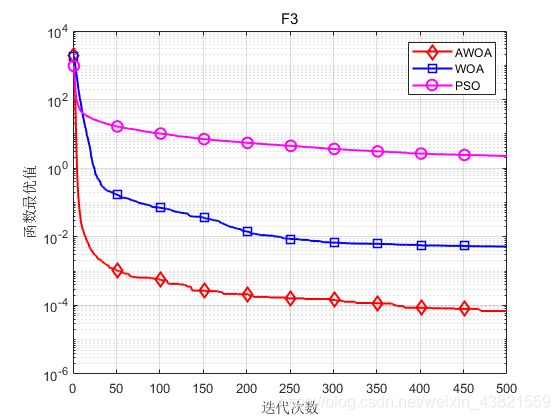
函数：F3
AWOA：最差值: 0.00027774,最优值:7.7146e-07,平均值:6.8705e-05,标准差:6.7831e-05
WOA：最差值: 0.035186,最优值:7.7724e-05,平均值:0.0052348,标准差:0.0072841
PSO：最差值: 4.6512,最优值:1.019,平均值:2.2626,标准差:0.69413
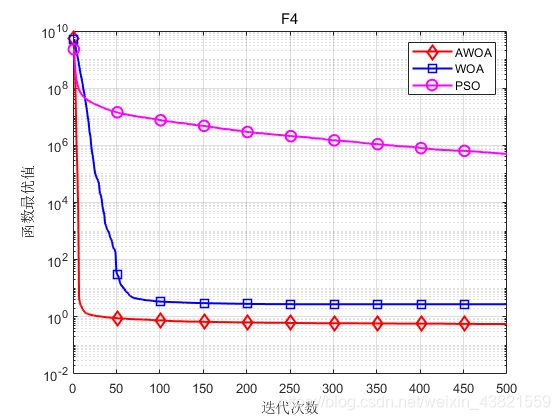
函数：F4
AWOA：最差值: 0.91411,最优值:0.31166,平均值:0.55991,标准差:0.12653
WOA：最差值: 5.5307,最优值:0.90387,平均值:2.7674,标准差:1.142
PSO：最差值: 1250000.0617,最优值:95123.344,平均值:501609.5712,标准差:275332.9328

结果表明，与基本的WOA和粒子群算法相比，本文提出的AWOA具有更高的收敛速度、求解精度和稳定性。

三、参考文献

[1] 黄辉先, 张广炎, 陈思溢, 等. 基于混沌权重和精英引导的鲸鱼优化算法[J]. 传感器与微系统, 2020, 39(5): 113-116.