增强型麻雀搜索算法
文章目录
- 一、理论基础
-
- 1、麻雀搜索算法SSA
- 2、增强型麻雀搜索算法ESSA
-
- (1)Gauss映射
- (2)动态惯性权重
- (3)学生t分布扰动
- (4)越界处理方法
- (5)ESSA算法流程
- 二、仿真实验结果与分析
- 三、参考文献
一、理论基础
1、麻雀搜索算法SSA
请参考这里。
2、增强型麻雀搜索算法ESSA
(1)Gauss映射
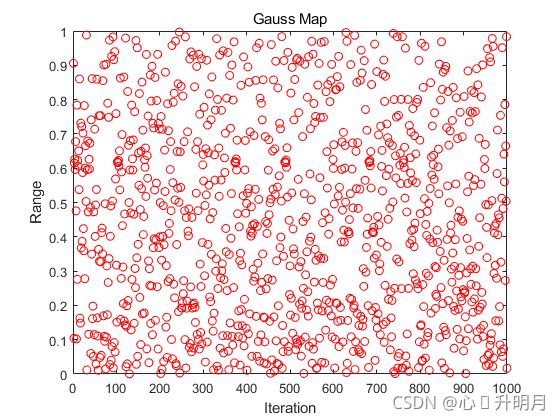
本文将混沌映射模型引入SSA算法的初始化阶段,利用Gauss映射所具有规律性、随机性、遍历性等特征,通过建立映射关系将映射产生的混沌序列转换至SSA算法的解空间代替原始种群,从而减弱随机种群带来的不确定性影响,为全局寻优奠定良好的基础。Gauss映射的数学表达式为: x k + 1 = { 0 , x k = 0 1 x k mod ( 1 ) , x k ≠ 0 (1) x_{k+1}=\begin{dcases}0,\quad\quad\quad\quad\,\,\,\,\, x_k=0\\\frac{1}{x_k\text{mod}(1)},\quad x_k≠0\end{dcases}\tag{1} xk+1=⎩⎨⎧0,xk=0xkmod(1)1,xk=0(1) 1 x k mod ( 1 ) = 1 x k − [ 1 x k ] (2) \frac{1}{x_k\text{mod}(1)}=\frac{1}{x_k}-\left[\frac{1}{x_k}\right]\tag{2} xkmod(1)1=xk1−[xk1](2)其中, mod \text{mod} mod为求余函数, [ ] [\,\,] []代表取整, x = ( x 1 , x 2 , ⋯ , x d ) x=(x_1,x_2,\cdots,x_d) x=(x1,x2,⋯,xd)为高斯映射产生的混沌序列, d d d表示维度。图1为Gauss映射在 [ 0 , 1 ] [0,1] [0,1]区间内产生的散点分布图。
(2)动态惯性权重
为了进一步平衡算法在不同迭代阶段的搜索方式,在发现者位置更新公式中引入动态变化的惯性权重 ω \omega ω,随着迭代的增加,自适应线性递减的 ω \omega ω将对式(1)中发现者位置 X i , j T X_{i,j}^T Xi,jT的参与程度进行动态调控,尤其在迭代后期使发现者可以更加有效的进行局部搜索,加强了算法在解空间的邻域搜索能力。新的发现者位置更新公式及 ω \omega ω的计算式为: X i , j T + 1 = { ω T ⋅ X i , j T ⋅ exp ( − i α ⋅ M a x I t e r ) , R 2 < S T ω T ⋅ X i , j T + Q ⋅ L , R 2 ≥ S T (3) X_{i,j}^{T+1}=\begin{dcases}\omega_T\cdot X_{i,j}^T\cdot\exp\left(-\frac{i}{\alpha\cdot MaxIter}\right),\quad R_2
(3)学生t分布扰动
利用t分布调节 ν \nu ν值大小可以达到不同种类分布的特性,将不断变化的迭代次数 I t e r a t i o n Iteration Iteration赋予 ν \nu ν值以产生不同的变异幅频。每次循环后,对麻雀位置使用学生t分布模型进行扰动更新如式(5)所示: X i ′ = { X i + X i ⊗ t ( I t e r a t i o n ) , r a n d < p X i , o t h e r w i s e (5) X_i'=\begin{dcases}X_i+X_i\otimes \text{t}(Iteration),\quad rand rand<p
(4)越界处理方法
本文采用一种随机回归的越界处理操作对越界量进行处理,具体式(6)所示: x i ′ = { u b − min ( x i − u b , u b − l b ) ⋅ γ , x i > u b l b + min ( l b − x i , u b − l b ) ⋅ γ , x i < l b (6) x_i'=\begin{dcases}ub-\min(x_i-ub,ub-lb)\cdot\gamma,\quad x_i>ub\\lb+\min(lb-x_i,ub-lb)\cdot\gamma,\quad\,\,\,\, x_i
(5)ESSA算法流程
二、仿真实验结果与分析
为验证ESSA的寻优性能,选取了文献[2]提出的基于粒子群算法和Tent映射的混合灰狼优化算法(Grey Wolf Optimization Algorithm based on Particle Swarm Optimization, PSO_GWO),文献[3]提出的基于精英反向学习的黄金正弦鲸鱼算法(Elite Opposition-Based Golden-Sine Whale Optimization Algorithm, EGolden-SWOA),文献[4]提出的融合柯西变异和反向学习策略的改进麻雀搜索算法1(Improved Sparrow Algorithm combining Cauchy mutation and Opposition-based learning, ISSA1),文献[5]提出的混合正余弦搜索和Lévy飞行的改进麻雀搜索算法2(Improved Sparrow Search Algorithm, ISSA2)。为保证计算效率,本文统一设置种群大小为30、迭代次数为100,仿真实验对比原算法并使每种算法在基准函数上各独立进行30次。以文献[1]中表2中的f1、f2(单峰函数/30维)、f6、f7(多峰函数/30维)、f12、f13(固定维度多峰函数)为例,结果显示如下:



函数:F1
PSO_GWO:最差值: 2.0021e-26,最优值:9.726e-30,平均值:1.376e-27,标准差:4.2399e-27,秩和检验:7.8787e-12
EGolden_SWOA:最差值: 8.0633e-36,最优值:6.3806e-41,平均值:6.2778e-37,标准差:1.9139e-36,秩和检验:7.8787e-12
SSA:最差值: 1.3423e-44,最优值:0,平均值:5.1104e-46,标准差:2.4625e-45,秩和检验:9.2307e-11
ISSA1:最差值: 4.699e-132,最优值:3.551e-171,平均值:1.5663e-133,标准差:8.5792e-133,秩和检验:7.8787e-12
ISSA2:最差值: 1.1133e-121,最优值:2.9193e-129,平均值:4.1834e-123,标准差:2.0301e-122,秩和检验:7.8787e-12
ESSA:最差值: 1.326e-182,最优值:0,平均值:4.42e-184,标准差:0,秩和检验:1
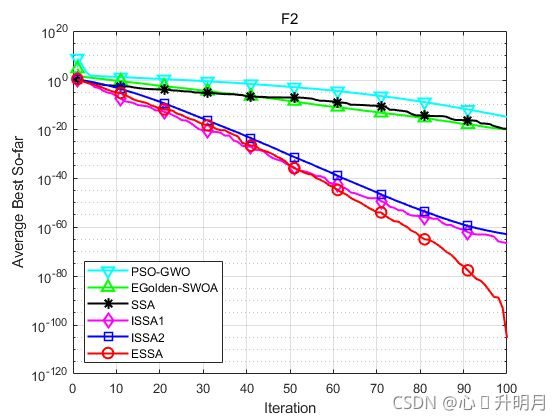
函数:F2
PSO_GWO:最差值: 4.0295e-15,最优值:5.7804e-17,平均值:9.361e-16,标准差:9.2046e-16,秩和检验:2.3657e-12
EGolden_SWOA:最差值: 9.6798e-20,最优值:1.2634e-23,平均值:6.2139e-21,标准差:1.899e-20,秩和检验:2.3657e-12
SSA:最差值: 3.6239e-19,最优值:0,平均值:1.228e-20,标准差:6.6133e-20,秩和检验:6.3581e-11
ISSA1:最差值: 7.2808e-66,最优值:9.0882e-89,平均值:2.44e-67,标准差:1.3291e-66,秩和检验:2.3657e-12
ISSA2:最差值: 9.4317e-63,最优值:1.2637e-68,平均值:1.1256e-63,标准差:2.3456e-63,秩和检验:2.3657e-12
ESSA:最差值: 1.8185e-104,最优值:0,平均值:6.0617e-106,标准差:3.3201e-105,秩和检验:1
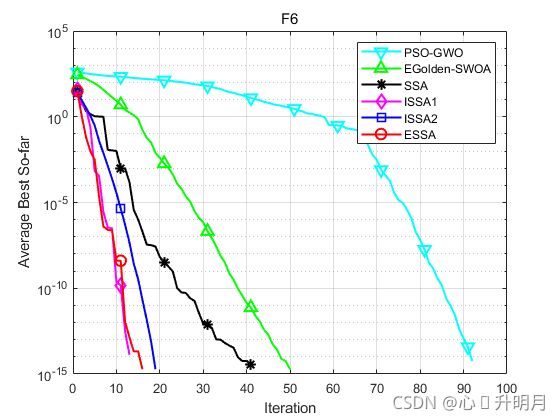
函数:F6
PSO_GWO:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
EGolden_SWOA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
SSA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
ISSA1:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
ISSA2:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
ESSA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数:F7
PSO_GWO:最差值: 3.2863e-14,最优值:4.4409e-15,平均值:6.9278e-15,标准差:6.2691e-15,秩和检验:2.0666e-13
EGolden_SWOA:最差值: 4.4409e-15,最优值:8.8818e-16,平均值:3.4935e-15,标准差:1.5979e-15,秩和检验:5.3591e-09
SSA:最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0,秩和检验:NaN
ISSA1:最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0,秩和检验:NaN
ISSA2:最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0,秩和检验:NaN
ESSA:最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0,秩和检验:NaN
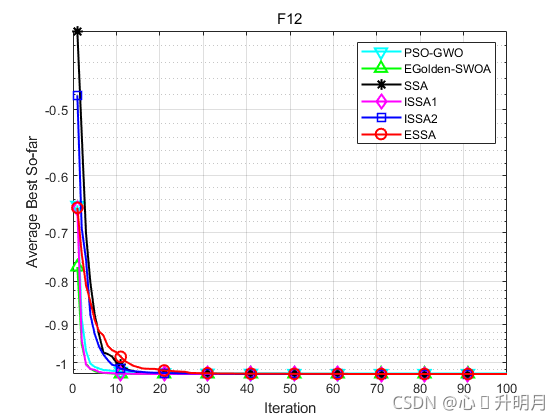
函数:F12
PSO_GWO:最差值: -1.0279,最优值:-1.0314,平均值:-1.0302,标准差:0.0010526,秩和检验:3.0199e-11
EGolden_SWOA:最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:1.3003e-07,秩和检验:3.8202e-10
SSA:最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:3.8746e-09,秩和检验:3.0199e-11
ISSA1:最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:1.8804e-10,秩和检验:3.0199e-11
ISSA2:最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:3.9383e-08,秩和检验:4.0772e-11
ESSA:最差值: -1.0315,最优值:-1.0316,平均值:-1.0316,标准差:2.4012e-05,秩和检验:1
函数:F13
PSO_GWO:最差值: 0.77143,最优值:0.39853,平均值:0.48908,标准差:0.079794,秩和检验:3.0199e-11
EGolden_SWOA:最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:1.5889e-06,秩和检验:1.2541e-07
SSA:最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:9.5566e-08,秩和检验:5.4941e-11
ISSA1:最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:1.866e-08,秩和检验:3.3384e-11
ISSA2:最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:1.9399e-07,秩和检验:8.9934e-11
ESSA:最差值: 0.39833,最优值:0.39789,平均值:0.39792,标准差:7.9989e-05,秩和检验:1
实验结果验证了改进策略的有效性。
三、参考文献
[1] 刘睿, 莫愿斌. 增强型麻雀搜索算法及其工程优化应用[J/OL]. 小型微型计算机系统: 1-10 [2021-11-10].
[2] 滕志军, 吕金玲, 郭力文, 等. 一种基于Tent映射的混合灰狼优化的改进算法[J]. 哈尔滨工业大学学报, 2018, 50(11): 40-49.
[3] 肖子雅, 刘升. 精英反向黄金正弦鲸鱼算法及其工程优化研究[J]. 电子学报, 2019, 47(10): 2177-2186.
[4] 毛清华, 张强. 融合柯西变异和反向学习的改进麻雀算法[J]. 计算机科学与探索, 2021, 15(6): 1155-1164.
[5] 毛清华, 张强, 毛承成, 等. 混合正弦余弦算法和Lévy飞行的麻雀算法[J]. 山西大学学报(自然科学版), 2021, 44(6): 1086-1091.
