手写感知机，KNN，决策树（ID3）对iris（鸢尾花）进行二分类

手写感知机，KNN，决策树（ID3），贝叶斯，逻辑斯蒂回归（Lgistic),SVM对iris（鸢尾花）进行二分类

我们统计学习这门课期末也是要求使用不同的二分类方法对同一个数据集进行分类并且进行比较。于是我在网上看了很多都没有相关的文章，因此我在这里记录一下不同的方法对同一个数据集的分类与比较。
我们使用的是iris数据集，这个数据集在sklearn库里面是有的，一共150行数据，分为三类。在这个实验中我们采用前100行进行实验，刚好两个类嘛。
对数据的处理有着不同的方法，这些就看情况而选。数据集我会放在最后。声明：代码都是找的，然后在上面进行了自己需要的修改，链接在下面。

1.感知机

感知机概念啥的我就不在这说了。
主要思想是通过判断是否还有误分类点，误分类点判断就是y(wx+b)<=0,当有误分类点时，就进行梯度更行，一直到全部都正确分类才行。但需要注意的是，这个数据集要是线性可分的，如果不可分的话会导致一致进行更新从而进入死循环。当然，我们可以通过代码设置训练模型时允许误分类几个点的个数，从而使模型损失度最小。这个iris的数据集很好分，所以一般用不了多久结果就出来了。噢对了，这样导致的结果是测试集的准确率都会为1，所以我在代码里面加了点噪声，从而再次进行判断与比较。
代码详解与数据处理都在代码里面了。

# 感知机（perceptron）是二分类的线性分类模型，其中输入是实例的特征向量，输出是类别，
# 类别取+1和-1二值。感知机的目标是求出一个超平面将训练数据进行线性划分。
from sklearn import metrics
from sklearn.model_selection import train_test_split

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris


iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target   #将标签加在后面

class Model():
    def __init__(self):
        # 一共训练两个特征需要2个权重参数，data数据是3列，第三列是数据标签
        self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.05

    def sign(self, x, w, b):
        y = np.dot(x, w) + b
        return y

    # 使用随机梯度进行拟合
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                # 如果分类错误,就进行梯度更新
                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate * np.dot(y, X)
                    self.b = self.b + self.l_rate * y
                    wrong_count += 1

            if wrong_count == 0:  # 如果全都分类正确,wrong_count值为0,则停止拟合
                is_wrong = True
        return 'Perceptron Model'

    def score(self):
        pass
# 实现感知机
# 取2,3两列特征，-1表示标签
data = np.array(df.iloc[:100])
dataDiyList = [[5,2.8,1.9,0.3,0],[6.2,2.8,1.9,0.3,1],[5.8,2.3,3.4,0.3,1],[5,2.8,1.9,0.3,0],[7.0,2.0,3.4,0.2,1],
               [5.0,3.4,1.5,0.8,0],[4.78,3.1,1.7,0.9,1],[5.6,2.9,3.4,.99,0]]
dataDiyAaary = np.array(dataDiyList)
data = np.row_stack((data,dataDiyAaary))

X = data[:, :-1]  # 取出特征
y = data[:, -1]  # 取出标签
y = np.array([1 if i == 1 else -1 for i in y])  # y表示类别，正常取值是0和1，把0类别的值改为-1

for i in range(1,10):
    print("第%d轮---------------\n"%i)
    X_train, X_test, y_train, y_test = train_test_split( \
        X, y, test_size=0.50, random_state=10, shuffle=True)  # random_state不为0为了使每次取的数据不一样
    # 拟合
    perceptron = Model()
    perceptron.fit(X_train, y_train)
    y_predict = perceptron.sign(X_test, perceptron.w, perceptron.b)
    y_predict = np.array([1 if i > 0 else -1 for i in y_predict])  # y表示类别，正常取值是0和1，把0类别的值改为-1
    print(y_predict)
    M = metrics.confusion_matrix(y_predict, y_test)
    print('混淆矩阵:\n', M)
    # 精确率、召回率
    n = len(M)
    for i in range(n):
        rowsum, colsum = sum(M[i]), sum(M[r][i] for r in range(n))
        precision = M[i][i] / float(colsum)
        recall = M[i][i] / float(rowsum)
        F1 = precision * recall * 2 / (precision + recall)
        print('%d类别的精确率: %s' % (i, precision), '%d类别的召回率: %s' % (i, recall), '%d类别的F1值: %s' % (i, F1))
    print("模型精度(准确率)：{:.5f}".format(np.mean(y_predict == y_test)))
    print('权重:', perceptron.w[0], perceptron.w[1], perceptron.w[2], perceptron.w[3])
    print('偏置:', perceptron.b)

结果：代码的讲解也很清晰，结果就是再有噪声的情况下，尽管使用少量的数据进行训练，效果也很好，主要是因为这个数据集很好分。

2.KNN

KNN的思想很简单，也不需要训练，就是给你一个点，然后你去求它与所有点的距离，然后取K个最近的点进行投票。这K个里面哪一类的个数最多，就将这个点判给哪一类。这里面需要注意对数据进行归一化处理。
代码：

# -*- coding:utf-8 -*-
import pandas as pd
import numpy as np
import operator as opt
from sklearn import metrics
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target   #将标签家在后面


#考虑到不同特征值范围差别很大的影响，可对这类数据进行最大最小值标准化数据集
def normData(dataset):
    maxVals = dataset.max(axis=0) #求列的最大值
    minVals = dataset.min(axis=0) #求列的最小值
    ranges = maxVals - minVals
    retData = (dataset - minVals) / ranges
    return retData, minVals, ranges

#KNN,欧式距离
def kNN(dataset, labels, testdata, k):
    distSquareMat = (dataset - testdata) ** 2 #计算差值的平方
    distSquareSums = distSquareMat.sum(axis=1) #求每一行的差值平方和
    distances = distSquareSums ** 0.5 #开根号，得出每个样本到测试点的距离
    sortedIndices = distances.argsort()  #array.argsort(),默认axis=0从小到大排序，得到排序后的下标位置
    indices = sortedIndices[:k] #取距离最小的k个值对应的小标位置
    labelCount = {} #存储每个label的出现次数
    for i in indices:  #遍历下标,里面的值
        label = labels[i]
        labelCount[label] = labelCount.get(label, 0) + 1 #次数加1,dict.get(k, val)获取字典中k对应的值,没有k,则返回val

    sortedCount = sorted(labelCount.items(), key=opt.itemgetter(1), reverse=True) #operator.itemgetter(),结合sorted使用,可按不同的区域进行排序
    return sortedCount[0][0] #返回最多的一个label

#主函数
if __name__ == "__main__":
    data = np.array(df.iloc[:100])
    dataDiyList = [[5, 2.8, 1.9, 0.3, 1], [6.2, 2.8, 1.9, 0.3, 0], [5.8, 2.3, 3.4, 0.3, 0], [5, 2.8, 1.9, 0.3, 1],[7.0, 2.0, 3.4, 0.2, 0],
                   [5.0, 3.4, 1.5, 0.8, 0], [4.78, 3.1, 1.7, 0.9, 0], [5.6, 2.9, 3.4, .99, 0]]
    dataDiyAaary = np.array(dataDiyList)
    data = np.row_stack((data, dataDiyAaary))
    X = data[:, :-1]  # 取出特征
    y = data[:, -1]  # 取出标签
    for i in range (1,10):
        print("第%d轮---------------\n" % i)
        X_train, X_test, y_train, y_test = train_test_split( \
            X, y, test_size=0.50, random_state=i, shuffle=True)  # random_state不为0为了使每次取的数据不一样
        y_pred = []

        for i in range(len(X_test)):
            onedata = X_test[i]
            result = kNN(X_train, y_train, onedata, 2)
            y_pred.append(result)
        print(y_pred)
        M = metrics.confusion_matrix(y_pred, y_test)
        print('混淆矩阵:\n', M)
        n = len(M)
        for i in range(n):
            rowsum, colsum = sum(M[i]), sum(M[r][i] for r in range(n))
            precision = M[i][i] / float(colsum)
            recall = M[i][i] / float(rowsum)
            F1 = precision * recall * 2 / (precision + recall)
            print('%d类别的精确率: %s' % (i, precision), '%d类别的召回率: %s' % (i, recall), '%d类别的F1值: %s' % (i, F1))
        print("模型精度(准确率)：{:.5f}".format(np.mean(y_pred == y_test)))

3 决策树

决策树的关键点在于每次选取特征是选取的信息增益最大的那个特征。最基本的也就是ID3了，后面衍生的有C4.5，CART，以及剪枝操作。这里我们通过ID3进行写。这个代码里面分别对离散的值进行了处理（比如帅不帅，有没有钱，瓜甜不甜这些类型），还有连续的（1，2，3，4)这种。这两种不同类型需要不同的方式进行处理。这里面都有，还有将生成的树保存以及画出来的函数。这个代码是我在网上找的，我实在手写不出来，看懂他们写的就行，敬佩大佬。
代码：

#https://blog.csdn.net/kai123wen/article/details/105769970

#https://github.com/login?return_to=%2Fjiajia0%2FMachineLearningTopic
import collections
import random
import string
from math import log
import pandas as pd
import operator
from 期末.二分类花 import treePlotter


def calcShannonEnt(dataSet):
    """
    计算给定数据集的信息熵(香农熵)
    :param dataSet:
    :return:
    """
    # 计算出数据集的总数
    numEntries = len(dataSet)

    # 用来统计标签
    labelCounts = collections.defaultdict(int)

    # 循环整个数据集，得到数据的分类标签
    for featVec in dataSet:
        # 得到当前的标签
        currentLabel = featVec[-1]

        # 将对应的标签值加一
        labelCounts[currentLabel] += 1

    # 默认的信息熵
    shannonEnt = 0.0

    for key in labelCounts:
        # 计算出当前分类标签占总标签的比例数
        prob = float(labelCounts[key]) / numEntries

        # 以2为底求对数
        shannonEnt -= prob * log(prob, 2)

    return shannonEnt


def splitDataSetForSeries(dataSet, axis, value):
    """
    按照给定的数值，将数据集分为不大于和大于两部分
    :param dataSet: 要划分的数据集
    :param i: 特征值所在的下标
    :param value: 划分值
    :return:
    """
    # 用来保存不大于划分值的集合
    eltDataSet = []
    # 用来保存大于划分值的集合
    gtDataSet = []
    # 进行划分，保留该特征值
    for feat in dataSet:
        if feat[axis] <= value:
            eltDataSet.append(feat)
        else:
            gtDataSet.append(feat)

    return eltDataSet, gtDataSet


def splitDataSet(dataSet, axis, value):
    """
    按照给定的特征值，将数据集划分
    :param dataSet: 数据集
    :param axis: 给定特征值的坐标
    :param value: 给定特征值满足的条件，只有给定特征值等于这个value的时候才会返回
    :return:
    """
    # 创建一个新的列表，防止对原来的列表进行修改
    retDataSet = []

    # 遍历整个数据集
    for featVec in dataSet:
        # 如果给定特征值等于想要的特征值
        if featVec[axis] == value:
            # 将该特征值前面的内容保存起来
            reducedFeatVec = featVec[:axis]
            # 将该特征值后面的内容保存起来，所以将给定特征值给去掉了
            reducedFeatVec.extend(featVec[axis + 1:])
            # 添加到返回列表中
            retDataSet.append(reducedFeatVec)

    return retDataSet


def calcInfoGainForSeries(dataSet, i, baseEntropy):
    """
    计算连续值的信息增益
    :param dataSet:整个数据集
    :param i: 对应的特征值下标
    :param baseEntropy: 基础信息熵
    :return: 返回一个信息增益值，和当前的划分点
    """

    # 记录最大的信息增益
    maxInfoGain = 0.0

    # 最好的划分点
    bestMid = -1

    # 得到数据集中所有的当前特征值列表
    featList = [example[i] for example in dataSet]

    # 得到分类列表
    classList = [example[-1] for example in dataSet]

    dictList = dict(zip(featList, classList))

    # 将其从小到大排序，按照连续值的大小排列
    sortedFeatList = sorted(dictList.items(), key=operator.itemgetter(0))

    # 计算连续值有多少个
    numberForFeatList = len(sortedFeatList)

    # 计算划分点，保留三位小数,将第i个和i+1个第一列的值加起来除2，也就是找出大于小于得分界线。
    midFeatList = [round((sortedFeatList[i][0] + sortedFeatList[i + 1][0]) / 2.0, 3) for i in
                   range(numberForFeatList - 1)]

    # 计算出各个划分点信息增益
    for mid in midFeatList:
        # 将连续值划分为不大于当前划分点和大于当前划分点两部分
        eltDataSet, gtDataSet = splitDataSetForSeries(dataSet, i, mid)

        # 计算两部分的特征值熵和权重的乘积之和
        #条件熵
        newEntropy = len(eltDataSet) / len(dataSet) * calcShannonEnt(eltDataSet) + len(gtDataSet) / len(
            dataSet) * calcShannonEnt(gtDataSet)

        # 计算出信息增益
        infoGain = baseEntropy - newEntropy

        # print('当前划分值为：' + str(mid) + '，此时的信息增益为：' + str(infoGain))
        if infoGain > maxInfoGain:
            bestMid = mid
            maxInfoGain = infoGain

    return maxInfoGain, bestMid


def calcInfoGain(dataSet, featList, i, baseEntropy):
    """
    计算信息增益
    :param dataSet: 数据集
    :param featList: 当前特征列表
    :param i: 当前特征值下标
    :param baseEntropy: 基础信息熵
    :return:
    """
    # 将当前特征唯一化，也就是说当前特征值中共有多少种
    uniqueVals = set(featList)

    # 新的熵，代表当前特征值的熵
    newEntropy = 0.0

    # 遍历现在有的特征的可能性
    for value in uniqueVals:
        # 在全部数据集的当前特征位置上，找到该特征值等于当前值的集合
        subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value)
        # 计算出权重
        prob = len(subDataSet) / float(len(dataSet))
        # 计算出当前特征值的熵
        newEntropy += prob * calcShannonEnt(subDataSet)

    # 计算出“信息增益”
    infoGain = baseEntropy - newEntropy

    return infoGain


def chooseBestFeatureToSplit(dataSet, labels):
    """
    选择最好的数据集划分特征，根据信息增益值来计算，可处理连续值
    :param dataSet:
    :return:
    """
    # 得到数据的特征值总数
    numFeatures = len(dataSet[0]) - 1

    # 计算出基础信息熵,计算出H(D).
    baseEntropy = calcShannonEnt(dataSet)

    # 基础信息增益为0.0
    bestInfoGain = 0.0

    # 最好的特征值
    bestFeature = -1

    # 标记当前最好的特征值是不是连续值
    flagSeries = 0

    # 如果是连续值的话，用来记录连续值的划分点
    bestSeriesMid = 0.0

    # 对每个特征值进行求信息熵
    for i in range(numFeatures):

        # 得到数据集中所有的当前特征值列表,第i列数据
        featList = [example[i] for example in dataSet]
        #分别处理连续值和不连续的
        if isinstance(featList[0], str):
            infoGain = calcInfoGain(dataSet, featList, i, baseEntropy)
        else:
            # print('当前划分属性为：' + str(labels[i]))
            infoGain, bestMid = calcInfoGainForSeries(dataSet, i, baseEntropy)

        # print('当前特征值为：' + labels[i] + '，对应的信息增益值为：' + str(infoGain))

        # 如果当前的信息增益比原来的大
        if infoGain > bestInfoGain:
            # 最好的信息增益
            bestInfoGain = infoGain
            # 新的最好的用来划分的特征值
            bestFeature = i

            flagSeries = 0
            if not isinstance(dataSet[0][bestFeature], str):
                flagSeries = 1
                bestSeriesMid = bestMid

    # print('信息增益最大的特征为：' + labels[bestFeature])
    if flagSeries:
        return bestFeature, bestSeriesMid
    else:
        return bestFeature


def getDataSet(test_size):
    """
    创建测试的数据集，里面的数值中具有连续值
    :return:
    """
    dataSet = pd.read_csv("iris.data").values.tolist()
    random.shuffle(dataSet)
    train_dataset = dataSet[:int(len(dataSet) * (1 - test_size))]  # 训练数据
    test_dataset = dataSet[int(len(dataSet) * (1 - test_size)):]  # 测试数据
    # 特征值列表
    labels = ['sepal length', 'sepal width', 'petal length', 'petal width']

    return train_dataset, test_dataset, labels


def majorityCnt(classList):
    """
    找到次数最多的类别标签
    :param classList:
    :return:
    """
    # 用来统计标签的票数,更强得容器,默认为0
    classCount = collections.defaultdict(int)

    # 遍历所有的标签类别
    for vote in classList:
        classCount[vote] += 1

    # 从大到小排序
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)

    # 返回次数最多的标签
    return sortedClassCount[0][0]


def createTree(dataSet, labels):
    """
    创建决策树
    :param dataSet: 数据集
    :param labels: 特征标签
    :return:
    """
    # 拿到所有数据集的分类标签
    classList = [example[-1] for example in dataSet]

    # 统计第一个标签出现的次数，与总标签个数比较，如果相等则说明当前列表中全部都是一种标签，此时停止划分
    if classList.count(classList[0]) == len(classList):
        return classList[0]

    # 计算第一行有多少个数据，如果只有一个的话说明所有的特征属性都遍历完了，剩下的一个就是类别标签
    if len(dataSet[0]) == 1:
        # 返回剩下标签中出现次数较多的那个
        return majorityCnt(classList)

    # 选择最好的划分特征，得到该特征的下标
    bestFeat = chooseBestFeatureToSplit(dataSet=dataSet, labels=labels)

    # 得到最好特征的名称
    bestFeatLabel = ''

    # 记录此刻是连续值还是离散值,1连续，2离散
    flagSeries = 0

    # 如果是连续值，记录连续值的划分点
    midSeries = 0.0

    # 如果是元组的话，说明此时是连续值
    if isinstance(bestFeat, tuple):
        # 重新修改分叉点信息
        bestFeatLabel = str(labels[bestFeat[0]]) + '=' + str(bestFeat[1])
        # 得到当前的划分点
        midSeries = bestFeat[1]
        # 得到下标值
        bestFeat = bestFeat[0]
        # 连续值标志
        flagSeries = 1
    else: #如果不是连续值得话
        # 得到分叉点信息
        bestFeatLabel = labels[bestFeat]
        # 离散值标志
        flagSeries = 0

    # 使用一个字典来存储树结构，分叉处为划分的特征名称
    myTree = {bestFeatLabel: {}}

    # 得到当前特征标签的所有可能值
    featValues = [example[bestFeat] for example in dataSet]

    # 连续值处理
    if flagSeries:

        # 将连续值划分为不大于当前划分点和大于当前划分点两部分
        eltDataSet, gtDataSet = splitDataSetForSeries(dataSet, bestFeat, midSeries)
        # 得到剩下的特征标签
        subLabels = labels[:]
        # 递归处理小于划分点的子树
        subTree = createTree(eltDataSet, subLabels)
        myTree[bestFeatLabel]['小于'] = subTree

        # 递归处理大于当前划分点的子树
        subTree = createTree(gtDataSet, subLabels)
        myTree[bestFeatLabel]['大于'] = subTree

        return myTree

    # 离散值处理
    else:

        # 将本次划分的特征值从列表中删除掉
        del (labels[bestFeat])
        # 唯一化，去掉重复的特征值
        uniqueVals = set(featValues)
        # 遍历所有的特征值
        for value in uniqueVals:
            # 得到剩下的特征标签
            subLabels = labels[:]
            # 递归调用，将数据集中该特征等于当前特征值的所有数据划分到当前节点下，递归调用时需要先将当前的特征去除掉
            subTree = createTree(splitDataSet(dataSet=dataSet, axis=bestFeat, value=value), subLabels)
            # 将子树归到分叉处下
            myTree[bestFeatLabel][value] = subTree
        return myTree


# 输入三个变量（决策树，属性特征标签，测试的数据）
def classify(inputTree, featLables, testVec):
    firstStr = list(inputTree.keys())[0]
    secondDict = inputTree[firstStr]  # 树的分支，子集合Dict
    featIndex = featLables.index(firstStr[:firstStr.index('=')])  # 获取决策树第一层在featLables中的位置
    for key in secondDict.keys():
        if testVec[featIndex] > float(firstStr[firstStr.index('=') + 1:]):
            if type(secondDict['大于']).__name__ == 'dict':
                classLabel = classify(secondDict['大于'], featLables, testVec)
            else:
                classLabel = secondDict['大于']
            return classLabel
        else:
            if type(secondDict['小于']).__name__ == 'dict':
                classLabel = classify(secondDict['小于'], featLables, testVec)
            else:
                classLabel = secondDict['小于']
            return classLabel


# 保存决策树
def storeTree(inputTree, filename):
    import pickle
    fw = open(filename, 'wb')
    pickle.dump(inputTree, fw)
    fw.close()


# 读取决策树
def grabTree(filename):
    import pickle
    fr = open(filename, 'rb')
    return pickle.load(fr)


def calConfuMatrix(myTree, label, test_dataSet):
    matrix = {'Iris-setosa': {'Iris-setosa': 0, 'Iris-versicolor': 0},
              'Iris-versicolor': {'Iris-setosa': 0, 'Iris-versicolor': 0}}
    for example in test_dataSet:
        predict = classify(myTree, label, example)  # 对测试数据进行测试，predict为预测的分类
        actual = example[-1]  # actual 为实际的分类
        matrix[actual][predict] += 1  # 填充confusion matrix
    return matrix


# 准确度
def precision(classes, matrix):
    precisionDict = {'Iris-setosa': 0, 'Iris-versicolor': 0}
    all_predict_num = 0  # 例如存储当预测值为Iris-setosa时的所有情况数量
    for classItem in classes:
        true_predict_num = matrix[classItem][classItem]  # 准确预测数量
        all_predict_num = 0
        for temp_class_item in classes:
            all_predict_num += matrix[temp_class_item][classItem]
        precisionDict[classItem] = round(true_predict_num / all_predict_num, 5)
    return precisionDict

#准确率
def score(classes, matrix):
    all_num=0
    all_right=0
    for classItem in classes:
        all_right += matrix[classItem][classItem]  # 准确预测数量
        for temp_class_item in classes:
            all_num += matrix[temp_class_item][classItem]
    score = round(all_right / all_num, 5)
    return score

# 召回率
def recall(classes, matrix):
    recallDict = {'Iris-setosa': 0, 'Iris-versicolor': 0}
    for classItem in classes:
        true_predict_num = matrix[classItem][classItem]  # 准确预测数量
        all_predict_num = 0  # 例如存储当预测值为Iris-setosa时的所有情况数量
        for temp_class_item in classes:
            all_predict_num += matrix[classItem][temp_class_item]
        recallDict[classItem] = round(true_predict_num / all_predict_num, 5)
    return recallDict


# 展示结果
def showResult(precisionValue, recallValue, classes):
    print('\t\t\t\t', '精确率', '\t', '召回率','\t','F1值')
    for classItem in classes:
        print(classItem, '\t', precisionValue[classItem], '\t', recallValue[classItem],'\t',round((2*precisionValue[classItem]*recallValue[classItem])/(precisionValue[classItem]+recallValue[classItem]),5))


if __name__ == '__main__':
    """ 
    处理连续值时候的决策树
    """
    train_dataSet, test_dataSet, labels = getDataSet(0.5)
    temp_label = labels[:]  # 深拷贝
    myTree = createTree(train_dataSet, labels)
    storeTree(myTree, 'tree.txt')
    myTree = grabTree('tree.txt')
    print(myTree)
    treePlotter.createPlot(myTree)
    matrix = calConfuMatrix(myTree, temp_label, test_dataSet)  # confusion matrix
    classes = ['Iris-setosa', 'Iris-versicolor']  # 所有分类
    precisionValue = precision(classes, matrix)
    recallValue = recall(classes, matrix)
    score=score(classes,matrix)
    showResult(precisionValue, recallValue, classes)
    print("准确率为:%f"%score)

treePlotter.py

# @Time    : 2017/12/18 19:46
# @Author  : Leafage
# @File    : treePlotter.py
# @Software: PyCharm

import matplotlib.pylab as plt
import matplotlib

# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']

# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")

# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")

# 箭头样式
arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    绘制一个节点
    :param nodeTxt: 描述该节点的文本信息
    :param centerPt: 文本的坐标
    :param parentPt: 点的坐标，这里也是指父节点的坐标
    :param nodeType: 节点类型,分为叶子节点和决策节点
    :return:
    """
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    """
    获取叶节点的数目
    :param myTree:
    :return:
    """
    # 统计叶子节点的总数
    numLeafs = 0

    # 得到当前第一个key，也就是根节点
    firstStr = list(myTree.keys())[0]

    # 得到第一个key对应的内容
    secondDict = myTree[firstStr]

    # 递归遍历叶子节点
    for key in secondDict.keys():
        # 如果key对应的是一个字典，就递归调用
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        # 不是的话，说明此时是一个叶子节点
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    """
    得到数的深度层数
    :param myTree:
    :return:
    """
    # 用来保存最大层数
    maxDepth = 0

    # 得到根节点
    firstStr = list(myTree.keys())[0]

    # 得到key对应的内容
    secondDic = myTree[firstStr]

    # 遍历所有子节点
    for key in secondDic.keys():
        # 如果该节点是字典，就递归调用
        if type(secondDic[key]).__name__ == 'dict':
            # 子节点的深度加1
            thisDepth = 1 + getTreeDepth(secondDic[key])

        # 说明此时是叶子节点
        else:
            thisDepth = 1

        # 替换最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth

    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):
    """
    计算出父节点和子节点的中间位置，填充信息
    :param cntrPt: 子节点坐标
    :param parentPt: 父节点坐标
    :param txtString: 填充的文本信息
    :return:
    """
    # 计算x轴的中间位置
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    # 计算y轴的中间位置
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    # 进行绘制
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    """
    绘制出树的所有节点，递归绘制
    :param myTree: 树
    :param parentPt: 父节点的坐标
    :param nodeTxt: 节点的文本信息
    :return:
    """
    # 计算叶子节点数
    numLeafs = getNumLeafs(myTree=myTree)

    # 计算树的深度
    depth = getTreeDepth(myTree=myTree)

    # 得到根节点的信息内容
    firstStr = list(myTree.keys())[0]

    # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)

    # 绘制该节点与父节点的联系
    plotMidText(cntrPt, parentPt, nodeTxt)

    # 绘制该节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)

    # 得到当前根节点对应的子树
    secondDict = myTree[firstStr]

    # 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD

    # 循环遍历所有的key
    for key in secondDict.keys():
        # 如果当前的key是字典的话，代表还有子树，则递归遍历
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/W
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            # 打开注释可以观察叶子节点的坐标变化
            # print((plotTree.xOff, plotTree.yOff), secondDict[key])
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制叶子节点和父节点的中间连线内容
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))

    # 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD


def createPlot(inTree):
    """
    需要绘制的决策树
    :param inTree: 决策树字典
    :return:
    """
    # 创建一个图像
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 计算出决策树的总宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    # 计算出决策树的总深度
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2W
    plotTree.xOff = -0.5/plotTree.totalW
    # 初始的y轴偏移量，每次向下或者向上移动1/D
    plotTree.yOff = 1.0
    # 调用函数进行绘制节点图像
    plotTree(inTree, (0.5, 1.0), '')
    # 绘制
    plt.show()


if __name__ == '__main__':
    testTree = {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}, 3: 'maybe'}}
    createPlot(testTree)

结果：

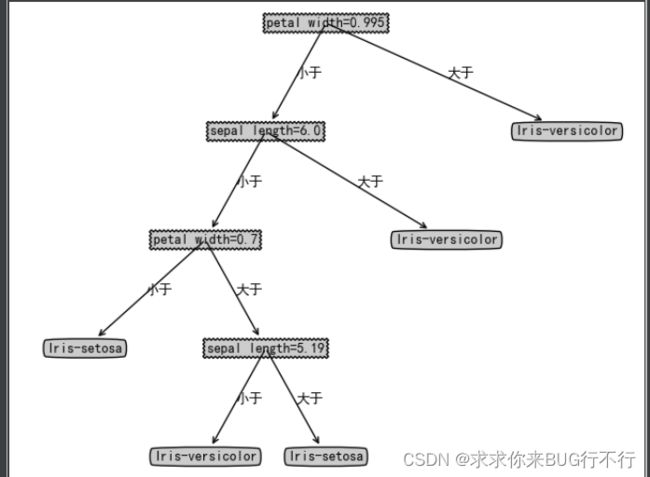
其他的自己慢慢测试即可。
本来还有SVM,逻辑斯蒂回归，贝叶斯对这个数据集的二分类，但一次吸收一点点即可，后面的陆续更新~

数据集就是可以通过sklearn库处理，如果需要txt数据集，私信我免费发送给你。
代码出处：
https://blog.csdn.net/kai123wen/article/details/105769970

https://github.com/login?return_to=%2Fjiajia0%2FMachineLearningTopic

KNN代码忘记出处了。
本人仅在读懂的基础上，然后通过修改参数以及代码变成自己想要的了。
一起加油吧！！！