Java数据结构与算法——线性表(list)
文章目录
- 一、线性表的定义
- 二、线性表的抽象数据类型
- 三、线性表的顺序存储结构及实现
-
-
- 1、顺序存储结构
- 2、插入数据
- 3、移除数据
- 4、数组长度与线性表长度的区别
- 5、顺序存储的优缺点
- 6、完整代码实现
-
- 四、线性表的链式存储结构及实现(单链表)
-
-
- 1、链式存储结构
- 2、链式存储结构存储示意图
- 3、单链表的读取
- 4、插入元素
- 5、删除元素
- 6、单链表的整表创建
- 7、完整代码
-
- 五、双向链表及实现
-
-
- 1、双向链表
- 2、代码实现
-
一、线性表的定义
线性表——零个或多个数据元素的有限序列。
注意:
首先它是一个序列。元素之间是有顺序的,若存在多个元素,则第一个元素无前驱,最后一个元素无后继,其他每个元素都有且只有一个前驱和后继。线性表的元素个数n定义为线性表的长度,当 n = 0 时,称为空表。
二、线性表的抽象数据类型
public interface ListADT {
public void clear();// 置空
public boolean isEmpty();// 判空
public int length();// 顺序表的长度
public Object get(int index) throws Exception;// 获取指定位置的元素
public void add(Object data);// 添加数据(添加至表尾)
public void insert(int index, Object data) throws Exception;// 指定位置插入数据
public void delete(int index) throws Exception;// 删除指定位置的元素
public int indexOf(Object data);// 返回给定数据的索引
public void display();// 遍历
}三、线性表的顺序存储结构及实现
1、顺序存储结构
用一段地址连续的存储单元依次存储线性表的数据元素(即用数组保存数据),也称顺序表。所有元素的存储位置取决于第一个元素的存储位置。
2、插入数据
(1)插入数据的三种情况:
- 线性表为空的情况——从 0 位置开始放就可以;
- 插入到末尾;
- 一般情况——腾出地方,然后插入;将要插入位置元素之后的元素往后移动一个位置。
(2)插入算法的思路:
- 如果插入位置不合理,抛出异常;
- 如果线性表长度大于数组长度,抛出异常或动态增加容量;
- 从最后一个元素开始向前遍历到第 i 个位置,分别将它们都向后移动一位;
- 将要插入的元素放到位置 i 处;
- 表长加 1。
3、移除数据
(1)移除数据的两种情况:
- 移除表尾的数据——直接置空;
- 一般情况——移除指定位置的数据,然后把后面的数据往前移动一个位置。
(2)移除元素算法的思路:
- 如果删除元素位置不合理,抛出异常;
- 取出删除元素;
- 从删除元素位置开始遍历到最后一个元素位置,分别将它们向前移动一位;
- 表长减1。
4、数组长度与线性表长度的区别
数组长度是存放线性表的存储空间的长度,线性表的长度是线性表中数据元素的个数。任意时刻,线性表的长度应该小于数组长度。
5、顺序存储的优缺点
优点:可以快速存取;
缺点:插入和删除操作需要移动大量元素;当线性表长度变化较大时,难以确定存储空间的容量;造成存储空间的“碎片”。
6、完整代码实现
public class SequenceList implements ListADT{
private int DEFAULT_SIZE = 5;// 数组的默认长度
private Object[] dataArray;
private int capacity;// 数组的长度
private int size = 0;// 顺序表的长度(保存顺序表当前数据的个数)
// 无参构造器:创建一个默认长度的空顺序表
public SequenceList(){
capacity = DEFAULT_SIZE;
dataArray = new Object[capacity];
}
// 有参构造器:用指定数据创建一个默认长度的顺序表
public SequenceList(Object data){
this();
dataArray[0] = data;
size++;
}
// 有参构造器:创建指定大小的顺序表
public SequenceList(Object data, int initSize){
capacity = initSize;
dataArray = new Object[capacity];
dataArray[0] = data;
size++;
}
@Override
// 置空
public void clear() {
Arrays.fill(dataArray, null);
size = 0;
}
@Override
// 判空
public boolean isEmpty() {
return size == 0;
}
@Override
// 返回顺序表的长度
public int length() {
return size;
}
@Override
// 获取指定位置的数据
public Object get(int index) throws Exception {
if(index < 0 || index > size){
throw new IndexOutOfBoundsException("第" + index +"个元素不存在");
}
return dataArray[index];
}
// 添加数据(添加至表尾)
public void add(Object data) {
// 顺序表已满,扩容
if(capacity == size){
expand();
}
dataArray[size] = data;
size++;
}
@Override
// 在指定位置插入数据
public void insert(int index, Object data) throws Exception {
// 顺序表已满,扩容
if(capacity == size){
expand();
}
if(index < 0 || index > size){
throw new IndexOutOfBoundsException("插入位置不合理!");
}
// 插入位置及之后的元素后移一位
for (int i = size; i > index; i--) {
dataArray[i] = dataArray[i - 1];
}
dataArray[index] = data;
size++;// 表长加一
}
// 扩容
private void expand(){
capacity = capacity * 2;
dataArray = Arrays.copyOf(dataArray, capacity);
}
@Override
// 删除指定位置的数据
public void delete(int index) throws Exception {
if(index < 0 || index > size){
throw new Exception("删除位置不合理!");
}
// 被删除数据之后的数据左移
for (int i = index; i < size; i++) {
dataArray[i] = dataArray[i + 1];
}
size--;
}
@Override
// 返回给定数据的索引
public int indexOf(Object data) {
int i = 0;
// 查找给定数据的位置
while(i < size && !dataArray[i].equals(data)){
i++;
}
if(i < size){
return i;
}else{
return -1;
}
}
@Override
public void display() {
if(isEmpty()){
System.out.println("顺序表为空!");
}else{
for (int i = 0; i < size; i++) {
System.out.print(dataArray[i] + " ");
}
System.out.println();
}
}
}四、线性表的链式存储结构及实现(单链表)
1、链式存储结构
用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。在链式结构中,除了要存储数据元素外,还要存储它的后继元素的存储地址。
为了表示数据元素 a i a_i ai 与其直接后继数据元素 a i + 1 a_{i+1} ai+1 之间的逻辑关系,对数据元素 a i a_i ai 来说,除了存储其本身的信息之外,还需要存储一个指示其直接后继的信息(即直接后继的存储位置信息)。把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称作指针或链。这两部分信息组成数据据元素 a i a_i ai 的存储映像,称为结点。
n 个结点链结成一个链表,即为线性表的链式存储结构,因为此链表的每个结点只包含一个指针域,又叫单链表。如图:

链表中第一个结点的存储位置叫做头指针。最后一个结点没有直接后继,规定最后一个结点指针为“空”。

为了方便操作,会在单链表的第一个结点之前附设一个节点,称为头结点。头结点的数据域可以不存储信息,也可以存储线性表的长度信息,头结点的指针域存储指向第一个结点的指针。
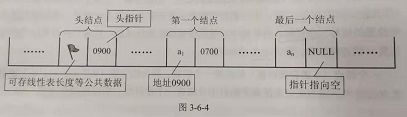
头指针和头结点的异同:
头指针:
- 头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针;
- 头指针具有标识作用,常用头指针冠以链表的名字;
- 无论链表是否为空,头指针均不为空,头指针是链表的必要元素。
头结点:
- 头结点是为了操作方便而设立的,放在第一个元素的结点之前,其数据域一般无意义;
- 有了头结点,对在第一元素结点前插入元素和删除第一结点,其操作和其他结点的操作一样;
- 头结点不一定是链表必须元素。
2、链式存储结构存储示意图

结点由存放数据元素的数据域和存放后继结点地址的指针域组成。如图:

3、单链表的读取
读取第 i 个元素,必须从头开始找。算法思路:
- 声明一个指针 p 指向链表的第一个结点,初始化 j 从1开始;
- 当 j < i 时,就遍历链表,让 p 的指针向后移动,不断地指向下一个结点,j 累加1;
- 若移动到链表末尾 p 为空,则说明第 i 个结点不存在;
- 否则查找成功,返回结点 p 的数据。
但是,由于链表的结构中没有定义表长,所以事先不知道要循环多少次,因此不方便使用 for 循环实现。其核心思想是“工作指针后移”。
4、插入元素
假设存储元素 e 的结点为 s,将结点 s 插入到结点 p 和 p->next之间,只需改变 s->next 和 p->next 的指针,即把 p 的后继结点改成 s 的后继结点,再把结点 s 变成 p 的后继结点。如下图:

代码如下:
s->next = p->next;
p->next = s;
注意: 两行代码的顺序不能交换。
算法思路:
- 声明一个指针 p 指向链表头结点,初始化 j 从 1 开始;
- 当 j < i 时,就遍历链表,让 p 的指针向后移动,不断指向下一个结点,j 累加 1;
- 若到链表末尾 p 为空,则说明第 i 个结点不存在;
- 否则查找成功,在系统中生成一个空结点 s;将数据元素 e 赋值给s->data;
- 单链表的插入标准语句:s->next = p->next;p->next = s;
- 返回成功。
5、删除元素
假设 q 是 p 的直接后继结点,删除结点 q,就是把 p 的后继结点改成 p 的后继的后继结点。即 p.next = p.next.next;
算法思路:
- 声明一个指针 p 指向链表头结点;
- 遍历链表,让 p 的指针向后移动,不断指向下一个结点,直至要删除结点的前驱;
- 若到链表末尾 p 为空,则说明要删除的元素不存在;
- 否则成功找到要删除的元素;
- 删除元素标准语句:p.next = p.next.next;
6、单链表的整表创建
链表所占用空间的大小和位置不需要预先分配,可以即时生成,其创建过程就是一个动态生成链表的过程,即从“空表”的初始状态起,依次建立各元素结点,并逐个插入链表。
算法思路(头插法):
- 声明一个指针 p 和计数器变量 i;
- 初始化一个空链表 L;
- 让 L 的头结点的指针指向null,即建立一个带头结点的单链表;
- 循环:生成一个新结点赋值给 p,随机生成一数字赋值给 p 的数据域 p->data,将 p 插入到头结点与前一个新结点之间。
还可以使用尾插法,需要注意:要始终让 r 指向尾结点,并且在循环结束后还应该让这个结点的指针域置空。
7、完整代码
抽象数据类型:
public interface LinkListADT<T> {
public boolean isEmpty();
public int size();
public void clear();
public T get(int index);
public void add(T element); //添加元素,默认尾部添加
public void addFirst(T element);
public void addLast(T element);
public void add(int index, T element);
public void remove(T element);
public void display();
}单链表代码实现:
public class LinkList<T> implements LinkListADT<T>{
// 内部类,节点类
private class Node{
public Object data;// 数据域
public Node next;// 指针域
public Node(){}
public Node(Object data, Node next) {
this.data = data;
this.next = next;
}
}
private Node head;// 头结点
private Node tail;// 尾结点
private int size;// 保存已有的结点数
// 创建空链表
public LinkList(){
head = null;
tail = null;
}
// 以指定元素创建链表,只含一个元素
public LinkList(T element){
head = new Node(element, null);
tail = head;// //只有一个结点,header和tail都指向该结点
size++;
}
@Override
// 判空
public boolean isEmpty() {
return size == 0;
}
@Override
// 链表的大小
public int size() {
return size;
}
@Override
// 置空
public void clear() {
head = null;
tail = null;
size = 0;
}
@Override
// 获取元素
public T get(int index) {
if(index < 0 || index > size){
throw new IndexOutOfBoundsException("Index out of bound!");
}
Node p = head;
int count = 1;
while(p != null && count < index){
p = p.next;
count++;
}
if(p == null || count > size){
System.out.println("第" + index + "个元素不存在!");
}
return (T)p.data;
}
@Override
// 添加元素(默认添加至表尾)
public void add(T element) {
addLast(element);
}
@Override
// 链表头部插入元素(头插法)
public void addFirst(T element) {
Node node = new Node(element, null);
node.next = head;
head = node;
// 若插入前是空表
if(tail == null){
tail = head;
}
size++;
}
@Override
// 链表尾部添加元素,要先判断是否为空表,
public void addLast(T element) {
// 如果链表为空,那么头指针还是null,所以处理一下头指针
if(head == null){
head = new Node(element, null);
tail = head;// 这样处理之后,head和tial都指向同一个节点
}else{
Node node = new Node(element, null);
tail.next = node;
tail = node;// tail重新指向尾结点
}
size++;
}
@Override
// 指定位置添加元素
public void add(int index, T element) {
int count = 1;
Node p = head;
Node s = new Node();// 给要插入的元素创建节点
while(p != null && count < index){
p = p.next;
count++;
}
if(p == null || count > index){
System.out.println("不能插入!");
}
s.data = element;
s.next = p.next;
p.next = s;
size++;
}
@Override
// 移除元素
public void remove(T element) {
Node p = head;
// 注意:要使p指向要删除元素对应结点的前一个结点
while(p != null && !p.next.data.equals(element)){
p = p.next;
}
if(p == null){
System.out.println("元素不存在!");
}
p.next = p.next.next;
}
@Override
// 遍历
public void display() {
Node node = head;
while(node != null){
System.out.print(node.data + " ");
node = node.next;
}
System.out.println();
}
}五、双向链表及实现
1、双向链表
每个结点包含一个数据域和两个指针域,两个指针域分别保存对下一个结点和前一个结点的引用。
2、代码实现
public class DoubleLinkList {
// 节点类
private class Node{
public Object data;// 数据域
public Node next;// 后继指针域
public Node pre;// 前驱指针域
public Node(){
this.next = null;
this.pre = null;
}
public Node(Object data){
this();
this.data = data;
}
}
private Node head;// 头结点
private Node tail;// 尾结点
private int size = 0;// 保存已有的结点数
public DoubleLinkList(){
head = null;
tail = null;
}
// 判空
public boolean isEmpty(){
return size == 0;
}
// 链表头部添加结点
public void addHead(Object data){
Node node = new Node(data);// 为要添加的数据创建一个新结点
if(head == null){// 链表为空,设置尾结点为新添加的结点
tail = node;
}else{
head.pre = node;// 新结点作为当前头结点的前驱
node.next = head;// 当前头结点作为新结点的后继
}
head = node;
size++;
}
// 删除头结点
public void deleteHead(){
if(isEmpty()){
System.out.println("链表为空!");
}else{
Node node = head;
head = node.next;
head.pre = null;
}
size--;
}
// 链表尾部添加结点
public void addTail(Object data){
Node node = new Node(data);
if(head == null){
head = node;
}else{
tail.next = node;
node.pre = tail;
}
tail = node;
size++;
}
// 删除尾结点
public void deleteTail(){
if(isEmpty()){
System.out.println("链表为空!");
}
else{
Node node = tail;
tail = node.pre;
tail.next = null;
}
size--;
}
// 查找(根据数据域查找)
public Node find(Object data){
Node node = head;
while(!node.data.equals(data)){
if(node.next == null){// 遍历至表尾仍为空,返回null
return null;
}
node = node.next;
}
return node;
}
// 删除(根据数据域删除)
public Node delete(Object data){
Node node = head;
while(!node.data.equals(data)){
if(node.next == null){// 遍历至表尾仍为空,返回null
return null;
}
node = node.next;
}
if(node == head){
head = node.next;
}else{
node.pre.next = node.next;
}
return node;
}
// 遍历
public void display(){
Node node = head;
while(node != null){
System.out.print(node.data + " ");
node = node.next;
}
System.out.println();
}
public static void main(String[] args) {
DoubleLinkList list = new DoubleLinkList();
list.addHead(1);
list.addHead(2);
list.addHead(3);
list.addTail(4);
list.addTail(5);
list.addTail(6);
list.display();
list.deleteHead();
list.display();
list.deleteTail();
list.display();
list.delete(4);
list.display();
}
}运行结果:
3 2 1 4 5 6
2 1 4 5 6
2 1 4 5
2 1 5