【Leetcode】刷题之路3（python版）

回溯专题

1.回溯算法的本质是n叉树的深度优先搜索，同时，需要注意剪枝减少复杂度。

2.回溯算法三部曲

• 确定参数和返回值
• 回溯函数终止条件
• 单层循环

3.回溯法思路
回溯法是一种算法思想，而递归是一种编程方法，回溯法可以用递归来实现。

回溯法的整体思路是：搜索每一条路，每次回溯是对具体的一条路径而言的。对当前搜索路径下的的未探索区域进行搜索，则可能有两种情况：

• 当前未搜索区域满足结束条件，则保存当前路径并退出当前搜索；
• 当前未搜索区域需要继续搜索，则遍历当前所有可能的选择：如果该选择符合要求，则把当前选择加入当前的搜索路径中，并继续搜索新的未探索区域。

4.回溯算法模版（python版）

在递归调用之前「做选择」，在递归调用之后「撤销选择」

def backtrack(params){
       if 终止条件:
            存放结果；
            return;
        }
        for 遍历：本层n叉树的元素:
            处理节点；(需要剪枝)
            backtrack(params，选择列表);
            撤销操作；
        }    
}

回溯法搜所有可行解的模板一般是这样的：

res = []
path = []

def backtrack(未探索区域, res, path):
    if 未探索区域满足结束条件:
        res.add(path) # 深度拷贝
        return
    for 选择 in 未探索区域当前可能的选择:
        if 当前选择符合要求:
            path.add(当前选择)
            backtrack(新的未探索区域, res, path)
            path.pop()

重点概括：

• 如果解决一个问题有多个步骤，每一个步骤有多种方法，题目又要我们找出所有的方法，可以使用回溯算法；
• 回溯算法是在一棵树上的 深度优先遍历（因为要找所有的解，所以需要遍历），按选优条件向前搜索，以达到目标，但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法。回溯算法首先需要画出递归树，不同的树决定了不同的代码实现。

4.回溯算法解决的问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 棋盘问题：N皇后，解数独等等

组合问题

• 77. 组合
• 39. 组合总和
• 40. 组合总和II
• 216. 组合总和III
• 17. 电话号码的字母组合

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。

题解

组合问题，相对于排列问题而言，不计较一个组合内元素的顺序性（即 [1, 2, 3] 与 [1, 3, 2] 认为是同一个组合），因此很多时候需要按某种顺序展开搜索，这样才能做到不重不漏。

把组合问题抽象为如下树形结构：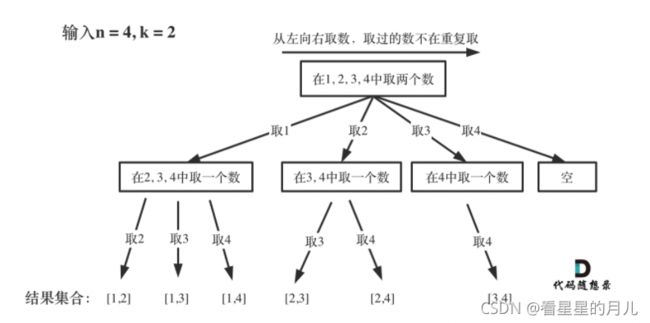
可以看出这个棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。

根据三部曲：
（1）递归函数的参数和返回值
函数里一定有两个参数，既然是集合n里面取k的数，那么n和k是两个int型的参数。然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,…,n] ）。

（2）终止条件
path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在树中path存的就是根节点到叶子节点的路径。

（3）单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程，可以for循环用来横向遍历，递归的过程是纵向遍历。
for循环每次从startIndex开始遍历，然后用path保存取到的节点。

剪枝优化：
举一个，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。如图所示：

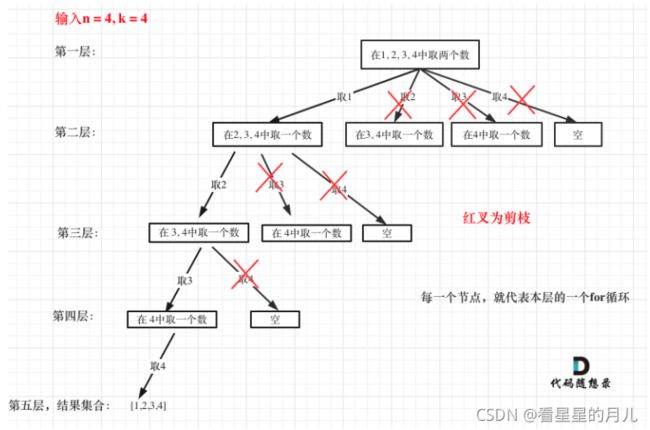
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。
所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了

优化过程：
接下来看一下优化过程如下：

• 已经选择的元素个数：path.size();
• 还需要的元素个数为: k - path.size();
• 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历（+1是因为包括起始位置，我们要是一个左闭的集合。）

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        res=[]  #存放符合条件结果的集合
        path=[]  #用来存放符合条件结果
        def backtrack(n,k,startIndex):
            if len(path) == k:
                res.append(path[:])
                return 
            for i in range(startIndex,n-(k-len(path))+2):  #优化的地方
                path.append(i)  #处理节点 
                backtrack(n,k,i+1)  #递归
                path.pop()  #回溯，撤销处理的节点
        backtrack(n,k,1)
        return res

39. 组合总和

给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。
对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

题解

思路分析：

根据示例 1：输入: candidates = [2, 3, 6, 7]，target = 7。
候选数组里有 2，如果找到了组合总和为 7 - 2 = 5 的所有组合，再在之前加上 2 ，就是 7 的所有组合；
同理考虑 3，如果找到了组合总和为 7 - 3 = 4 的所有组合，再在之前加上 3 ，就是 7 的所有组合，依次这样找下去。

变量意义：use表示已经使用过的数（组成的列表），remain表示距离target还有多大。

对candidates升序排序，以方便根据remain的大小使用return减小搜索空间；
递归求可能的组合。具体的，每次递归时对所有candidates做一次遍历，情况有三种：
1，满足条件，则答案加入一条；
2，不足，继续递归；
3，超出，则直接退出本路线。
注意每层递归都对全体candidates做遍历会导致如[2,2,3],[3,2,2]这样的对称重复的答案的产生。这是因为发生了 往前选择 的情况，我们每次更深层的递归都往后缩小一个candidates，强制函数只能 往后选择 ，这将不会出现重复答案。

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates = sorted(candidates)

        ans = []

        def find(s, use, remain):
            for i in range(s, len(candidates)):
                c = candidates[i]
                if c == remain:
                    ans.append(use + [c])
                    return
                if c < remain:
                    find(i, use + [c], remain - c)
                if c > remain:
                    return
        find(0, [], target)

        return ans

还有一种标准写法：

from typing import List

# 给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
# candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。 
# 对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

class Solution:
    def combinationSum(candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        res=[]  #存放符合条件结果的集合
        path=[]  #用来存放符合条件结果
        def backtrack(cur,startIndex):
            if cur > target: return  #剪枝操作
            if cur == target :  
                return res.append(path[:])
            for i in range(startIndex,len(candidates)):
                # if i > startIndex and candidates[i] == candidates[i - 1]:
                #     continue
                c = candidates[i]
                path.append(c)
                backtrack(cur+c,i) #i强制从自己开始往后选择
                path.pop()  #回溯
        backtrack(0,0)
        print(res)
        return res

40. 组合总和II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

题解

思路：
和 39. 组合总和 差不多，有以下两点不同：
1.数组candidates有重复数字；
2.数组中的数字不可重复使用
为了避免产生重复解，本题candidates务必排序

backtrack步骤如下：
剪枝：

• 如果当前tmp数组的和cur已经大于目标target，没必要枚举了，直接return
• 如果当前tmp数组的和cur正好和目标target相等，找到一个组合，加到结果res中去，并return
• for循环遍历从index开始的数，选一个数进入下一层递归。
  • 如果从index开始的数有连续出现的重复数字，跳过该数字continue，因为这会产生重复解
  • 因为数不可以重复选择，所以在进入下一层递归时，i要加1，从i之后的数中选择接下来的数

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        res = []
        n = len(candidates)
        candidates.sort()
        
        def backtrack(tmp, cur, index):
            if cur > target:
                return
            if cur == target:
                res.append(tmp)
                return
            for i in range(index, n):
                if i > index and candidates[i] == candidates[i - 1]:
                    continue
                backtrack(tmp + [candidates[i]], cur + candidates[i], i + 1)
        
        backtrack([], 0, 0)
        return res

标准模版写法：

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        res=[]  #存放符合条件结果的集合
        path=[]  #用来存放符合条件结果
        def backtrack(cur,startIndex):
            if cur > target: return  #剪枝操作
            if cur == target :  
                return res.append(path[:])
            for i in range(startIndex,len(candidates)):
                if i > startIndex and candidates[i] == candidates[i - 1]:
                    continue
                c = candidates[i]
                path.append(c)
                backtrack(cur+c,i+1)
                path.pop()  #回溯
        backtrack(0,0)

        return res

216. 组合总和III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：
所有数字都是正整数。
解集不能包含重复的组合。

题解

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        res = []  #存放结果集
        path = []  #符合条件的结果
        def findallPath(n,k,sum,startIndex):
            if sum > n: return  #剪枝操作
            if sum == n and len(path) == k:  #如果path.size() == k 但sum != n 直接返回
                return res.append(path[:])
            for i in range(startIndex,9-(k-len(path))+2):  #剪枝操作
                path.append(i)
                sum += i 
                findallPath(n,k,sum,i+1)  #注意i+1调整startIndex
                sum -= i  #回溯
                path.pop()  #回溯
        
        findallPath(n,k,0,1)
        return res

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例：
输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

题解

首先使用哈希表存储每个数字对应的所有可能的字母，然后进行回溯操作。

回溯过程中维护一个字符串，表示已有的字母排列（如果未遍历完电话号码的所有数字，则已有的字母排列是不完整的）。该字符串初始为空。每次取电话号码的一位数字，从哈希表中获得该数字对应的所有可能的字母，并将其中的一个字母插入到已有的字母排列后面，然后继续处理电话号码的后一位数字，直到处理完电话号码中的所有数字，即得到一个完整的字母排列。然后进行回退操作，遍历其余的字母排列。

回溯算法用于寻找所有的可行解，如果发现一个解不可行，则会舍弃不可行的解。在这道题中，由于每个数字对应的每个字母都可能进入字母组合，因此不存在不可行的解，直接穷举所有的解即可。

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return list()
        
        phoneMap = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz",
        }
        comb = list()
        res = list()
        def backtrack(index: int):
            if index == len(digits):
                res.append("".join(comb)) #转化成字符串
                return
            else:
                digit = digits[index]
                for letter in phoneMap[digit]:
                    comb.append(letter)
                    backtrack(index + 1)
                    comb.pop()
                   
        backtrack(0)
        return res

一行python代码，用iterator

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return list()
        
        phoneMap = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz",
        }

        groups = (phoneMap[digit] for digit in digits)
        return ["".join(combination) for combination in itertools.product(*groups)]