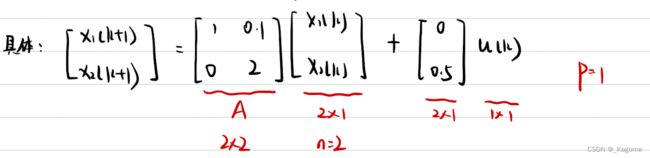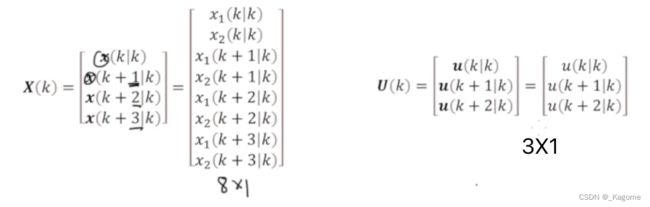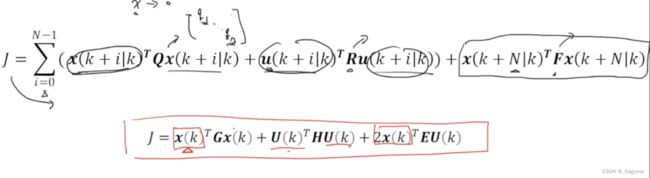MPC模型预测控制数学推导以及MatLab实现
文章目录
- 最优化控制
-
- SISO系统
- MIMO系统
- MPC基本概念
-
- 滚动优化
- 最优化建模
-
- 二次规划
- MPC建模
-
- 各向量维度
- 代码实现
最优化控制
研究动机:在一定的约束条件下达到最优的系统表现。
关于最优的,举个车变道的例子,从表面上来看,轨迹1行车轨迹很平滑,很舒适,没有什么急转弯;轨迹2是快速的,但是假如前面有了障碍物,也需要一种快速的紧急避障能力,所以关于最优的,还得分析特定的情况。
SISO系统
轨迹跟踪的性能表示: ∫ 0 t exp ( 2 ) d t \int_{0}^{t} \exp(2)\, dt ∫0texp(2)dt–>其结果越小,追踪的就越好。
(关于为什么采用 e x p ( 2 ) exp(2) exp(2)的解释:误差有正有负, e x p ( 2 ) exp(2) exp(2)可以把正负误差都统计上,外加绝对值也是可行的。至于为什么是积分结果越小,追踪的就好的解释:控制器在变化,看哪个控制器的误差积分最小,哪个控制器最优)
输入: ∫ 0 t u 2 d t \int_{0}^{t} \ u^2\, dt ∫0t u2dt->积分结果越小,输入越小。
物理条件:能耗最低的,可以用很小的能耗达到所需条件。
所以可以构建一个Cost Function,如 J = ∫ 0 t q e 2 + r u 2 d t J = \int_{0}^{t} \ {qe}^2+{ru}^2\, dt J=∫0t qe2+ru2dt。LQR控制
最优化的过程就是对 u u u进行设计,使得 m i n ( J ) min(J) min(J)。
q > > r q >> r q>>r:则说明更看重误差
r > > q r >> q r>>q:则说明更看重输入
MIMO系统
公式太难打了,看我手写图吧。

需要注意的是,上方我写的符号冲突了, y 1 − r 1 y_{1} - r_{1} y1−r1当中的 r 1 r_{1} r1是参考值( r 2 r_{2} r2同理),看上方的控制框图中的 r r r。而下方的 u T R u u^{T}Ru uTRu中的 r 1 , r 2 r_{1},r_{2} r1,r2是调节参数。
MPC基本概念
通过模型来预测系统在某一未来时间段内的表现来进行优化控制,多用于数位控制。
常用的是离散形式的表达式: X k + 1 = A X k + B u k X_{k+1} = AX_{k} + Bu_{k} Xk+1=AXk+Buk
MPC的步骤主要有三步:
在k时刻:
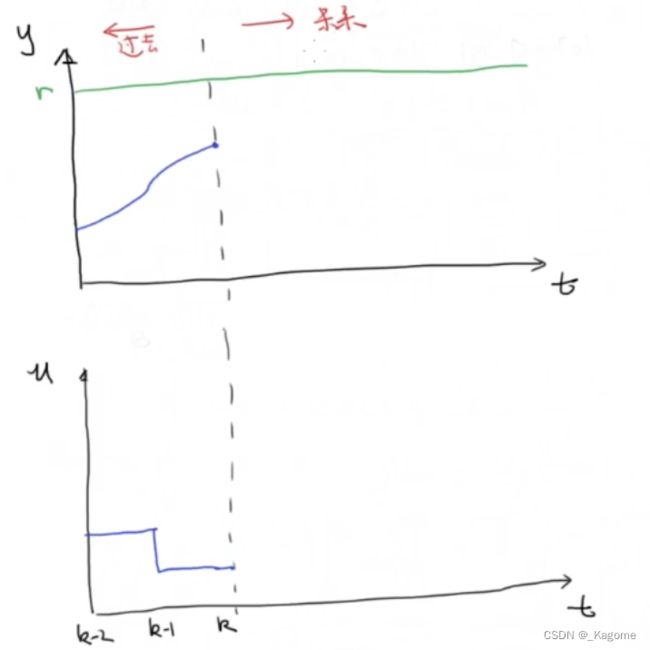
Step1:估计/测量读取当前系统状态: y k y_k yk
下图中的参数,分别是输入 u u u以及输出 y y y, r r r是其参考值。
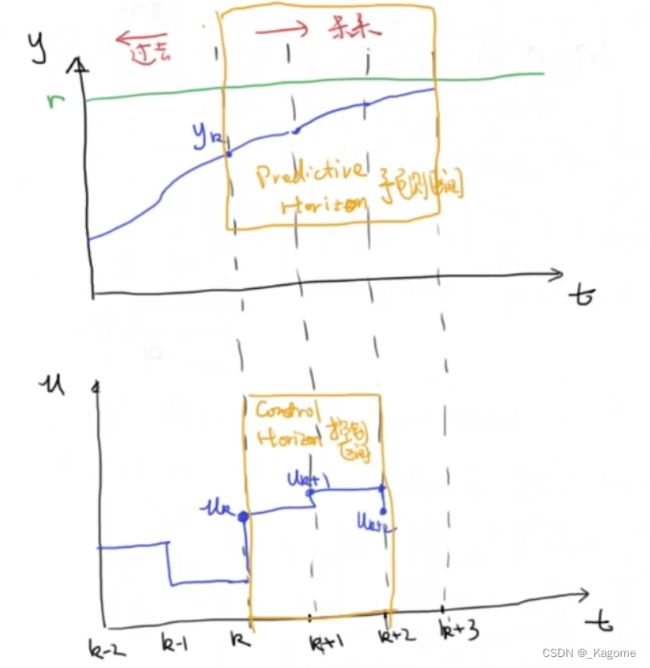
Step2:基于 u k , u k + 1 . . . . . . u k + N u_k,u_{k+1}......u_{k+N} uk,uk+1......uk+N来进行最优化
可以看出,下方当中的控制区间当中 u k u_k uk等参数的选择,就是一个最优化的过程。
其Cost Function就是如下:
J = ∑ k N − 1 E k T Q E K + u k T R u k + E N T F E N J = \sum\limits_{k}\limits^{N-1}{E_{k}^TQE_{K}+u_{k}^TRu_{k}+E_{N}^TFE_{N}} J=k∑N−1EkTQEK+ukTRuk+ENTFEN
其中最后一项, E N T F E N E_{N}^TFE_{N} ENTFEN代表的是最终时刻的最末一点误差的代价函数。
要做的就是把代价函数最优化找到它的最小值。
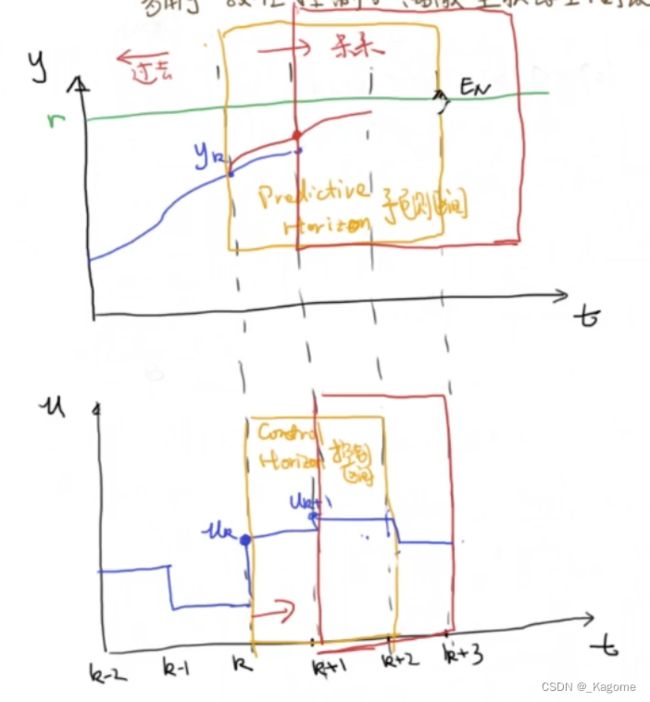
Step3:这一步是最关键的,上方说过了基于 u k , u k + 1 . . . . . . u k + N u_k,u_{k+1}......u_{k+N} uk,uk+1......uk+N来进行最优化,但是在MPC当中,算了这么多,只取 u k u_k uk,看N步走一步的思想,这是因为预测的模型很难完美描述现实当中的系统,在现实当中的系统可能会有扰动。那是不是之前的计算就白算了呢?没有白算,若不计算后面的 u k + 1 u_{k+1} uk+1之类的项目,就无法保证 k k k时刻能达到最优。
例如,你预测的是蓝色线段,但是实际的可能是蓝色线段上方的一个红色线段,有扰动。

滚动优化
进行刚刚的一个轮回选择完 u k u_k uk进行优化后,就是在发现实际有偏差之后,以当前的实际为基础,把之前整个黄色框图整体向未来移动一步,再进行优化设计(之前预测的蓝色线段就不要了)。
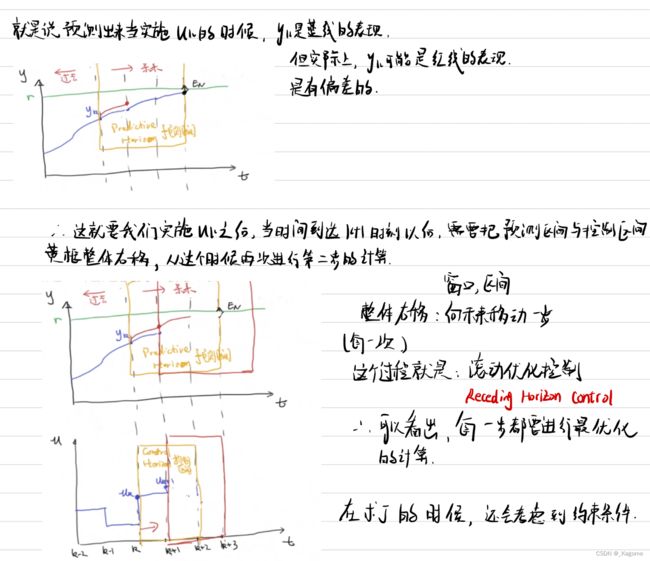
所以MPC对计算性能有要求,因为每一步都要进行最优化的计算。
最优化建模
以下公式太多,采用手写笔记替代,必要时会进行文字说明。
二次规划
因为二次规划的求解已经非常成熟了(MatLab/Python),所以可以把模型化成这样的一般形式,这样的话就可以扔到里面进行计算了。
关于为什么是 u k + N − 1 u_{k+N-1} uk+N−1而 x k + N x_{k+N} xk+N等维度不一致的问题,因为 x k + N x_{k+N} xk+N是由 u k + N − 1 u_{k+N-1} uk+N−1推出来的,所以少了一个。

记住这个绿色的 X k X_k Xk以及蓝色的 u k u_k uk。
就是将初始条件代入 A X + B U AX+BU AX+BU的方程中,计算出下一时刻后,就把新的时刻值再代入到之前的方程,再计算出下一时刻。反复计算,直到计算出 X ( k + N ∣ k ) {X}(k+N|k) X(k+N∣k),预测空间结束。
得到了绿色的 X k = M x k + C u k X_k = Mx_k + Cu_k Xk=Mxk+Cuk,把这个公式代入到下图当中的 J J J中进行化简。
记住,这里的 Q , R Q,R Q,R都是对角矩阵。

因为 J J J是一个数, 1 ∗ 1 1*1 1∗1的形式,所以中间两项转置也就是本身,可以进行合并。
就是说J是1乘1的矩阵,它的这几个分式子也只能是1乘1的加起来才是1乘1的,所以转置前后相等。
算了这么久,得到了新的代价函数: J = x k T G x k + 2 x k T E u k + u k T H u k J=x_k^TGx_k+2x_k^TEu_k+u_k^THu_k J=xkTGxk+2xkTEuk+ukTHuk,最开始的一项只是初始状态,对最优化部分不影响,有了模型后就能进行模型预测控制部分了。
二次规划的一般形式为: m i n z T Q z + c T z min z^TQz+c^Tz minzTQz+cTz
与二次规划的一般形式进行对比,发现是一模一样的
MPC建模
各向量维度
维度的问题需要清楚的了解。
X k X_k Xk维度: ( N + 1 ) n ∗ 1 (N+1)n*1 (N+1)n∗1
U k U_k Uk维度: N p ∗ 1 Np*1 Np∗1

M M M的维度: ( N + 1 ) n ∗ n (N+1)n*n (N+1)n∗n
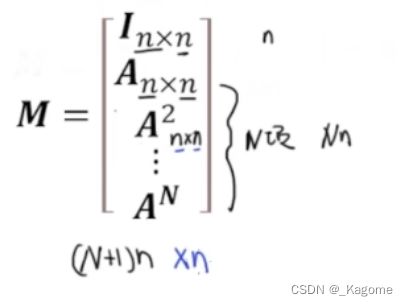
C C C的维度: ( N + 1 ) n ∗ N p (N+1)n*Np (N+1)n∗Np
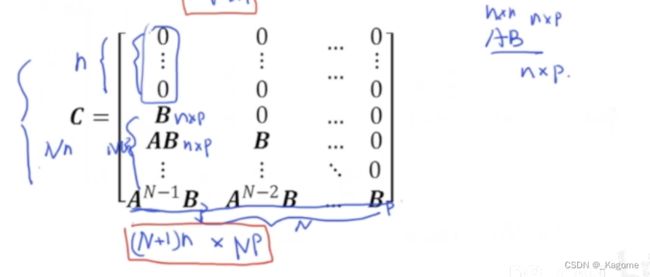
之前最优化建模当中推得的表达式为: X ( k ) = M x ( k ) + C U ( k ) X(k)=Mx(k)+CU(k) X(k)=Mx(k)+CU(k)

接下来,就用SISO的例子,具体算一下。
现在只包含了输入项以及初始状态项,所以对其进行最优化,就能得到输入的一个最优化结果了。以上是非常关键的一点。
代码实现
%% 清屏
clear;
close all;
clc;
%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 第一步,定义状态空间矩阵
%% 定义状态矩阵 A, n x n 矩阵
A = [1 0.1; -1 2];
n= size (A,1);
%% 定义输入矩阵 B, n x p 矩阵
B = [ 0.2 1; 0.5 2];
p = size(B,2);
%% 定义Q矩阵,n x n 矩阵
Q=[100 0;0 1];
%% 定义F矩阵,n x n 矩阵
F=[100 0;0 1];
%% 定义R矩阵,p x p 矩阵
R=[1 0 ;0 .1];
%% 定义step数量k
k_steps=100;
%% 定义矩阵 X_K, n x k 矩 阵
X_K = zeros(n,k_steps);
%% 初始状态变量值, n x 1 向量
X_K(:,1) =[20;-20];
%% 定义输入矩阵 U_K, p x k 矩阵
U_K=zeros(p,k_steps);
%% 定义预测区间K
N=5;
%% Call MPC_Matrices 函数 求得 E,H矩阵
[E,H]=MPC_Matrices(A,B,Q,R,F,N);
%% 计算每一步的状态变量的值
for k = 1 : k_steps
%% 求得U_K(:,k)
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);
%% 计算第k+1步时状态变量的值
X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));
end
%% 绘制状态变量和输入的变化
subplot (2, 1, 1);
hold;
for i =1 :size (X_K,1)
plot (X_K(i,:));
end
legend("x1","x2")
hold off;
subplot (2, 1, 2);
hold;
for i =1 : size (U_K,1)
plot (U_K(i,:));
end
legend("u1","u2")
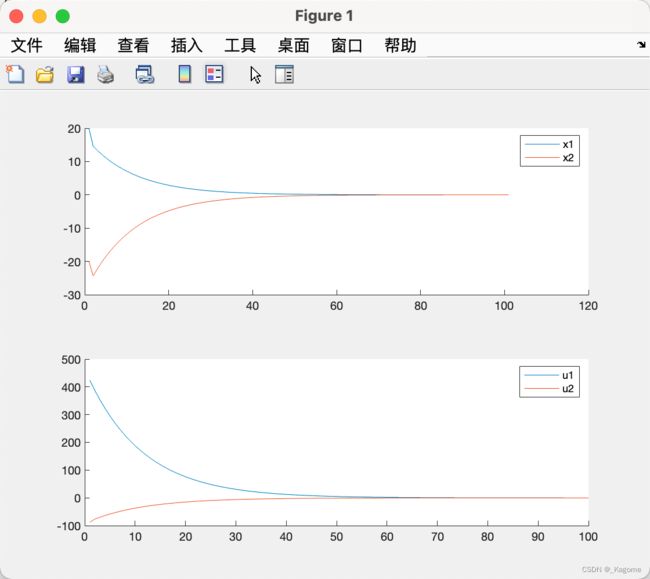
可以看出随着K的增加,是逐渐趋向于0的。要侧重于 x 1 , x 2 , u 1 , u 2 x_1,x_2,u_1,u_2 x1,x2,u1,u2可以修改代码当中对应的权重系数。
以上不光适用于SISO,也适用于MIMO。