【Python数据结构与算法】（六）排序算法（下）：快速、归并、计数

【Python数据结构与算法】（六）排序算法（下）：快速、归并、计数

• ✨本文收录于《Python数据结构与算法》专栏，此专栏主要记录如何python学习数据结构与算法笔记。
• 个人主页：JoJo的数据分析历险记
• 个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 如果文章对你有帮助，欢迎✌关注、点赞、✌收藏、订阅专栏

排序算法下：归并排序、快速排序、记数排序

上一章我们介绍了几个基础排序算法，但是他们的运行效率比较低，下面我们介绍几种比较快的排序算法。

1.快速排序

1.1基本思想

快速排序（Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

具体思路如下：

• 取一个元素p，称为"基准"（pivot），使其归位
• 列表被p分成两个部分，其中，左边的都比p小，右边的都比p大
• 递归完成两边的元素进行排序

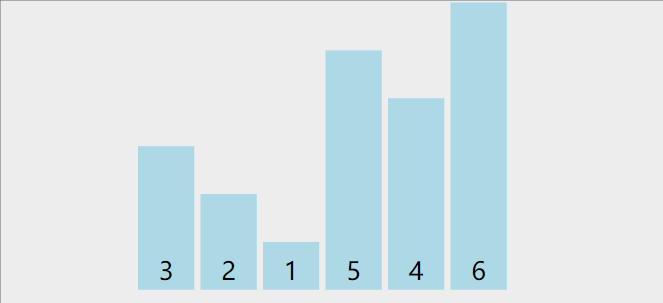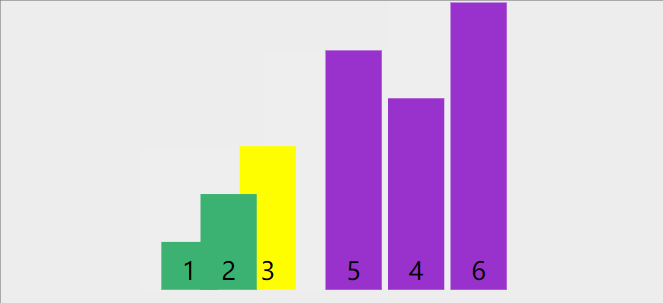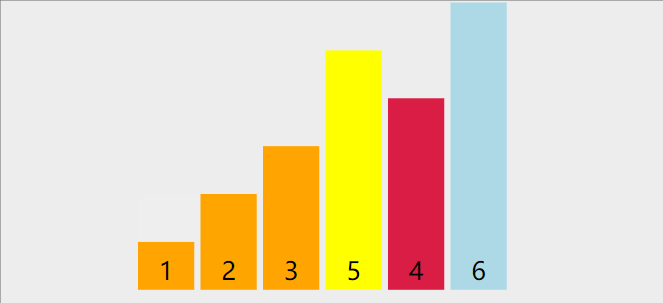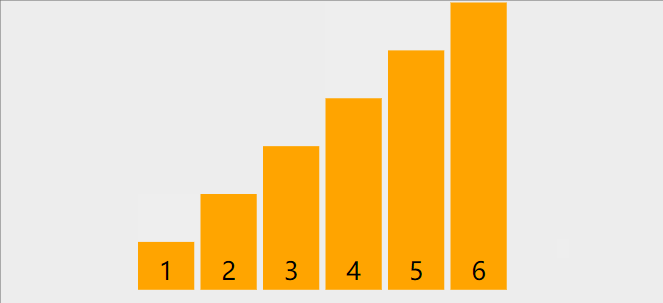
以下图为例

首先，将第一个数3作为基数，然后定义两个指针left和right,然后从右边找到比3小的数，找到后，让li[left] = li[right],然后再从左往右，找到比3大的数字，然后让li[right]=li[left],指导left和right重合为止。

1.2代码实现

下面我们来看一下具体的代码实现

# 首先定义分区函数
def partition(li,left,right):
    tmp = li[left]#存储最左边的数
    while left < right:
        """从右往左找"""
        while left < right and li[right] >= tmp:#从右边找到比tmp小的数字
            right -= 1 #指针向左移动
        li[left] = li[right]#跳出循环后，让li[left] = li[right]
        """从左往右找"""
        while left<right and li[left] <= tmp:#从左边找出比tmp大的数
            left += 1
        li[right] = li[left]
    li[left] = tmp#将tmp归位
       
    return left
   
# 下面定义快速排序
def quick_sort(li,left,right):
    if left<right:
        mid = partition(li,left,right)#此时说明中间位置的已经分好啦，下面使用递归
        quick_sort(li,mid+1,right)
        quick_sort(li,left,mid-1)
li = [5,2,1,6,4,3,7]
quick_sort(li,0,len(li)-1)
print(li)

[1, 2, 3, 4, 5, 6, 7]

1.3算法分析

快速排序就和它的名字一样，比我们之前介绍的排序算法都要快，它的时间复杂度具体如下：

• 最差情况：$O(n^2)$
• 最好情况：$O(nlogn)$
• 平均情况：$O(nlogn)$
• 稳定性：不稳定
• 空间：需要$O(logn)到O(n)$

2.计数排序

2.1 基本思想

• 数据是比较集中的，最大值和最小值相差比较小
• 当重复值较多时

基本思想是，根据最大值和最小值，构建一个抽屉，然后按顺序往里面放元素并记住次数，最后再按顺序将数字拿出来。假设列表为[4,4,3,2,2,7,7],计数排序具体如下图所示：

2.2代码实现

def count_sort(li):    
    """首先要找出最大值和最小值"""
    mmax, mmin = li[0], li[0]#初始化最小值和最大值
    for i in range(1, len(li)):
        if (li[i] > mmax): 
            mmax = li[i]
        elif (li[i] < mmin): 
            mmin = li[i]
    nums = mmax - mmin+1#抽屉的个数
    counts = [0] * nums#首先用0来代替
    """将数据放进抽屉里面并记数"""
    for i in range (len(li)):
        counts[li[i] - mmin] = counts[li[i] - mmin] +1
    """将数据拿出来"""
    pos = 0
    for i in range(nums):
        for j in range(counts[i]):
            li[pos] = i + mmin
            pos += 1             
li = [4,4,3,2,2,7,7]

[2, 2, 3, 4, 4, 7, 7]

2.3 算法分析

计数排序的时间复杂度是$O(n)$，可以看出比我们之前介绍的排序算法都要快，但是，它有一个问题就是需要内存去存储那个抽屉，因此，往往在范围比较小，重复值较多的情况下使用。

• 最坏情况下:$O(n)$
• 最好情况下:$O(n)$
• 平均情况：$O(n)$
• 稳定性：稳定
• 需要额外的存储空间

3.归并排序

3.1 基本思想

归并排序是采用分治法的一个非常典型的应用。
分而治之

分：

• 递归拆分数组，直到分成单个数组为止
• 将将这些单个元素中的每一个与它的对合并,然后将这些对与它们的对等合并， 直到整个列表按照排序顺序合并为止.

治：

• 将2个排序列表合并为另一个排序列表是很简单的
• 简单地通过比较每个列表的头,删除最小的,以加入新排序的列表.

归并排序的思想就是先递归分解数组，再合并数组。将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

如下图所示所示：

左图是将数组分开，右图是将数组合并起来。下面我们来进一步看一下具体的实现过程：

3.2代码实现

def _merge(a, b):
    """合并两个列表"""
    c = []
    while len(a) > 0 and len(b) > 0:
        if a[0] < b[0]:
            c.append(a[0])#首先添加小的
            a.remove(a[0])#然后删除，移位比较
        else:
            c.append(b[0])
            b.remove(b[0])
    if len(a) == 0:
        c += b
    else:
        c += a
    return c
def _merge_sorted(nums):
    """通过递归实现排序"""
    if len(nums) <= 1:
        return nums
    m = len(nums) // 2#拆分数组
    a = _merge_sorted(nums[:m])#运用递归对后半部分排序，此时a是排好序的
    b = _merge_sorted(nums[m:])#运用递归对前半部分排序，此时b是排好序的
    return merge(a, b)#合并两个列表
def merge_sorted(nums, reverse=False):
    """归并排序"""
    nums = _merge_sorted(nums)
    if reverse:#降序还是升序，默认是升序
        nums = nums[::-1]
    return nums

l = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
l = merge_sorted(l)
print(l)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

3.3 算法分析

归并排序的时间复杂度情况如下

• 最坏情况下:$O(nlogn)$
• 最好情况下:$O(nlogn)$
• 平均情况：$O(nlogn)$
• 稳定性：稳定
• 需要额外的存储空间：$O(n)$

本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！