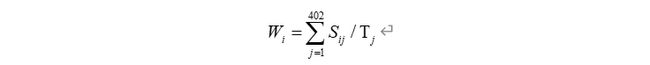2021年数学建模国赛C题问题二详细思路和代码
2021年数学建模国赛C题问题一详细思路和代码
说明:
本思路仅为小编个人思路,其中关于本文中给出的AdaBoost回归预测模型于今年的 国赛参考评分标准有所出入,所以本题思路为个人创新思路,不一定符合评分标准
1 问题分析
问题二要求我们首先参考问题一,在满足企业生产需求的情况下,找出最少需要多少家供应商提供原材料。分析后,我们发现企业每周有固定的产能,并且也有固定的订货量,且要求我们尽可能保持不少于满足两周的生产需求的原材料库存量。所以为了满足上述需求,我们考虑按照供应商的重要性大小不断加入新的供应商,以达到本周原料充足,且适当保证库存满足两周生产需求的目的。
关于企业未来的订货量,因为涉及到企业的订购方案,我们应该首先确定未来24周原材料的需求情况,由此确定企业对于原材料ABC的订货量。从之前的数据分析来看,企业的订货量呈周期性变化,于是我们统计企业5年内每一周原材料ABC的订货量,并作为学习样本,借助AdaBoost集成学习回归模型进行训练,预测出未来24周企业在原材料ABC上的订货量。然后,为了将每一周的原材料分到每个供应商上,形成每个供应商的预计订货量,我们应该对供应商的供货能力进行了量化。进而依据供应商的供货能力,得到每个企业对供应商的预计订货量。
关于订货方案的优化,我们应该考虑以经济效益为优化目标,以原有预计订货量作为初始值,生成企业的订货方案,其可能性很多,是典型的NP难问题,故想到借助模拟退火算法对经济效益与订货方案进行优化。不难发现,如何量化24周企业的经济效益是问题的关键,本题存在时间序列问题,且题目要求我们要制定未来24周每周最经济的订购方案,所以应该合理考虑到这些问题,制定衡量企业未来24周经济效益的模型。
关于转运方案,此问题是在已经优化好的原料订购方案下进行研究,故考虑生成不同的转运方案,最后通过模拟退火算法对转运过程的损耗进行优化,要求损耗最小。
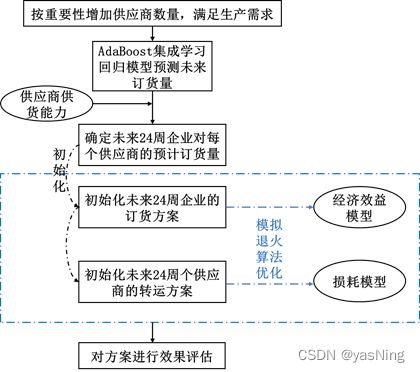
最后结合经济效益的优化情况、企业产能情况和损耗情况对订购方案和转运方案的效果进行分析。问题二的思路图如下:
2 满足生产需求的最少供应商数量的确定
为了找到满足生产需求的最少的供应商个数,我们本着“必须满足每周的产能(生产所需的原材料)”,“尽量满足两周的产能”的宗旨,对本问题进行求解。
首先我们可以计算一周中当前所有供应商提供的原料总和,进而通过原材料产能转换关系,计算得到原料可实现的产能。下面给出供货商数量不同的情况下,第 周产能 的计算方法。
3 AdaBoost集成学习回归模型预测未来24周企业的订货量
通过问题一中的数据分析,我们发现企业的订货量呈现周期性,且轮回周期大概为24周,所以我们考虑利用最后24周的订货数据,对未来24周的企业各原材料的订货量进行预测。
首先,我们统计了最后24周中每周企业对于原材料ABC的订购数量,以此作为数据,进行回归预测。在综合试验了多种回归方法后,我们最终选择了精度较高的AdaBoost集成学习回归模型,它是一种可将弱学习器提升为强学习器的算法,能对特定的数据分布进行学习,所以非常适合本题中的周期性数据回归。
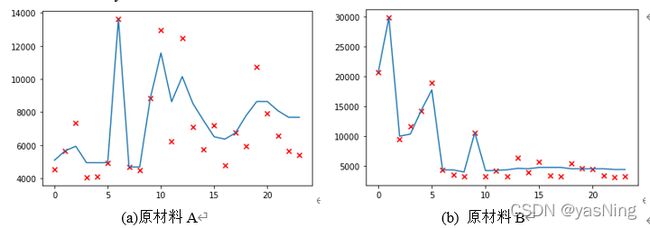
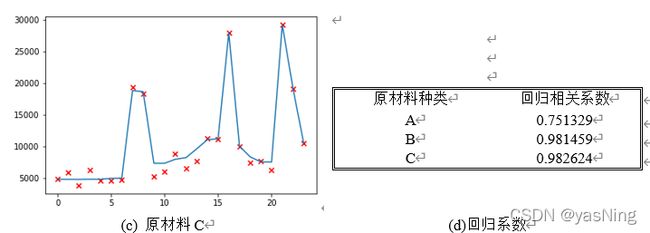
下面利用Python得到的AdaBoost算法的拟合回归图,以及其拟合相关系数:
利用回归模型,我们可以轻松的对未来24周企业在原材料ABC的订货量进行预测,利用预测的数据,基于供应商的供货能力,进行原材料预分配,得到上文所说的企业在供应商中的原材料预计订货量。下面给出它的计算方法:

4 经济效益模型与订货方案
从本题来看,企业的经济效益与原料的采购成本、订购方案和时间序列均有较大关系,题目中要求的是对未来24周的经济效益进行衡量。考虑到时序对经济效益的影响性,我们只考虑5年数据中的最后24周,对并其进行深入分析:
4.1 经济效益中时间序列的权重确定
问题一中已经对供应商的重要性进行了区分,选出了50家最重要的企业,这里我们认为重要的供应商其能给企业带来更好的经济效益。于是我们想到为后24周中的402家供应商赋予标签,其中最重要的50家给定标签为1,即:经济效益好,其余的供应商给定标签为0。那么此时的数据就变成了经济效益好与不好的供应商在24周内的供货量,以及他们的原材料价格。我们认为这些数据体现了供应商给企业带来的经济效益,那么这些数据与供应商的经济效益的关系变成了我们探究的问题。
为了探究时序和供货量对供应商经济效益的影响,我们先移除了价格这一栏,得到了经济效益好与不好的样本数据集。因为我们最后的确定240周对经济效益的重要程度,所以我们想到了随机森林算法,它可以在训练结束后,返回每个属性节点的权重数值,即每一个属性节点的重要性[4]。这刚好契合我们本题要解决的问题,所以我们最后借助随机森林算法,合理划分训练集测试集进行训练,在精度较高的情况下,给出24周每一周的重要性程度,并结合供货量和价格,对经济效益进行量化。
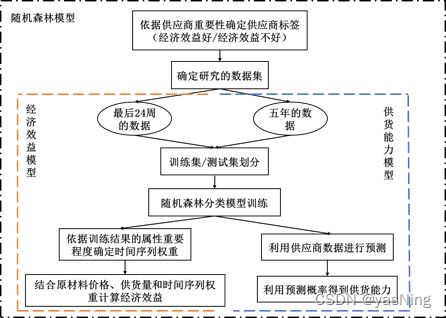
另外,供货能力也可以借助刚刚建立的经济效益模型得以量化,因为我们在训练后做预测时,是利用某一个供应商的供货数据得到经济效益好的概率,概率越大则它对企业的经济效益越好。前文提到的供货能力其实也是供应商重要性和经济效益的体现,所以我们认为预测出来经济效益好的供应商,它的供货能力也较高,把预测出来的概率当作供货能力,这样就得到了供应商的供货能力。但是值得注意的是,在探究时序权重问题时,我们是用最后24周的数据来进行训练的。而对于供货能力来讲,我们应当考虑5年中的整体数据,这更能反映供应商的实际水平,故这一部分采用5年的数据,借助随机森林算法进行量化。
本部分的具体思路如上图。
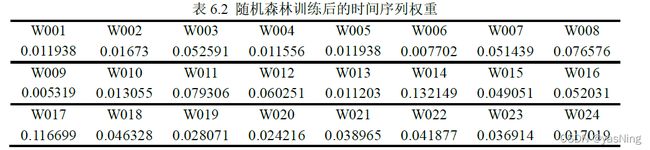
基于此模型,我们利用Python进行了训练,模型测试精度达到了92.59%左右,同时得到了时间序列权重如下表:
4.2 经济效益的计算、供货能力的量化与订货方案的产生方式
下面先给出经济效益的计算方法,它需要利用随机森林算法训练后得到的权重、供货量和原材料价格计算得到。本题研究的虽然是24周每周最经济的原材料订购方案,但是我们通过确定时间序列权重能很好的解释每周最经济这一问题。在我们训练时,是以提高预测经济效益的准确性为目的,这样训练出来的结果,本身就能反映每一周对于预测经济效益的贡献,所以自然达到了每周最经济的效果。下面给出24周经济效益的计算公式:


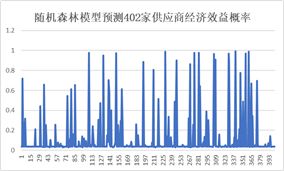
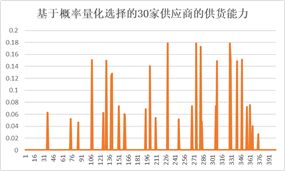
下图是随机森林预测的402家供应商经济效益概率图和基于此概率量化已选择的30家供应商的供货能力的结果:
5 运输损耗模型与转运方案
要在经济效益最好的订购方案的基础上优化转运损耗,必须明确原料运输过程的损耗计算方法,以及转运方案的产生方式。所以,在引入模拟退火算法优化之前,我们先对以上两个问题进行讨论。
运输损耗模型较为简单,在已有转运方案的前提下,结合转运商的运输损耗率即可给出计算公式:
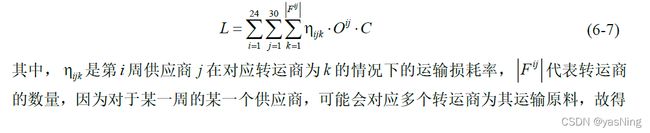

5.1 转运方案
我们研究的依然是未来24周的转运方案,且分析发现转运商的运输损耗变化依然呈周期性变化,变化周期大概为24周一轮。所以首先还是基于5年中后24周转运商的运输损耗数据,利用AdaBoost集成学习算法对未来24周转运商的运输损耗率进行回归预测,得到相应的运输损耗率。相关回归结果如下表:

从结果来看只有T4的回归系数较低,说明这组数据拟合的并不是很好,我们对原始数据进行了可视化,如图所示:
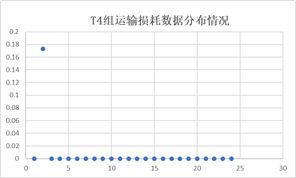
图中信息显示T4组数据存在大量零值,所以拟合效果较差属于正常现象,故我们接受预测结果出现大量0的情况。
利用AdaBoost算法预测得到未来24周的运输损耗率之后,我们就可以利用这个数据对转运方案的产生进行具体讨论了。
为了能在后面能利用模拟退火算法对转运方案进行优化,我们必须保证转运方案解的随机性,下面给出在保证每个供应商都能分配到合适的转运商的情况下,转运方案的初始化条件:

6 基于模拟退火算法的经济效益和运输损耗优化模型
6.1 目标函数模型
前文已经对量化经济效益的模型和量化运输损耗的模型进行了详细讨论,同时给出了订购方案和转运方案的生成方式,现在只需对模型嵌入优化算法即可。在引入优化算法之前,我们给出两个问题的目标函数:
6.2 模拟退火算法
上述两个优化问题均为典型的NP难问题,无法用确定性的方法求出全局的最优解,无法用非线性规划问题中算法函数进行求解,所以我们考虑用用模拟退火算法进行迭代,根据模拟退火算法的智能性快速找到问题的“最优解”。
6.3 优化结果分析
在实际优化过程中,我们选取外循环500次,内循环100次,初始温度 给定为1000,温度衰减系数 为0.98。
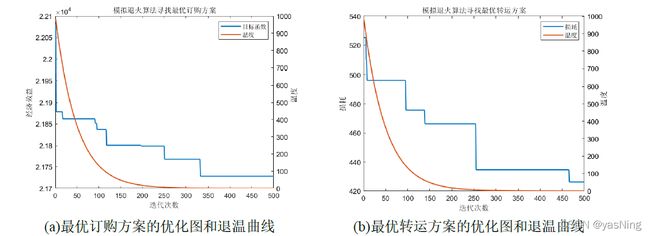
如优化结果所示,我们首先对企业经济效益进行了优化,给出了满足未来24周每周经济效益最高的订购方案,此时企业的经济花销大概为21728单位左右。然后我们在最优订购方案下,又对运输损耗进行了优化,给出了满足未来24周损耗最小的转运方案,此时企业的损耗大概为426单位左右。注意这里两个最优值的数据单位意义不一样,且订购方案中计算得到的花销是经过权重处理得,不能拿来比较。
而且我们的优化曲线符合模拟退火算法的基本理论,在寻找最优解的过程中,前期搜索范围较大,所得到的函数值不是很好,但是随着迭代次数的增加最优值逐渐稳定。
优化后的部分订货方案和转运方案如下
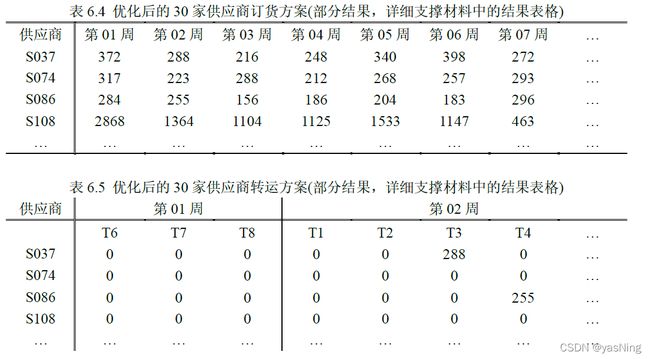
6.7 实施效果分析
企业实际运转时,库存产能非常重要,它一定程度上衡量了企业在未来抗击突发情况的能力。为了分析我们方案的实施效果,我们把优化前后的方案满足未来几周的产能情况作为分析的依据。统计未来24周中能满足未来产能需求的数量,并计算其比例,得到了下图所示的结果:
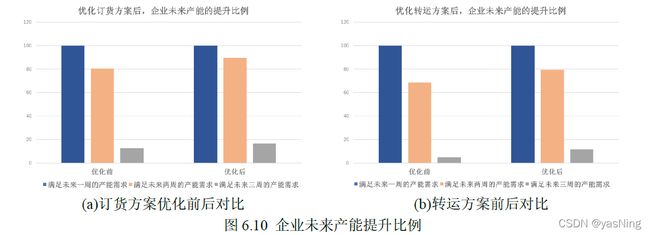
从图上来看,虽然我们的优化目标不是产能,但是通过优化订货方案和转运方案后,从实际实施效果来看,企业每一周在满足未来两周和三周的产能需求上,均得到了或多或少的提升。转运方案的整体数值比例明显低于订货方案,这与转运时损耗丢失的原料是相关的,原料损失了,自然也就很难满足未来几周的产能需求。订货方案本身不考虑运输损失,所以理论的产能应该大于把转运考虑在内的情况。但是通过对损失进行优化,一定程度上可以较少原料的损失,提高产能,所以图中显示的结果是有理论依据的。
以上就是小编对2021数学建模国赛C题 问题二 的详细解答思路了,因为上述思路具有争议性,所以仅供思维开拓哦。
下面也附上问题二的部分代,供大家参考:
1 MATLAB代码
计算采购成本
%% 计算采购成本
function [money, money_all] = compute_money(plan, class)
money = zeros(24, 1);
load('weight.mat');
money_all = 0;
%计算每周ABC三种原材料的量
for i = 1:24
A = 0;
B = 0;
C = 0;
for j = 1:402
if class(j) == 1.2
A = A + plan(j, i);
elseif class(j) == 1.1
B = B + plan(j, i);
elseif class(j) == 1
C = C + plan(j, i);
end
end
money(i) = A * 1.2 + B * 1.1 + C * 1;
money_all = money_all + money(i) * weight(i);
end
end
计算损耗=损耗量*材料单价
%% 计算损耗=损耗量*材料单价
function [W] = compute_waste(plan, waste, class)
W = 0;
for i = 1:24
for j = 1:402
wasteage = 0;
for t = 1:8
wastage = wasteage + plan(j, (i - 1) * 8 + t) * waste(t, i) / 100;
end
W = W + wastage * class(j);
end
end
end
对订购方案的实施效果分析
%% 对订购方案的实施效果分析
order_plan = xlsread('..\附件A 订购方案数据结果.xlsx', '问题2的订购方案结果', 'B7:Y408');
%未初始化时
% load('order_plan.mat');
%库存产能
capacity = 0;
satisfy_0 = 0;
satisfy_1 = 0;
satisfy_2 = 0;
satisfy_3 = 0;
load('..\prob.mat');
% 供货商的材料种类
class = prob(:, 3);
for i = 1:24
for j = 1:402
if class(j) == 1.2
capacity = order_plan(j, i) / 0.6 + capacity;
elseif class(j) == 1.1
capacity = order_plan(j, i) / 0.66 + capacity;
elseif class(j) == 1
capacity = order_plan(j, i) / 0.72 + capacity;
end
end
if capacity >= 2.82 * 1e4 * 3
satisfy_3 = satisfy_3 + 1;
elseif capacity >= 2.82 * 1e4 * 2
satisfy_2 = satisfy_2 + 1;
elseif capacity >= 2.82 * 1e4
satisfy_1 = satisfy_1 + 1;
else
satisfy_0 = satisfy_0 + 1;
end
capacity = capacity - 2.82 * 1e4;
end
disp('订购方案实施效果分析结果:');
disp('满足三周生产需求的百分比:');
disp(satisfy_3 / 24 * 100);
disp('满足两周生产需求的百分比:');
disp((satisfy_3 + satisfy_2) / 24 * 100);
disp('满足一周生产需求的百分比:');
disp((satisfy_1 + satisfy_3 + satisfy_2) / 24 * 100);
disp('不能满足一周生产需求的百分比:');
disp(satisfy_0 / 24 * 100);
%% 对转运方案的实施效果分析
trans_plan = xlsread('..\附件B 转运方案数据结果.xlsx', '问题2的转运方案结果', 'B7:GK408');
%未优化时
% load('trans_plan.mat');
load('..\predict_waste.mat');
capacity = 0;
satisfy_0 = 0;
satisfy_1 = 0;
satisfy_2 = 0;
satisfy_3 = 0;
for i = 1:24
for j = 1:402
wasteage = 0;
for t = 1:8
wasteage = wasteage + trans_plan(j, (i - 1) * 8 + t) * predict_waste(t, i) / 100;
end
if class(j) == 1.2
capacity = (order_plan(j, i) - wasteage) / 0.6 + capacity;
elseif class(j) == 1.1
capacity = (order_plan(j, i) - wasteage) / 0.66 + capacity;
elseif class(j) == 1
capacity = (order_plan(j, i) - wasteage) / 0.72 + capacity;
end
end
if capacity >= 2.82 * 1e4 * 3
satisfy_3 = satisfy_3 + 1;
elseif capacity >= 2.82 * 1e4 * 2
satisfy_2 = satisfy_2 + 1;
elseif capacity >= 2.82 * 1e4
satisfy_1 = satisfy_1 + 1;
else
satisfy_0 = satisfy_0 + 1;
end
capacity = capacity - 2.82 * 1e4;
end
disp('转运方案实施效果分析结果:');
disp('满足三周生产需求的百分比:');
disp(satisfy_3 / 24 * 100);
disp('满足两周生产需求的百分比:');
disp((satisfy_3 + satisfy_2) / 24 * 100);
disp('满足一周生产需求的百分比:');
disp((satisfy_1 + satisfy_3 + satisfy_2) / 24 * 100);
disp('不能满足一周生产需求的百分比:');
disp(satisfy_0 / 24 * 100);
2 PYTHON 代码
AdaBoost预测ABC原料产量
from scipy import io
import numpy as np
import matplotlib.pyplot as plt
#读取数据
data = io.loadmat('ABC.mat')
feature = data['class_week']
Y = feature.T
x1 = []
x2 = []
x3 = []
for i in range(24):
x1.append(i)
x2.append(i)
x3.append(i)
X1 = np.array(x1)
X1 = X1.reshape(24,1)
X2 = np.array(x2)
X2 = X2.reshape(24,1)
X3 = np.array(x3)
X3 = X3.reshape(24,1)
y1 = Y[0]
y1 = y1[215:239]
y2 = Y[1]
y2 = y2[215:239]
y3 = Y[2]
y3 = y3[215:239]
plt.scatter(X1,y1, label="train", c="red", marker="x")
from sklearn.ensemble import AdaBoostRegressor
clf1 = AdaBoostRegressor(random_state=0, n_estimators=100).fit(X1,y1)
clf2 = AdaBoostRegressor(random_state=0, n_estimators=100).fit(X2,y2)
clf3 = AdaBoostRegressor(random_state=0, n_estimators=100).fit(X3,y3)
print(clf1.score(X1,y1))
print(clf2.score(X2,y2))
print(clf3.score(X3,y3))
Y_predict = clf1.predict(X1)
##要预测的 横坐标 x 输入 predict函数 用 y_predict接收
y_predict = clf1.predict([[1]])
plt.plot(X1,Y_predict)
plt.show()
plt.scatter(X2,y2, label="train", c="red", marker="x")
Y_predict2 = clf2.predict(X2)
##要预测的 横坐标 x 输入 predict函数 用 y_predict接收
y_predict2 = clf2.predict([[1]])
plt.plot(X2,Y_predict2)
plt.show()
plt.scatter(X3,y3, label="train", c="red", marker="x")
Y_predict3 = clf3.predict(X3)
##要预测的 横坐标 x 输入 predict函数 用 y_predict接收
y_predict3 = clf3.predict([[1]])
plt.plot(X3,Y_predict3)
plt.show()
x1_pre = []
x2_pre = []
x3_pre = []
for j in range(24):
x1_pre.append(j)
x2_pre.append(j)
x3_pre.append(j)
X1_pre = np.array(x1_pre)
X1_pre = X1_pre.reshape(24,1)
X2_pre = np.array(x2_pre)
X2_pre = X2_pre.reshape(24,1)
X3_pre = np.array(x3_pre)
X3_pre = X3_pre.reshape(24,1)
predict_y1 = clf1.predict(X1_pre)
predict_y2 = clf2.predict(X2_pre)
predict_y3 = clf3.predict(X3_pre)
io.savemat("./predict_A.mat", {'predict_A':predict_y1})
io.savemat("./predict_B.mat", {'predict_B':predict_y2})
io.savemat("./predict_C.mat", {'predict_C':predict_y3})
随机森林模型
# -*- coding: utf-8 -*-
#随机森林实现
from sklearn.ensemble import RandomForestClassifier
from scipy import io
import numpy as np
#数据集初始化
feature = io.loadmat('supply_oneweek.mat')
feature = feature['unnamed']
label = io.loadmat('label.mat')
label = label['label']
Label = label[:,1]
clf = RandomForestClassifier(criterion = 'gini',max_depth=4,random_state=0)
clf.fit(feature,Label)
print("随机森林精度:",clf.score(feature,Label))
weight = clf.feature_importances_
prob = clf.predict_proba(feature)
io.savemat("./weight.mat", {'weight':weight})
io.savemat("./prob.mat", {'prob':prob})