算法：哈希表

哈希表简介

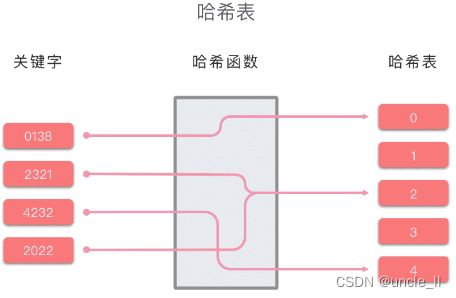
哈希表：也叫做散列表。是根据关键字和值（Key-Value）直接进行访问的数据结构。也就是说，它通过关键字 key 和一个映射函数 Hash(key) 计算出对应的值 value，然后把键值对映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做哈希函数（散列函数），用于存放记录的数组叫做 哈希表（散列表）。
哈希表的关键思想是使用哈希函数，将键 key 和值 value 映射到对应表的某个区块中。可以将算法思想分为两个部分：

• 向哈希表中插入一个关键字：哈希函数决定该关键字的对应值应该存放到表中的哪个区块，并将对应值存放到该区块中
• 在哈希表中搜索一个关键字：使用相同的哈希函数从哈希表中查找对应的区块，并在特定的区块搜索该关键字对应的值

哈希表的原理示例图如下所示：

• 插入关键字：哈希函数对关键字进行哈希，得到哈希值后插入到哈希表对应的地方
• 搜索关键字：哈希函数对关键字进行哈希，基于哈希值去哈希表中进行查询

哈希表的应用举例：

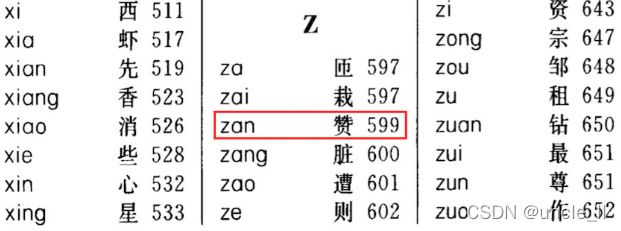
哈希表在生活中的应用也很广泛，其中一个常见例子就是「查字典」。
比如为了查找赞这个字的具体意思，我们在字典中根据这个字的拼音索引 zan，查找到对应的页码为 599。然后我们就可以翻到字典的第 599 页查看赞字相关的解释了。

查找索引这一过程可以看作是哈希函数操作

---

哈希函数

哈希函数：将哈希表中元素的关键键值映射为元素存储位置的函数。
哈希函数是哈希表中最重要的部分。一般来说，哈希函数会满足以下几个条件：

• 哈希函数应该易于计算，并且尽量使计算出来的索引值均匀分布，这能减少哈希冲突
• 哈希函数计算得到的哈希值是一个固定长度的输出值
• 如果 Hash(key1) 不等于 Hash(key2)，那么 key1、key2 一定不相等
• 如果 Hash(key1) 等于 Hash(key2)，那么 key1、key2 可能相等，也可能不相等（会发生哈希碰撞）

在哈希表的实际应用中，关键字的类型除了数字类型，还有可能是字符串类型、浮点数类型、大整数类型，甚至还有可能是几种类型的组合。一般会将各种类型的关键字先转换为整数类型，再通过哈希函数，将其映射到哈希表中。
而关于整数类型的关键字，通常用到的哈希函数方法有：直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。

下面介绍几个常用的哈希函数方法。

直接定址法

直接定址法：取关键字或者关键字的某个线性函数值为哈希地址。即：$Hash(key)=key$ 或者 $Hash(key)=a\ast key+b$，其中 a 和 b 为常数。

这种方法计算最简单，且不会产生冲突。适合于关键字分布基本连续的情况，如果关键字分布不连续，空位较多，则会造成存储空间的浪费。

举一个例子，假设有一个记录了从 1 岁到 100 岁的人口数字统计表。其中年龄为关键字，哈希函数取关键字自身，如下表所示。

比如想要查询 25 岁的人有多少，则只要查询表中第 25 项即可。

除留余数法

除留余数法：假设哈希表的表长为 m，取一个不大于 m 但接近或等于 m 的质数 p，利用取模运算，将关键字转换为哈希地址。即：$Hash(key)=key$，其中 p 为不大于 m 的质数。

这也是一种简单且常用的哈希函数方法。其关键点在于p 的选择。根据经验而言，一般 p 取素数或者 m，这样可以尽可能的减少冲突。

比如我们需要将 7 个数 [432, 5, 128, 193, 92, 111, 88] 存储在 11 个区块中（长度为 11 的数组），通过除留余数法将这 7 个数应分别位于如下地址：

比如432，对11取余数，余数为3，放在03位置

平方取中法

平方取中法：先通过求关键字平方值的方式扩大相近数之间的差别，然后根据表长度取关键字平方值的中间几位数为哈希地址。

比如：$Hash(key)=(key\ast key)//100\%1000$，先计算平方，去除末尾的2位数，再取中间 3 位数作为哈希地址。
这种方法因为关键字平方值的中间几位数和原关键字的每一位数都相关，所以产生的哈希地址也比较均匀，有利于减少冲突的发生。

比如关键字为1443， 进行哈希计算：

$1443\ast 1443=2082249$

$2082249/100=20822$

$20822\%1000=822$

因此最终的哈希值结果就是822

基数转换法

基数转换法：将关键字看成另一种进制的数再转换成原来进制的数，然后选其中几位作为哈希地址。

比如，将关键字看作是13进制的数，再将其转变为10进制的数，然后将其作为哈希地址。

以343246为例，计算方式如下：

$$(343246{)}_{13}=3\ast 13^5+4\ast 13^4+3\ast 13^3+2\ast 13^2+4\ast 13^1+6\ast 13^0=(1235110{)}_{10}$$

---

哈希冲突

哈希冲突：不同的关键字通过同一个哈希函数可能得到同一哈希地址，即 key1 ≠ key2，而 Hash(key1) = Hash(key2)，这种现象称为哈希冲突。

理想状态下，我们的哈希函数是完美的一对一映射，即一个关键字（key）对应一个值（value），不需要处理冲突。但是一般情况下，不同的关键字 key 可能对应了同一个值 value，这就发生了哈希冲突。

设计再好的哈希函数也无法完全避免哈希冲突。所以就需要通过一定的方法来解决哈希冲突问题。常用的哈希冲突解决方法主要是两类：「开放地址法」和「链地址法」。

开放地址法

开放地址法：指的是将哈希表中的「空地址」向处理冲突开放。当哈希表未满时，处理冲突时需要尝试另外的单元，直到找到空的单元为止。

当发生冲突时，开放地址法按照下面的方法求得后继哈希地址：$H(i)=(Hash(key)+F(i))\%m，i=1,2,3,...,n(n\le m-1)$。

• H(i) 是在处理冲突中得到的地址序列。即在第 1 次冲突（i = 1）时经过处理得到一个新地址 H(1)，如果在 H(1) 处仍然发生冲突（i = 2）时经过处理时得到另一个新地址 H(2) …… 如此下去，直到求得的 H(n) 不再发生冲突
• Hash(key) 是哈希函数，m 是哈希表表长，取余目的是为了使得到的下一个地址一定落在哈希表中
• F(i) 是冲突解决方法，取法可以有以下几种：
  • 线性探测法：$F(i)=1,2,3,...,m-1$
  • 二次探测法：$F(i)=1^2,-1^2,2^2,-2^2,...,n^2(n\le m/2)$
  • 伪随机数序列：F(i) = 伪随机数序列

开放地址法举例

举例说明一下如何用以上三种冲突解决方法处理冲突，并得到新地址 H(i)。例如，在长度为 11 的哈希表中已经填有关键字分别为 28、49、18 的记录（哈希函数为 Hash(key) = key % 11）。

现在将插入关键字为 38 的新纪录，根据哈希函数得到的哈希地址为 5，产生冲突。接下来分别使用这三种冲突解决方法处理冲突。

• 使用线性探测法：得到下一个地址 $H(1)=(5+1)\%11=6$，仍然冲突；继续求
  出 $H(2)=(5+2)\%11=7$，仍然冲突；继续求出 $H(3)=(5+3)\%11=8$，8
  对应的地址为空，处理冲突过程结束，记录填入哈希表中序号为 8 的位置。

• 使用二次探测法：得到下一个地址 $H(1)=(5+1\ast 1)$，仍然冲突；继续
  求出 $H(2)=(5-1\ast 1)$，4 对应的地址为空，处理冲突过程结束，记录
  填入哈希表中序号为 4 的位置。

• 使用伪随机数序列：假设伪随机数为 9，则得到下一个地址$ H(1) = (9 + 5) % 11
  = 3$，3 对应的地址为空，处理冲突过程结束，记录填入哈希表中序号为 3 的位置。

3.2 链地址法

链地址法：将具有相同哈希地址的元素（或记录）存储在同一个线性链表中。
链地址法是一种更加常用的哈希冲突解决方法。相比于开放地址法，链地址法更加简单。
假设哈希函数产生的哈希地址区间为[0, m - 1]，哈希表的表长为 m。则可以将哈希表定义为一个有 m 个头节点组成的链表指针数组 T。

• 这样在插入关键字的时候，只需要通过哈希函数 Hash(key) 计算出对应的哈希地址 i，然后将其以链表节点的形式插入到以 T[i] 为头节点的单链表中。在链表中插入位置可以在表头或表尾，也可以在中间。如果每次插入位置为表头，则插入操作的时间复杂度为 O(1)。
• 而在在查询关键字的时候，只需要通过哈希函数 Hash(key) 计算出对应的哈希地址 i，然后将对应位置上的链表整个扫描一遍，比较链表中每个链节点的键值与查询的键值是否一致。查询操作的时间复杂度跟链表的长度 k 成正比，也就是 $O(k)$。对于哈希地址比较均匀的哈希函数来说，理论上讲，$k=n//m$，其中 n 为关键字的个数，m 为哈希表的表长。

相对于开放地址法，采用链地址法处理冲突要多占用一些存储空间（主要是链节点占用空间）。但它可以减少在进行插入和查找具有相同哈希地址的关键字的操作过程中的平均查找长度。这是因为在链地址法中，待比较的关键字都是具有相同哈希地址的元素，而在开放地址法中，待比较的关键字不仅包含具有相同哈希地址的元素，而且还包含哈希地址不相同的元素。

链地址法举例

举例来说明如何使用链地址法处理冲突。

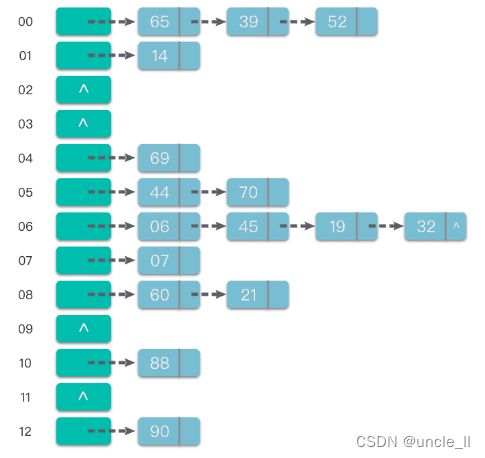
假设现在要存入的关键字集合 keys = [88, 60, 65, 69, 90, 39, 07, 06, 14, 44, 52, 70, 21, 45, 19, 32]。再假定哈希函数为 $Hash(key)=key\%13$，哈希表的表长 m = 13，哈希地址范围为[0, m - 1]。

将这些关键字使用链地址法处理冲突，并按顺序加入哈希表中（图示为插入链表表尾位置），最终得到的哈希表如下图所示。

$$keys=[88,60,65,69,90,39,07,06,14,44,52,70,21,45,19,32]$$

哈希表总结

本节讲解了一些比较基础、偏理论的哈希表知识。包含哈希表的定义，哈希函数、哈希冲突以及哈希冲突的解决方法。

• 哈希表：通过键 key 和一个映射函数 Hash(key) 计算出对应的值 value，把关键码值映射到表中一个位置来访问记录，以加快查找的速度
• 哈希函数：将哈希表中元素的关键键值映射为元素存储位置的函数
• 哈希冲突：不同的关键字通过同一个哈希函数可能得到同一哈希地址

哈希表的两个核心问题是：「哈希函数的构建」和「哈希冲突的解决方法」。

• 常用的哈希函数方法有：直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。
• 常用的哈希冲突的解决方法有两种：开放地址法 和 链地址法。

---

学习视频

• https://tianchi.aliyun.com/course/932/14648

哈希表相较于列表查找而言，速度要快很多，宽泛来说时间复杂度是$O(1)$，应用比较多，比如redis就是基于哈希表构建的数据库

---

例题

160 存在重复元素

给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。

示例 1：

输入：nums = [1,2,3,1]
输出：true

示例 2：

输入：nums = [1,2,3,4]
输出：false

示例 3：

输入：nums = [1,1,1,3,3,4,3,2,4,2]
输出：true

提示：

• $1<=nums.length<=10^5$
• $-10^9<=nums[i]<=10^9$

解题思路：

• 先对数组进行排序。排序之后，判断相邻元素之间是否出现重复元素。
• 使用哈希表，具体步骤如下：
  • 遍历数组中元素
  • 如果哈希表中出现了该元素，则说明出现了重复元素，直接返回 True
  • 如果没有出现，则在哈希表中添加该元素
  • 如果遍历完也没发现重复元素，则说明没有出现重复元素，返回 False

第二种需要占用新的空间，但是时间会快一些。这里以第二种哈希表实现

代码实现：

• python实现

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        count = dict()
        for num in nums:
            if num not in count:
                count[num] = 1
            else:
                return True
        return False

• c++实现

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        unordered_map<int, int> d;
        for(int x: nums)
        {
            if(d.find(x) != d.end())
            {
                return true;
            }
            d.insert({x, 1});
        }
        return false;
    }
};

---

33 有效的数独

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

• 一个有效的数独（部分已被填充）不一定是可解的。
• 只需要根据以上规则，验证已经填入的数字是否有效即可。
• 空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

• board.length == 9
• board[i].length == 9
• board[i][j] 是一位数字（1-9）或者 '.'

解题思路：

有效的数独满足以下三个条件：

• 同一个数字在每一行只能出现一次；
• 同一个数字在每一列只能出现一次；
• 同一个数字在每一个小九宫格只能出现一次。

可以使用哈希表记录每一行、每一列和每一个小九宫格中，每个数字出现的次数。只需要遍历数独一次，在遍历的过程中更新哈希表中的计数，并判断是否满足有效的数独的条件即可。因此考虑使用3个长度为9的哈希表数组，来表示该数字是否在所在的行，所在的列，所在的方格中出现过。整个方法具体步骤如下：

• 遍历代表数独的二维数组board
• 如果board[i][j]为.字符，继续判断下一个数独位置
• 判断该位置所在行，所在列，所在方格的哈希表中是否出现了该数字
• 如果出现了该数字，返回False
• 如果遍历完整个数独都没有出现重复数字，返回True

代码实现：

• python实现

class Solution:
    def isValidSudoku(self, board: List[List[str]]) -> bool:
        row_map = [dict() for _ in range(9)]
        cols_map = [dict() for _ in range(9)]
        boxs_map = [dict() for _ in range(9)]
        
        for i in range(9):
            for j in range(9):
                if board[i][j] == '.':
                    continue
                
                num = int(board[i][j])
                box_index = (i//3) * 3 + j // 3
                row_num = row_map[i].get(num, 0)
                col_num = cols_map[j].get(num, 0)
                box_num = boxs_map[box_index].get(num, 0)
                
                if row_num > 0 or col_num > 0 or box_num > 0:
                    return False
                
                row_map[i][num] = 1
                cols_map[j][num] = 1
                boxs_map[box_index][num] = 1
        return True

• c++实现

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
    
        int rows[9][9];
        int columns[9][9];
        int subboxes[3][3][9];
        
        memset(rows,0,sizeof(rows));
        memset(columns,0,sizeof(columns));
        memset(subboxes,0,sizeof(subboxes));
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                if (c != '.') {
                    int index = c - '0' - 1;
                    rows[i][index]++;
                    columns[j][index]++;
                    subboxes[i / 3][j / 3][index]++;
                    if (rows[i][index] > 1 || columns[j][index] > 1 || subboxes[i / 3][j / 3][index] > 1) {
                        return false;
                    }
                }
            }
        }
        return true;
    }
};

---

161 存在重复元素 II

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], k = 3
输出：true

示例 2：

输入：nums = [1,0,1,1], k = 1
输出：true

示例 3：

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

提示：

• $1<=nums.length<=10^5$
• $-10^9<=nums[i]<=10^9$
• $0<=k<=10^5$

解题思路：

• 哈希表，可以使用一个哈希表记录元素，key为元素，value为下标。如果遍历的时候发现哈希表中已经存在该元素了，那么比较哈希表中的下标与遍历的下标的关系是否满足<=k，如果满足，则返回True；如果不满足，则更新哈希表中的该元素对应的value为最新的下标，这样才能使得i-j的值尽可能的小

代码实现：

• python实现

class Solution:
    def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
        d = dict()
        for i, val in enumerate(nums):
            if val not in d:
                d[val] = i
            else:
                index = d[val]
                if i - index <= k:
                    return True
                else:
                    d[val] = i
        return False

• c++实现

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        unordered_map<int, int> d;
        int length = nums.size();
        for(int i=0; i<length; i++)
        {
            int num = nums[i];
            auto it = d.find(num);
            if(it != d.end())
            {
                int index = d[num];
                if(i-index <= k)
                {
                    return true;
                }
                else
                {
                    it->second = i;
                }
            }
            else
            {
                d[num] = i;
            }
        }
        return false;
    }
};

---

355 宝石与石头

给你一个字符串 jewels 代表石头中宝石的类型，另有一个字符串 stones 代表你拥有的石头。 stones 中每个字符代表了一种你拥有的石头的类型，你想知道你拥有的石头中有多少是宝石。

字母区分大小写，因此 "a" 和 "A" 是不同类型的石头。

示例 1：

输入：jewels = "aA", stones = "aAAbbbb"
输出：3

示例 2：

输入：jewels = "z", stones = "ZZ"
输出：0

提示：

• 1 <= jewels.length, stones.length <= 50
• jewels 和 stones 仅由英文字母组成
• jewels 中的所有字符都是 唯一的

解题思路：

• 哈希表：首先遍历jewels，并使用哈希表进行存储；其次遍历stones，然后判断元素是否在哈希表中，如果在的话，宝石个数+1

代码实现：

• python实现

class Solution:
    def numJewelsInStones(self, jewels: str, stones: str) -> int:
        d = dict()
        count = 0
        for s in jewels:
            d[s] = ''
        
        for s in stones:
            if s in d:
                count += 1
        return count

• c++实现

class Solution {
public:
    int numJewelsInStones(string jewels, string stones) {
        int count = 0;
        
        unordered_map <char, int> d;
        for(auto s: jewels)
        {
            d[s] = 1;
        }
        
        for(auto s: stones)
        {
            auto it = d.find(s);
            if(it != d.end())
            {
                count++;
            }
        }
        return count;
    }
};

---

374 子域名访问计数

网站域名 "discuss.leetcode.com" 由多个子域名组成。顶级域名为 "com" ，二级域名为 "leetcode.com" ，最低一级为 "discuss.leetcode.com" 。当访问域名 "discuss.leetcode.com" 时，同时也会隐式访问其父域名 "leetcode.com"以及 "com" 。

计数配对域名 是遵循 "rep d1.d2.d3" 或 "rep d1.d2" 格式的一个域名表示，其中 rep 表示访问域名的次数，d1.d2.d3 为域名本身。

• 例如，"9001 discuss.leetcode.com" 就是一个 计数配对域名 ，表示 discuss.leetcode.com 被访问了 9001 次。

给你一个 计数配对域名 组成的数组 cpdomains ，解析得到输入中每个子域名对应的 计数配对域名 ，并以数组形式返回。可以按 任意顺序 返回答案。

示例 1：

输入：cpdomains = ["9001 discuss.leetcode.com"]
输出：["9001 leetcode.com","9001 discuss.leetcode.com","9001 com"]
解释：例子中仅包含一个网站域名："discuss.leetcode.com"。
按照前文描述，子域名 "leetcode.com" 和 "com" 都会被访问，所以它们都被访问了 9001 次。

示例 2：

输入：cpdomains = ["900 google.mail.com", "50 yahoo.com", "1 intel.mail.com", "5 wiki.org"]
输出：["901 mail.com","50 yahoo.com","900 google.mail.com","5 wiki.org","5 org","1 intel.mail.com","951 com"]
解释：按照前文描述，会访问 "google.mail.com" 900 次，"yahoo.com" 50 次，"intel.mail.com" 1 次，"wiki.org" 5 次。
而对于父域名，会访问 "mail.com" 900 + 1 = 901 次，"com" 900 + 50 + 1 = 951 次，和 "org" 5 次。

提示：

• 1 <= cpdomain.length <= 100
• 1 <= cpdomain[i].length <= 100
• cpdomain[i] 会遵循 "repi d1i.d2i.d3i" 或 "repi d1i.d2i" 格式
• repi 是范围 [1, 104] 内的一个整数
• d1i、d2i 和 d3i 由小写英文字母组成

解题思路：

• 哈希表：每次先把前面的数字取出，然后从后向前遍历，遇到.就将后面的字符串放进哈希表，数量加上之前的，然后拼接成字符串即可

代码实现：

• python实现

class Solution:
    def subdomainVisits(self, cpdomains: List[str]) -> List[str]:
        hashmap = {}
        res = []
        def deal(string):
            nums, half_last = string.split(' ')
            nums = int(nums)  # 类型转换
            # 处理half_last
            str_ = ''
            for i in range(len(half_last)-1, -1, -1):
                if half_last[i] == '.':
                    if str_ in hashmap:
                        hashmap[str_] += nums
                    else:
                        hashmap[str_] = nums
                str_ = half_last[i] + str_
            # 将最长域名加入其中
            if half_last in hashmap:
                hashmap[half_last] += nums
            else:
                hashmap[half_last] = nums
        for ch in cpdomains:
            deal(ch)
        for k, v in hashmap.items():
            res.append(' '.join([str(v), k]))
        return res

• c++实现

class Solution {
private:
    vector<string> Split(const string& s, char c)
    {
        vector<string> res;
        stringstream ss(s);
        string curr;
        while(std::getline(ss, curr, c))
        {
            // cout << "[" <<  curr << "]" << endl;
            res.push_back(curr);
        }
        return res;
    }

public:
    vector<string> subdomainVisits(vector<string>& cpdomains) {
        // 保存数量映射的哈希表
        unordered_map<string, int> str2cnt;

        // 遍历去拆分字符串
        for (const string& cp : cpdomains)
        {
            vector<string> cc = Split(cp, ' ');
            vector<string> s = Split(cc[1], '.');
            int cnt = stoi(cc[0]);
            // 从后往前去构建字符串数组
            string curr = "";
            for (int i = s.size()-1; i >= 0; --i)
            {
                curr = s[i] + (curr.empty() ? "" : ".") + curr;
                str2cnt[curr] += cnt;
            }
        }

        vector<string> res;
        for (auto iter = str2cnt.begin(); iter != str2cnt.end(); ++iter)
        {
            res.push_back(to_string(iter->second) + " " + iter->first);
        }

        return res;
    }
};