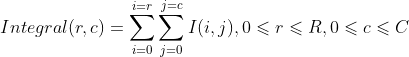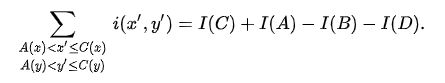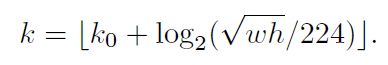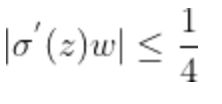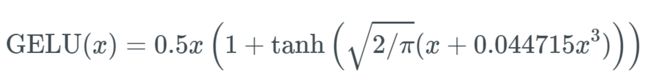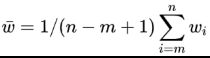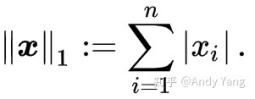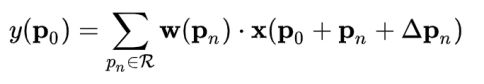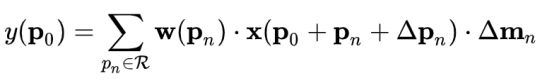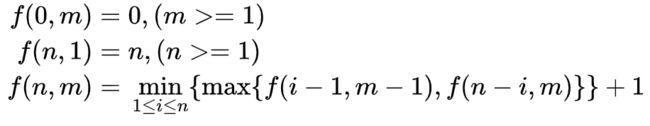面筋面筋.
编程题：
1，DAG（有向无环图），设计结构存储DAG，每个节点有一个类型名，判断DAG1中有多少子结构，使得其拓扑结构和对应结构的位置类型相同。讲思路，然后coding 讲code。
2，编程，用积分图的方式，实现均值滤波
积分图原理：
而且，积分图只需遍历一次图像即可有效地计算出来，因为积分图每一点(x,y)的值是：
所以，一旦积分图计算完毕，对任意矩形区域的和的计算就可以在常数时间内完成。如下图中，阴影矩形区域的和为：
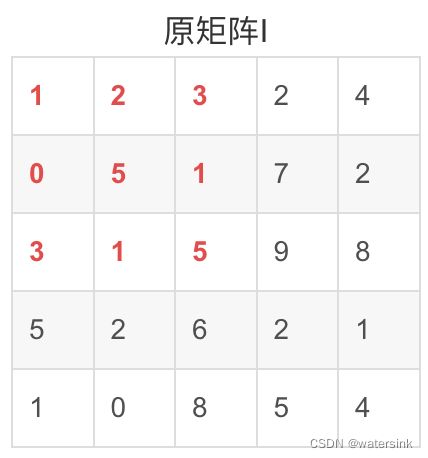
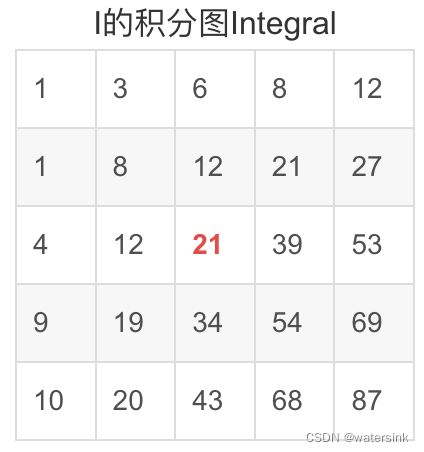
举个栗子，
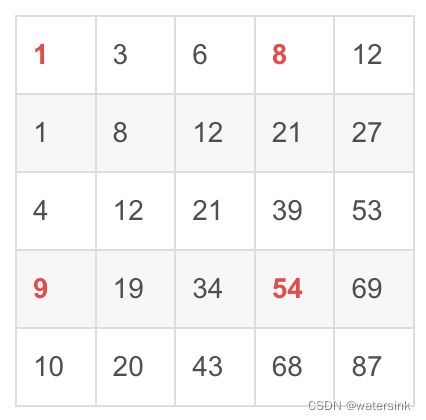
要求中间红色区域的和，只需对积分图进行如下计算：
也就是:5+1+7+1+5+9+2+6+2 = 54+1-8-9.
//积分图-常规方法
void Im_integral(cv::Mat& src,cv::Mat& dst){
int nr = src.rows;
int nc = src.cols;
dst = cv::Mat::zeros(nr + 1, nc + 1, CV_64F);
for (int i = 1; i < dst.rows; ++i){
for (int j = 1; j < dst.cols; ++j){
double top_left = dst.at(i - 1, j - 1);
double top_right = dst.at(i - 1, j);
double buttom_left = dst.at(i, j - 1);
int buttom_right = src.at(i-1, j-1);
dst.at(i, j) = buttom_right + buttom_left + top_right - top_left;
}
}
}
//积分图快速均值滤波
void Fast_MeanFilter(cv::Mat& src, cv::Mat& dst, cv::Size wsize){
//图像边界扩充
if (wsize.height % 2 == 0 || wsize.width % 2 == 0){
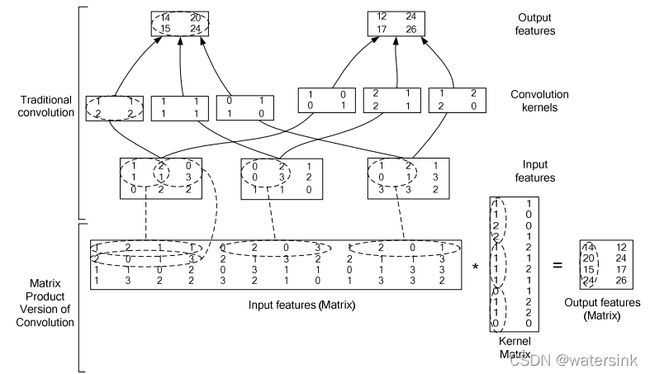
fprintf(stderr, "Please enter odd size!");
exit(-1);
}
int hh = (wsize.height - 1) / 2;
int hw = (wsize.width - 1) / 2;
cv::Mat Newsrc;
cv::copyMakeBorder(src, Newsrc, hh, hh, hw, hw, cv::BORDER_REFLECT_101);//以边缘为轴，对称
dst = cv::Mat::zeros(src.size(), src.type());
//计算积分图
cv::Mat inte;
Fast_integral(Newsrc, inte);
//均值滤波
double mean = 0;
for (int i = hh+1; i < src.rows + hh + 1;++i){ //积分图图像比原图（边界扩充后的）多一行和一列
for (int j = hw+1; j < src.cols + hw + 1; ++j){
double top_left = inte.at(i - hh - 1, j - hw-1);
double top_right = inte.at(i-hh-1,j+hw);
double buttom_left = inte.at(i + hh, j - hw- 1);
double buttom_right = inte.at(i+hh,j+hw);
mean = (buttom_right - top_right - buttom_left + top_left) / wsize.area();
//一定要进行判断和数据类型转换
if (mean < 0)
mean = 0;
else if (mean>255)
mean = 255;
dst.at(i - hh - 1, j - hw - 1) = static_cast (mean);
}
}
} 3，求两个字符串的最长公共子串
有两个字符串（可能包含空格）,请找出其中最长的公共连续子串,输出其长度。(长度在1000以内)
例如：
输入：abcde bcd
输出：3
解析
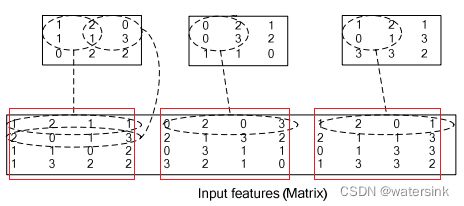
1、把两个字符串分别以行和列组成一个二维矩阵。
2、比较二维矩阵中每个点对应行列字符中否相等，相等的话值设置为1，否则设置为0。
3、通过查找出值为1的最长对角线就能找到最长公共子串。
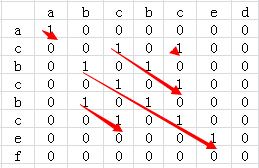
比如：str=acbcbcef，str2=abcbced，则str和str2的最长公共子串为bcbce，最长公共子串长度为5。
针对于上面的两个字符串我们可以得到的二维矩阵如下：
从上图可以看到，str1和str2共有5个公共子串，但最长的公共子串长度为5。
为了进一步优化算法的效率，我们可以再计算某个二维矩阵的值的时候顺便计算出来当前最长的公共子串的长度，即某个二维矩阵元素的值由record[i][j]=1演变为record[i][j]=1 +record[i-1][j-1]，这样就避免了后续查找对角线长度的操作了。修改后的二维矩阵如下：
递推公式为：
当A[i] != B[j]，dp[i][j] = 0
当A[i] == B[j]，若i = 0 || j == 0，dp[i][j] = 1，否则 dp[i][j] = dp[i - 1][j - 1] + 1
public int getLCS(String s, String t) {
if (s == null || t == null) {
return 0;
}
int result = 0;
int sLength = s.length();
int tLength = t.length();
int[][] dp = new int[sLength][tLength];
for (int i = 0; i < sLength; i++) {
for (int k = 0; k < tLength; k++) {
if (s.charAt(i) == t.charAt(k)) {
if (i == 0 || k == 0) {
dp[i][k] = 1;
} else {
dp[i][k] = dp[i - 1][k - 1] + 1;
}
result = Math.max(dp[i][k], result);
} else {
dp[i][k] = 0;
}
}
}
return result;
}4，全排列next_permutation：
基本思路：回溯+递归
任意选一个数（一般从小到大或者从左到右）打头，对后面的n-1个数进行全排列。通过递归，要得到n-1个数的全排列，需要先得到n-2个数的全排列，出口是只有一个数的全排列，因为只有一种就是他本身。
- 开始for循环
- 改变第1个元素为原始数组中的第1个元素
- 求第2个元素到第n个元素的全排列
- 要求第2个元素到第n个元素的全排列，要递归的求第3个元素到第n个元素的全排列......
- 直到递归到第n个元素到第n个元素的全排列，递归出口
- 将改变的数组返回
- 改变第一个元素为原始数组的第2个元素。
- 求第2个元素到第n个元素的全排列
- 要求第2个元素到第n个元素的全排列，要递归的求第3个元素到第n个元素的全排列......
- 直到递归到第n个元素到第n个元素的全排列，递归出口
- 将改变的数组返回
......
- 不断的改变第一个元素，直至n次for循环中止。
输入: [1,2,3]
输出:[ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]
class Solution {
public:
vector> permute(vector& nums) {
if(!nums.size()){
return res_;
}
vector temp_res;
// used不能用vector，因为值可能会是负数
map used;
backTrace(nums, temp_res, used);
return res_;
}
private:
vector> res_;
void backTrace(vector& nums, vector temp_res, map& used){
if(temp_res.size() == nums.size()){
res_.push_back(temp_res);
return;
}
for(auto num : nums){
if(!used[num]){
used[num] = true;
temp_res.push_back(num);
backTrace(nums, temp_res, used);
temp_res.pop_back();
used[num] = false;
}
}
}
}; 5，求两个数最小公倍数（C++）
最小公倍数=a*b/最大公约数
最大公约数：辗转相除法
6，iou计算，旋转角度的iou计算
这里只讲旋转iou的计算，
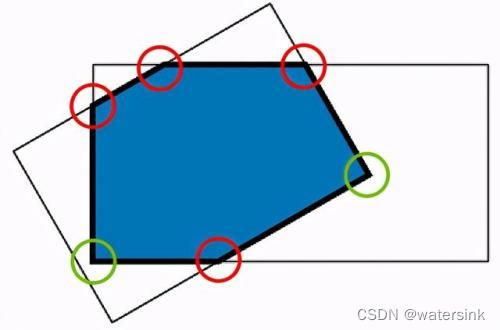
计算两个矩形框的每一条边和另外一个矩形框每一条边的交点，比如其中红色的点，计算每个顶点在是否在另外一个矩形框内部。
最终，交点（红色）和内部的点（绿色）组成一个凸多边形。
然后计算凸多边形面积就可以。
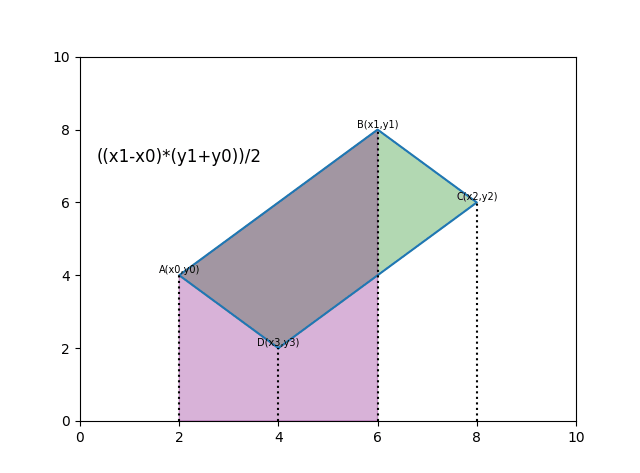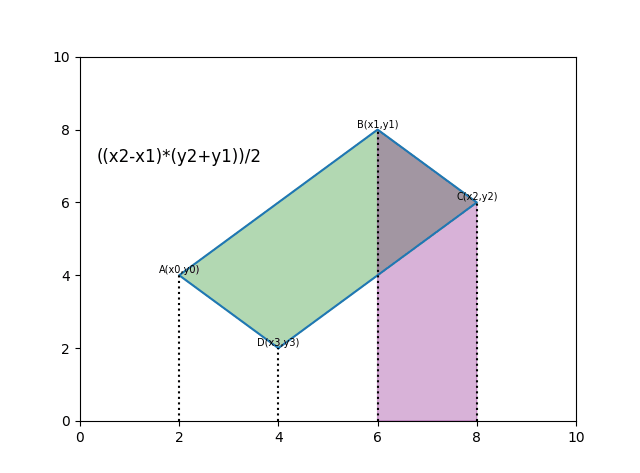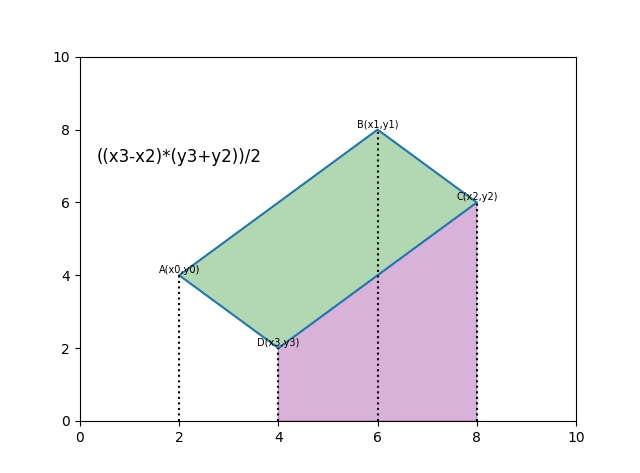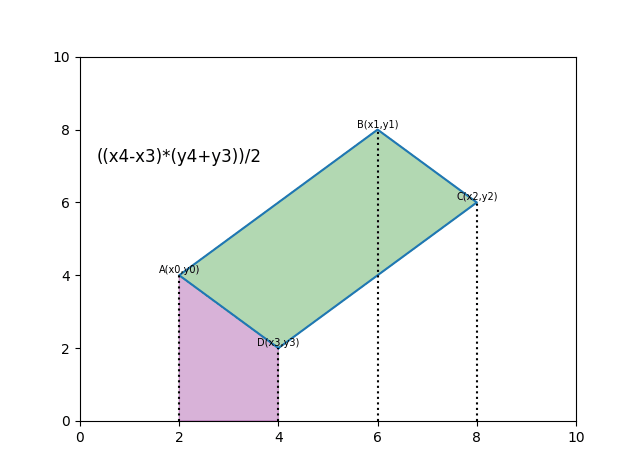
def polygon_area(poly):
'''
compute area of a polygon
:param poly:
:return:
'''
edge = [
(poly[1][0] - poly[0][0]) * (poly[1][1] + poly[0][1]),
(poly[2][0] - poly[1][0]) * (poly[2][1] + poly[1][1]),
(poly[3][0] - poly[2][0]) * (poly[3][1] + poly[2][1]),
(poly[0][0] - poly[3][0]) * (poly[0][1] + poly[3][1])
]
return np.sum(edge)/2.或者，
def polygon_area(x, y):
# Using the shoelace formula
# https://stackoverflow.com/questions/24467972/calculate-area-of-polygon-given-x-y-coordinates
return 0.5 * np.abs(np.dot(x, np.roll(y, 1)) - np.dot(y, np.roll(x, 1)))或者基于opencv计算秃包的面积cv2.contourArea，
6，编辑距离的变种问题，
def editDistance(word1: str, word2: str) -> int:
n1 = len(word1)
n2 = len(word2)
dp = [[0] * (n2 + 1) for _ in range(n1 + 1)]
# init
for j in range(1, n2 + 1):
dp[0][j] = j
for i in range(1, n1 + 1):
dp[i][0] = i
for i in range(1, n1 + 1):
for j in range(1, n2 + 1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1] ) + 1
return dp[-1][-1]7，最大子串和
class Solution {
public int maxSubArray(int[] nums) {
if(nums==null || nums.length<1){
return 0;
}
int cursum=0;
int max=Integer.MIN_VALUE;
for(int i:nums){
if(cursum<=0){
cursum=i;
}
else{
cursum+=i;
}
if(max8，马走日，Knight (象棋马从(0,0)到(n,m)的最小步数)，无限大的棋盘上，马从(0,0) 走到 (x,y)的最小步
解决思路，广度优先搜索bfs，动归dp，贪心greedy
from collections import deque
def solution1(dst):
# BFS
if dst[0] == 0 and dst[1] == 0:
return 0
next = [
(1, 2),
(1, -2),
(2, 1),
(2, -1),
(-1, 2),
(-1, -2),
(-2, 1),
(-2, -1),
]
# (x,y,step), 初始位置为(0,0)，初始步数为0
que = deque([(0, 0, 0)])
while que:
size = len(que)
for _ in range(size):
location = que.popleft()
for i in range(len(next)):
new_location = (location[0] + next[i][0], location[1] + next[i][1], location[2] + 1)
if new_location[0] == dst[0] and new_location[1] == dst[1]:
return new_location[2]
que.append(new_location)
def solution2(dst):
# 动态规划
if dst[0] == 0 and dst[1] == 0:
return 0
x, y = dst
x = abs(x)
y = abs(y)
# 对称
if x > y:
x, y = y, x
# 可参考方法三，将base设置的大一点，dp 转移方程可以写的更简单
base = [
[0, 3, 2],
[3, 2, 1],
[2, 1, 4],
]
if x <= 2 and y <= 2:
return base[y][x]
n = max(x, y) + 1
dp = [[0] * n for _ in range(n)]
for i in range(3):
for j in range(3):
dp[i][j] = base[i][j]
# 对称，y>=x，只遍历下三角矩阵
for i in range(3, n):
for j in range(i + 1):
pre = [dp[i + dy][j + dx]
for dy, dx in [(-1, -2), (-1, 2), (-2, -1), (-2, 1),
# (1, -2), (2, -1), # 遍历下三角矩阵，不需要考虑
]
if 0 <= i + dy < n and 0 <= j + dx < n and dp[i + dy][j + dx] > 0]
dp[i][j] = min(pre) + 1
return dp[y][x]
def solution3(dst):
# 贪心
x, y = dst
x = abs(x)
y = abs(y)
# 此base外面的坐标可以按后面的while 循环缩小
base = [
[0, 3, 2, 3, 2],
[3, 2, 1, 2, 3],
[2, 1, 4, 3, 2],
[3, 2, 3, 2, 3],
[2, 3, 2, 3, 4],
]
if x <= 4 and y <= 4:
return base[y][x]
step = 0
while x > 4 or y > 4:
if x > y:
x, y = y, x
y -= 2
if x == 0:
x += 1
else:
x -= 1
step += 1
if x <= 4 and y <= 4:
break
return step + base[y][x]
import random
import time
t1 = time.time()
for i in range(200):
dst = (int(random.random() * 10), int(random.random() * 10))
# bfs 很慢，这里验证n 设置的小一点
ret1 = solution1(dst)
# 动态规划
ret2 = solution2(dst)
# 贪心
ret3 = solution3(dst)
if ret1 != ret2 or ret1 != ret3:
print(dst, ret1, ret2, ret3)
for i in range(200):
dst = (int(random.random() * 100), int(random.random() * 100))
# 动态规划
ret2 = solution2(dst)
# 贪心
ret3 = solution3(dst)
if ret2 != ret3:
print(dst, ret2, ret3)
print(time.time() - t1)其他，
手写nms，IoU，kmeans
两数求和two sum，三数求和问题three sum
快排
实现任意shape的tensor concat 操作
检查数组对是否可以被 k 整除
有效的括号
打印螺旋矩阵
多数元素（要求一次遍历）
有序数组，目标数的左右边界
字符串数组的打乱的字典序排序
二叉树的右视图
二叉树转双向链表
多个集合的笛卡尔集
编程基础：
1，python修饰器是什么？
- 装饰器可以在不改变原函数代码,不改变原函数调用方式的情况下, 给函数添加扩展功能
- 装饰器的本质就是一个嵌套函数, 如果装饰器需要接收参数, 则需要增加一层函数嵌套
- 装饰器有两种调用方式: 1函数传参方式, 2使用@语法糖
- 装饰器的外层函数接收的是被装饰函数, 返回的是内层函数
- 装饰器的内层函数(即闭包函数)负责装饰被装饰函数
- 装饰器的常用场景有: 打印日志, 性能测试, 权限验证等
2，xrange和range区别
xrange() 函数用法与 range 完全相同，所不同的是生成的不是一个数组，而是一个生成器。
>>>xrange(8)
xrange(8)
>>> list(xrange(8))
[0, 1, 2, 3, 4, 5, 6, 7]
>>> range(8)
[0, 1, 2, 3, 4, 5, 6, 7]3，c++的左值和右值是什么：
- 每个C++表达式生成一个左值或右值
- 如果表达式有一个可以标识的内存地址，则它是左值；否则，是右值
4，单例模式介绍：
单例（Singleton）模式的定义：指一个类只有一个实例，且该类能自行创建这个实例的一种模式。例如，Windows 中只能打开一个任务管理器，这样可以避免因打开多个任务管理器窗口而造成内存资源的浪费，或出现各个窗口显示内容的不一致等错误。
在计算机系统中，还有 Windows 的回收站、操作系统中的文件系统、多线程中的线程池、显卡的驱动程序对象、打印机的后台处理服务、应用程序的日志对象、数据库的连接池、网站的计数器、Web 应用的配置对象、应用程序中的对话框、系统中的缓存等常常被设计成单例。
单例模式有 3 个特点：
（1）单例类只有一个实例对象，通常，普通类的构造函数是公有的，外部类可以通过“new 构造函数()”来生成多个实例。但是，如果将类的构造函数设为私有的，外部类就无法调用该构造函数，也就无法生成多个实例。这时该类自身必须定义一个静态私有实例，并向外提供一个静态的公有函数用于创建或获取该静态私有实例。
（2）该单例对象必须由单例类自行创建；
（3）单例类对外提供一个访问该单例的全局访问点；
5，链表和栈，队列有什么区别：
在链表尾部插入和删除时，就要遍历整个链表来找到尾节点，而在链表头部进行删除和插入操作时只需要根据头指针就可以找到链表的首元素节点
栈作为一种数据结构，只能在一段进行删除或插入操作，所以是先进后出。
队列是一种顺序表，先进先出，在表前段（front）进行删除，尾端（rear）进行插入
6，多进程和多线程有什么区别：
多线程：
高效的内存共享，数据共享；较轻的上下文切换开销；创建销毁切换比较简单。
多进程：
更强的容错性，不会一阻全阻，一个进程崩溃不会整个系统崩溃。更好的多核伸缩性，进程的使用将许多内核资源（如地址空间，页表，打开的文件）隔离，在多核系统上的可伸缩性强于多线程程序
多进程和多线程同样可以提高多核利用率。
其实对于创建和销毁，上下文切换，其实在Linux系统下差别不大，Window下有较大差别。
综上，多进程和多线程的最主要的区别就在资源共享，隔离问题。如果工作使用的内存较大，使用多线程可以避免CPU cache的换入换出，影响性能。
7，python中return和yield有了解吗？
return和yield相同之处：
（1）都用在函数或方法体内。
（2）都用来返回执行的结果。
return和yield不同之处：
return：返回结果后，函数不再继续执行，彻底结束；只执行一次，函数结束
yield：返回结果后，函数不结束，yield返回值后暂停，再次调用时，在暂停的地方继续执行；可执行多次，直到函数结束
8，pytorch基础：说说dataloader()的结构构成与作用？
torch.utils.data.Dataloader
功能：抽象类，所有自定义的Dataset需要继承它，并且复写__getitem__()，__init__(),
getitem：接收一个索引，返回一个样本
init：数据集初始化，读取数据列表，统计数据长度等。
9，torch.nn.Sequential()的作用是什么，torch.nn.ModuleList ()的作用是什么，两者之间有什么区别？
Sequential内部module是有序的，内部已经实现了forward函数，nn.Sequential可以使用OrderedDict对每层进行命名
ModuleList内部module是无序的，需要用户自己写forward函数，module执行的顺序是由forward函数决定的
10，pytorch中detach操作是什么样的，有什么作用？
detach就是把网络中的一部分分量从反向传播的流程中拿出来，使之requires_grad=False
但是拿出来的时候，还是指向原向量的地址，所以对拿出来的向量进行操作的时候，也会影响原向量。
算法：
1，opencv中图像深拷贝和浅拷贝
浅拷贝，是指当图像之间进行赋值时，图像数据并未发生复制，而是两个对象都指向同一块内存块。
深拷贝，是指新创建的图像拥有原始图像的崭新拷贝，即拷贝图像和原始图像在内存中存放在不同地方。
OpenCV中可以通过下面两种方式实现深拷贝：
img.copyTo(img1)
img1=img.clone()2，NMS，softNMS原理
答：NMS：非极大抑制，
- 对所有类别预测的概率值进行排序；并剔除极小概率的框；
- 以第一个框为基准，依次与后面的框进行 IOU 计算，大于 0.5 的框将被剔除；
- 依次对第二个框进行上述操作；
- 最后对每个类别分别进行 NMS；
softNMS:
nms存在两个问题：
- 当两个目标框接近时，分数更低的框就会因为与之重叠面积过大而被删掉
- NMS的阈值需要手动确定，设置小了会漏检，设置大会误检
针对上述两个问题，我们可以不直接删除所有IOU大于阈值的框，而是降低其置信度，即softnms算法原理。
soft nms改进思想是：M为当前得分最高框，bi为待处理框，bi和M的IOU越大，bi的得分si就下降的越厉害（而不是直接置零）。有两种衰减方式，一种是线性加权，一种是高斯加权；
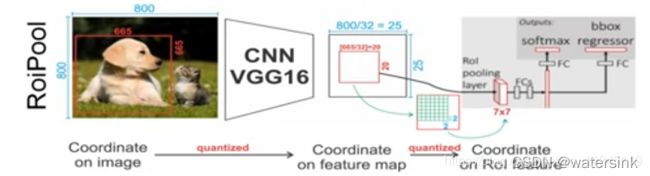
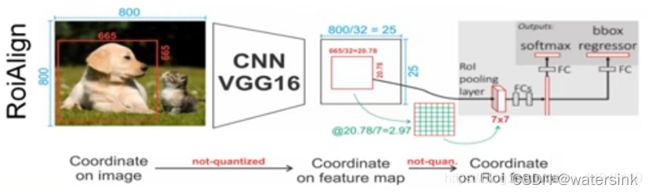
3，ROI pooling（Faster RCNN）和ROI Align（Mask RCNN）有什么区别？
ROI Pooling在faster RCNN中提出。主要有2个缺点，
- 需要进行2次量化取整的操作，会带来精度的损失
- ROI区域中的像素是离散化的，没有梯度的更新，不能进行训练的调节
ROI Align的改进点：
- 改进了ROI pooling中2次量化操作，从而使得精度有保障。
2.对每一个bin内部的N个插值的像素使用双线性插值进行跟新，有梯度的传导
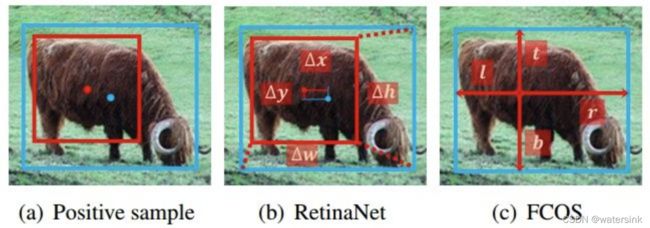
4，Anchor Free和Anchor base回归方式原理和区别？
论文：Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection
Anchor Free（FCOS， ATSS）：point回归，每个点预测距离4条边的距离模式。
Anchor base（RetinaNet）：anchor回归，retinanet那种基于anchor回归的模式（tx,ty,tw,th）。
5，FPN，region proposal时怎么知道roi 是属于哪一个feature map的？
作者将FPN的各个特征层类比为图像金字塔的各个level的特征，从而将不同尺度的RoI映射到对应的特征层上。以224大小的图片输入为例，宽高为w和h的RoI将被映射到的特征级别为k，它的计算公式如下：
在ResNet中，k0的值为4，对应了长宽为224的框所在的层次。如果框的长宽相对于224分别除以2，那么k的值将减1，以此类推。
6，Relu，max pooling，mean pooling，argmax反向传播怎么算？
Relu：
Relu(x) = max(0,x),对于ReLU函数, 当x>0的时候,其导数为1; 当x<0时,其导数为0. 则ReLU函数在x=0的次梯度是 [0,1] ,这里是次梯度有多个,可以取0,1之间的任意值. 工程上为了方便取c=0即可.
max pooling：
不考虑上层回传回来的梯度的话，最大值位置梯度均为1，其余位置梯度为0.
mean pooling：
对于mean pooling，下一层的误差项的值会平均分配到上一层对应区块中的所有神经元。
argmax：
argmax的反向梯度求导跟max pooling有些相似之处，但也有所不同，因为argmax是取出最大值所在的位置
t = torch.tensor([-0.0627, 0.1373, 0.0616, -1.7994, 0.8853,
-0.0656, 1.0034, 0.6974, -0.2919, -0.0456])
torch.argmax(t).item() # outputs 6
strainght through estimator: 假设输入的向量是v, 那么我们用softmax得到softmax(v). 这样, 最大值那个地方就会变得很靠近1, 其他地方就会变得很靠近0. 然后, 我们计算argmax(v), 接着可以得到一个常数c = argmax(v) - softmax(v). 我们这时, 可以用softmax(v) + c来作为argmax(v)的结果. 这个东西的好处是, 我们的softmax(v) + c是有反向传播的能力的. 换句话说, 我们用softmax(v)的梯度来作为反向传播.
7，近年来，一些新的目标检测的backbone有哪些，各有什么特点？
Backbone的改进有以下几个方向：
变深（resnet系列）、
变宽（Inception系列）、
变小（mobile、shuffle等）、
利用特征（densenet、senet等）
针对检测专门设计的backbone（比如darknet）。
8，transformer在多模态数据中的优势?
transformer在多模态领域的强大，是因为它自身的self-attention结构能适应各种不同类型的数据，使得各种数据在模式的对齐上表现更加优秀。
论文：Perceiver: General Perception with Iterative Attention
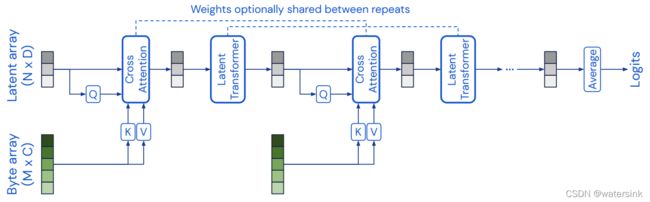用cross attention 迭代的吸收不同模态的数据！
9，为什么要用 weight BCE+dice loss的损失，focal loss 了解吗？
weight BCE:加的权值为β
dice loss:
本质就是不断学习，使得交比并越来越大。
Dice loss = 1.0 - IOU
focal loss:论文中α=0.25，γ=2效果最好。
10，深度学习里的归一化，BN，LN，IN，GN，SN
维度：N,C,H,W
BN：解决训练不稳定的问题，BN将输出从饱和区拉到非饱和区，解决了梯度消失的问题，可以使用大的学习率，加快网络收敛，提供了类似DropOut的正则化作用，减少过拟合
训练的时候：使用当前batch统计的均值和方差对数据进行标准化，同时优化优化gamma和beta两个参数。另外利用指数滑动平均收集全局的均值和方差。
测试的时候：使用训练时收集全局均值和方差以及优化好的gamma和beta进行推理。
LN：LN是针对深度网络的某一层的所有神经元的输入进行normalize操作。
LN中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差
IN：图像风格化中，生成结果主要依赖于某个图像实例，所以对整个batch归一化不适合图像风格化中，因而对HW做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。
GN：主要是针对Batch Normalization对小batchsize效果差，GN将channel方向分group，然后每个group内做归一化，算(C//G)*H*W的均值，这样与batchsize无关，不受其约束。SN：Switchable Normalization，
本篇论文作者认为，
第一，归一化虽然提高模型泛化能力，然而归一化层的操作是人工设计的。在实际应用中，解决不同的问题原则上需要设计不同的归一化操作，并没有一个通用的归一化方法能够解决所有应用问题；
第二，一个深度神经网络往往包含几十个归一化层，通常这些归一化层都使用同样的归一化操作，因为手工为每一个归一化层设计操作需要进行大量的实验。
因此作者提出自适配归一化方法——Switchable Normalization（SN）来解决上述问题。与强化学习不同，SN使用可微分学习，为一个深度网络中的每一个归一化层确定合适的归一化操作。
11，通常有什么数据增强的方法？
翻转，旋转，裁剪，缩放，平移，抖动
Cutout：Improved Regularization of Convolutional Neural Networks with Cutout
Random Erasing：Random Erasing Data Augmentation
Mixup：mixup: BEYOND EMPIRICAL RISK MINIMIZATION
Hide-and-Seek：Hide-and-Seek: A Data Augmentation Technique for Weakly-Supervised Localization and Beyond
CutMix：CutMix: Regularization Strategy to Train Strong Classififiers with Localizable Features
GridMask：GridMask Data Augmentation
FenceMask：FenceMask: A Data Augmentation Approach for Pre-extracted Image Features
KeepAugment：KeepAugment: A Simple Information-Preserving Data Augmentation Approach
SMOTE：该方法来自遥远的2002年。主要应用在小型数据集上来获得新的样本，实现方式是随机选择一个样本，计算它与其它样本的距离，得到K近邻，从K近邻中随机选择多个样本构建出新样本。之所以不提论文中的构建方式，是因为该方法并不是用于图像，但读者可自主设计出图像的构建方式。
Mosaic：该方法来源于YOLO_v4，原理是使用四张图片拼接成一张图片。这样做的好处是图片的背景不再是单一的场景，而是在四种不同的场景下，且当使用BN时，相当于每一层同时在四张图片上进行归一化，可大大减少batch-size。
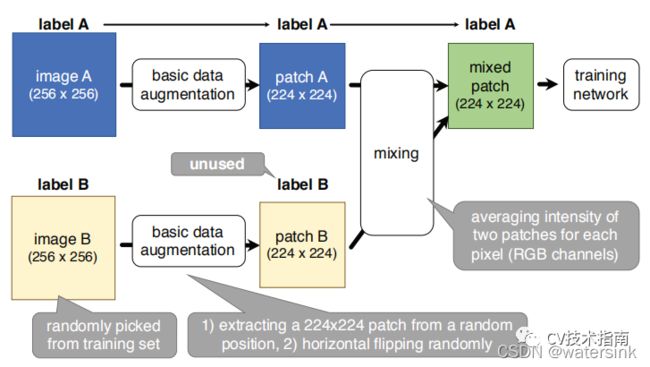
SamplePairing：该方法的原理是从训练集中随机选择两张图片，经过几何变化的增强方法后，逐像素取平均值的方式合成新的样本。具体如下图所示：
12，iou loss介绍
IoU loss：
- 能够很好的反映重合程度
- 具有尺度不变性
- 当不相交时，loss为0
GIoU loss：
A为预测边界框和GT最小外接矩形面积
预测边界框和GT 垂直或水平的时候，退化成IoU
DIoU Loss：
IoU 和GIoU 收敛比较慢，回归的不够准确
DIoU直接最小化两个boxes之间的距离，因此收敛速度更快
CIoU Loss：
Complete-IoU
一个优秀的回归定位损失应该考虑到3种几何参数
重叠面积，中心点距离，长宽比
13，解决难样本问题的方法，ohem与focal loss，asl loss的相同点和不同点
OHEM（online hard example mining）：
OHEM的主要思想可以用原文的一句话概括：
In OHEM each example is scored by its loss, non-maximum suppression (nms) is then applied, and a minibatch is constructed with the highest-loss examples。
OHEM算法虽然增加了错分类样本的权重，但是OHEM算法忽略了容易分类的样本
Focal Loss：
ASL loss：
令
则
MS-COCO，Combined mAP obtained for
14，梯度消失和爆炸的原因和解决方法？（聊的比较深入，主要从反向传播的机制以及sigmoid的导数曲线特征解释为什么会有Relu和resnet这样的方法来解决梯度消失）
原因：
sigmoid函数数学表达式为及其导数为：
可见sigmoid的导数的最大值为1/4，通常初始化的网络权值w通常都小于1，从而有
当
，也就是w比较大的情况。则前面的网络层比后面的网络层梯度变化更快，引起了梯度爆炸的问题。通常来说当激活函数是sigmoid时,梯度消失比梯度爆炸更容易发生。
梯度消失解决方法:
- 预训练加微调
- 梯度剪切、正则
- relu、leakrelu、elu等激活函数
- Batchnorm
- 残差结构
- LSTM
梯度爆炸解决方法:
- 梯度截断clip
- 加正则项，BN，L1，L2
15，ATSS介绍
正负样本的定义和选取对于模型最终效果的影响
自适应的选取正样本的方法
保证了所有正样本anchor都是在groundtruth周围
根据不同层的特征对不同层的正样本的阈值进行了微调
贡献
基于锚点的检测器和不带锚点的检测器的本质区别是如何定义正训练样本和负训练样本
提出自适应训练样本选择，以根据对象的统计特征自动选择正训练样本和负训练样本
证明在图像的每个位置平铺多个锚点以检测对象是没有用的
不引入额外开销的情况下，实现MS COCO的最新性能
具体方法：
1.对于每个输出的检测层，选计算每个anchor的中心点和目标的中心点的L2距离，选取K个anchor中心点离目标中心点最近的anchor为候选正样本（candidate positive samples）
2.计算每个候选正样本和groundtruth之间的IOU，计算这组IOU的均值和方差
3.根据方差和均值，设置选取正样本的阈值：t=m+g ；m为均值，g为方差
4.根据每一层的t从其候选正样本中选出真正需要加入训练的正样本
5.训练
16，dice loss为何能够解决正负样本不平衡问题?
应对语义分割中正负样本强烈不平衡的场景
dice loss 对正负样本严重不平衡的场景有着不错的性能，训练过程中更侧重对前景区域的挖掘。但训练loss容易不稳定，尤其是小目标的情况下。另外极端情况会导致梯度饱和现象。因此有一些改进操作，主要是结合ce loss等改进，比如: dice+ce loss，dice + focal loss等
dice coefficient 源于二分类，本质上是衡量两个样本的重叠部分
为了计算预测的分割图的 dice coefficient, 近似为预测图每个类别score和target的系数
soft dice loss，直接使用预测概率而不是使用阈值或将它们转换为二进制mask
soft dice loss 将每个类别分开考虑，然后平均得到最后结果
在使用DICE loss时，对小目标是十分不利的，因为在只有前景和背景的情况下，小目标一旦有部分像素预测错误，那么就会导致Dice大幅度的变动，从而导致梯度变化剧烈，训练不稳定
i表示像素位置，N表示像素位置总数；c表示类别，m表示类别总数
yic表示类别c在第i个位置的真实像素类别，yic^表示对应的预测概率
17，Mish，swish，GELU对比分析
Mish:
论文：Mish: A Self Regularized Non-Monotonic Neural Activation Function
一种自正则的非单调神经激活函数，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。根据论文实验，该函数在最终准确度上比Swish(+0.494%)和ReLU(+ 1.671%)都有提高。在yolov4中使用（cbl--->cbm）
Swish:
Swish 在深层模型上的效果优于 ReLU。可以看做是介于线性函数与ReLU函数之间的平滑函数.例如，仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%，Inception-ResNet-v 的分类准确率提高 0.6%。
β是个常数或可训练的参数，Swish 具备无上界有下界、平滑、非单调的特性。
GELU:
高斯误差线性单元激活函数在最近的 Transformer 模型（谷歌的 BERT 和 OpenAI 的 GPT-2）中得到了应用。GELU 的论文来自 2016 年，但直到最近才引起关注。
18，梯度下降优化器对比（sgd，adagrad，RMSprop，Adadelta，adam）
SGD，SGDM，Adagrad，RMSProp，Adam，AdamW复习笔记 - 知乎
https://blog.csdn.net/qq_14845119/article/details/86491430
19，训练&测试策略
EMA：
对训练过程的weights进行指数加权平均来提升泛化性能，这个TensorFlow有对应的实现tf.train.ExponentialMovingAverage：
shadow_variable = decay * shadow_variable + (1 - decay) * variableSWA（Stochastic Weight Averaging）:
论文：SWA Object Detection
SWA简单来说就是对训练过程中的多个checkpoints进行平均，以提升模型的泛化性能。记训练过程第i个epoch的checkpoint为wi，一般情况下我们会选择训练过程中最后的一个epoch的模型wn或者在验证集上效果最好的一个模型wi*作为最终模型。但SWA一般在最后采用较高的固定学习速率或者周期式学习速率额外训练一段时间，取多个checkpoints的平均值作为最终模型。
SWA的具体做法如下图所示，前75%的时间使用标准的衰减学习速率策略训练，然后剩余25%设置一个合理的固定学习速率进行训练，最后平均第二阶段每个epoch的weights。如下图b所示，也可以采用在每个epoch采用周期式的学习速率策略来训练。另外一点是模型中如果有BN层，那么应该用SWA得到的模型在训练数据中跑一遍得到BN层的running statistics。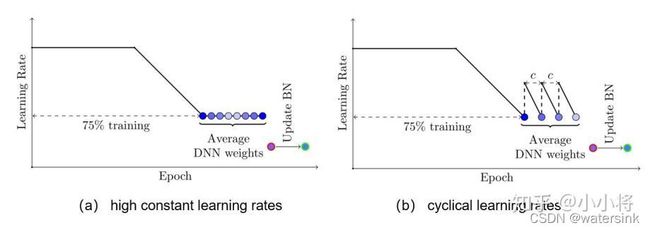 
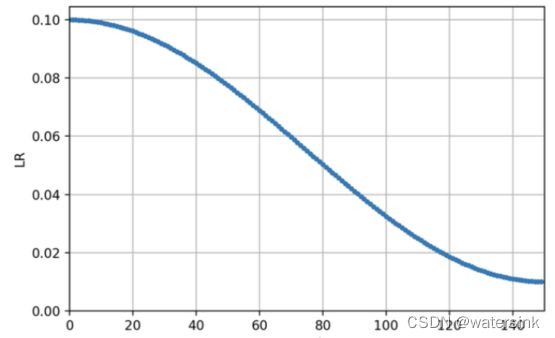
余弦退火（cosine annealing）：
训练时当越来越接近loss值的全局最小值时，学习率应该变得更小来使得模型尽可能接近这一点，而余弦退火可以通过余弦函数来降低学习率。余弦函数中随着x的增加余弦值首先缓慢下降，然后加速下降，再次缓慢下降。这种下降模式能和学习率配合，以一种十分有效的计算方式来产生很好的效果。
梯度累加（gradient accumulation）：
传统的训练函数，一个batch是这么训练的：
for i, (image, label) in enumerate(train_loader):
# 1. input output
pred = model(image)
#获取 loss：输入图像和标签，通过infer计算得到预测值，计算损失函数
loss = criterion(pred, label)
# 2. backward
optimizer.zero_grad() # reset gradient，清空过往梯度
loss.backward()#反向传播，计算当前梯度
optimizer.step()#根据梯度更新网络参数
使用梯度累加是这么写的：
for i,(image, label) in enumerate(train_loader):
# 1. input output
pred = model(image)
#获取 loss：输入图像和标签，通过infer计算得到预测值，计算损失函数
loss = criterion(pred, label)
# 2.1 loss regularization
loss = loss / accumulation_steps
# 2.2 back propagation， 反向传播，计算当前梯度
loss.backward()
#不清空梯度，使梯度累加在已有梯度上
# 3. update parameters of net
if (i+1) % accumulation_steps == 0:
# optimizer the net
optimizer.step() # update parameters of net，根据累计的梯度更新网络参数
optimizer.zero_grad()# reset gradient，清空过往梯度，为下一波梯度累加做准备梯度累加就是，每次获取1个batch的数据，计算1次梯度，梯度不清空，不断累加，累加一定次数后，根据累加的梯度更新网络参数，然后清空梯度，进行下一次循环。
一定条件下，batchsize 越大训练效果越好，梯度累加则实现了 batchsize 的变相扩大，如果accumulation_steps 为 8，则batchsize '变相' 扩大了8倍，是我们这种乞丐实验室解决显存受限的一个不错的trick，使用时需要注意，学习率也要适当放大。
对BN没有影响，BN的估算是在forward阶段就已经完成的，并不冲突，只是accumulation_steps=8和真实的batchsize放大八倍相比，效果自然是差一些，毕竟八倍Batchsize的BN估算出来的均值和方差肯定更精准一些。
TTA（Test-time augmentation）：
论文：Test-time augmentation with uncertainty estimation for deep learning-based medical image segmentation
测试时数据增强，比如分割模型，推理阶段对输入图片做镜像，最后将2个结果进行融合。比如人脸识别模型，也做镜像，最后对2个特征进行融合。
20，实例分割和语义分割的区别？
语义分割(Semantic Segmentation)：就是对一张图像上的所有像素点进行分类。(eg: FCN/Unet/Unet++/...)
实例分割(Instance Segmentation)：可以理解为目标检测和语义分割的结合。(eg: Mask R-CNN/...)相对目标检测的边界框，实例分割可精确到物体的边缘；相对语义分割，实例分割需要标注出图上同一物体的不同个体。
21，目标检测如何优化小目标，给定一个项目场景，聊怎么做？
- anchor重新设计，比如yolo中的kmeans聚类，比如其他网络根据网络结构的下采样率来修改anchor大小。
- 先裁图，再在小图上检测小目标
- 网络深度不要太深，避免小目标卷没了，或者FPN+PAN，BiFPN思想
- 增大网络的输入尺寸大小
- 数据增强，超分，保证小目标被网络有效学习
- Roi pooling---->roi align
- 匹配策略，对于小物体不设置过于严格的 IoU threshold，或者采用atss中的样本匹配策略，从而保证正样本的数量
- Nms---->Soft NMS
- 空洞卷积，保证感受野
22，检测里面，样本类别不平衡如何处理？
- 采样方式OHEM
- 损失函数focal loss, weighted cross entrop
- 数据增强，重采样，gan或者其他方式造数据
23，过拟合是什么？遇到过拟合该怎么办？L1正则和L2正则的区别是什么？为什么能解决过拟合问题？
过拟合:所选模型的复杂度比真模型更高;学习时选择的模型所包含的参数过多,对已经数据预测得很好,但是对未知数据预测得很差的现象.
过拟合一般特点:高方差,低偏差;
解决方法：
- Early stopping
- 数据增强
- 正则化方法，L1，L2，模型权重稀疏，模型变简单
- Dropout
- 减少模型容量，减少网络结构
L1公式：
L2公式： 
L1函数和导数曲线：
L2函数和导数曲线：
L1的梯度始终固定，为1或者-1，而L2的梯度随着权重降低而降低。
加了 L1 正则的话基本上经过一定步数后很可能变为0，而 L2 几乎不可能，因为在值小的时候其梯度也会变小。于是也就造成了 L1 输出稀疏的特性。
24，空洞卷积优缺点？
优点：
增大感受野
缺点：
- The Gridding Effect（所谓的网格效应）,kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的。
- 多次叠加多个具有相同空洞率的卷积核会造成格网中有一些像素自始至终都没有参与运算，不起任何作用，这对于像素级别的预测是不友好的。
- 空洞卷积虽然在参数不变的情况下保证了更大的感受野，但是对于一些很小的物体，本身就不要那么大的感受野来说，这是嫉妒不友好的。
25，模型融合具体实现？
- 多模型投票
- 多模型求平均
- 基于ranking进行加权融合
- Bagging，boosting，stacking
26，fpn相似的特征融合介绍
其中红色，黄色的参数共享。
Faster RCNN中的RPN是通过最后一层的特征来做的。最后一层的特征经过3x3卷积，得到256个channel的卷积层，再分别经过两个1x1卷积得到类别得分和边框回归结果。这里将特征层之后的RPN子网络称之为网络头部（network head）。对于特征层上的每一个点，作者用anchor的方式预设了9个框。这些框本身包含不同的尺度和不同的长款比例。
FPN针对RPN的改进是将网络头部应用到每一个P层。由于每个P层相对于原始图片具有不同的尺度信息，因此作者将原始RPN中的尺度信息分离，让每个P层只处理单一的尺度信息。具体的，对{32^2、64^2、128^2、256^2、512^2}这五种尺度的anchor，分别对应到{P2、P3、P4、P5、P6}这五个特征层上。每个特征层都处理1:1、1:2、2:1三种长宽比例的候选框。P6是专门为了RPN网络而设计的，用来处理512大小的候选框。它由P5经过下采样得到。最终一共15个anchor。
另外，上述5个网络头部的参数是共享的。作者通过实验发现，网络头部参数共享和不共享两种设置得到的结果几乎没有差别。这说明不同层级之间的特征有相似的语义层次。这和特征金字塔网络的原理一致。
27，gan的原理，gan loss设置
Generative Adversarial Networks 是什么：两个神经网络，一个用来做判别，discriminator（D），一个用来做生成generator（G）。
goal-1: 训练D使得D可以对输入图片的真伪进行判别。比如输入真实图片X，则D（x）=real。 若输入是由G产生的图片G（z）则期望D（G（z））=fake。
goal-2: 另一个网络训练G，使得当G输入随机噪声z，可以通过网络产生的图片G（z）可以欺骗到D，从而让D判断满足D（G（z））=real。从分布的角度来说，是期望利用生成的图片G（z）来对原样本x的分布做近似，从而可以欺骗到D。
因此GAN的训练和其他的网络训练不同。之前学习的网络都是针对一个确定网络进行训练，解一个优化问题。GAN是同时训练两个神经网络，训练目标是两个网络达到平衡，这属于是博弈论的概念，解minmax问题，优化的解是Nash平衡点。
实际训练时，生成器和判别器采取交替训练，即先训练 D，然后训练 G，不断往复。
损失函数：
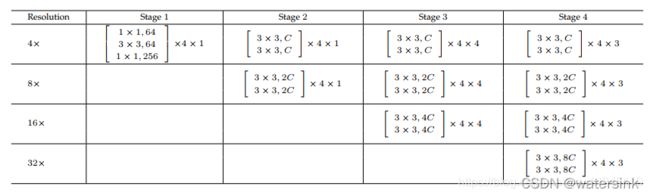
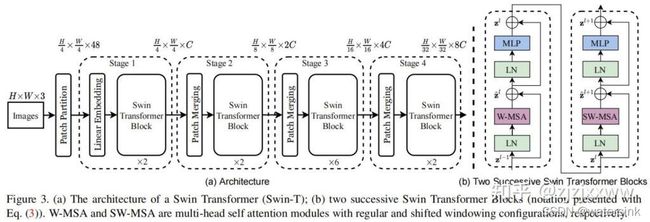
28，Hrnet，efficientnet，swin介绍
Hrnet: 
HRNet从一个高分辨率的卷积干作为第一级开始，逐渐地一个接一个地添加高到低分辨率的分支作为新的级。多分辨率分支并行连接。主体由一系列阶段组成。在每个阶段中，跨分辨率的信息都是反复交换的。
论文一共提出HRNetV1 ，HRNetV2 ，HRNetV2p 共3个基本网络结构。网络整体结构包含4个stage。每一个stage都会进行各个分辨率的特征的融合和输出。其中，刚输出网络的图片，经过stride=2的3*3卷积进行1次下采样，然后每一个stage进行1次下采样。整个网络进行了5次的下采样操作。
Efficientnet：
论文基于深度（depth），宽度（width），输入图片分辨率（resolution）的共同调节，提出了EfficientNets。
MBConv为取反的bootlenet单元，即mobilev2的瓶颈单元。然后将shortcut部分改为se模块。
Swin:
上图是Swin Transformer的整体结构，非常像卷积的层级结构，分辨率每层变成一半，而通道数变成两倍。首先Patch Partition,就是VIT中等分成小块的操作；然后分成4个stage，每个stage中包括两个部分，分别是patch Merging（第一个块是线性层） 和Swin Transformer Block。patch Merging是一个类似于池化的操作，池化会损失信息，patch Merging不会。右图是Swin Transformer Block结构，和transformer block基本类似，不同的地方在多头自注意力MSA换成了窗口多头自注意力W-MSA和移动窗口多头自注意力SW-MSA，右图紫框。
29，Ssd ，yolo，rcnn区别？
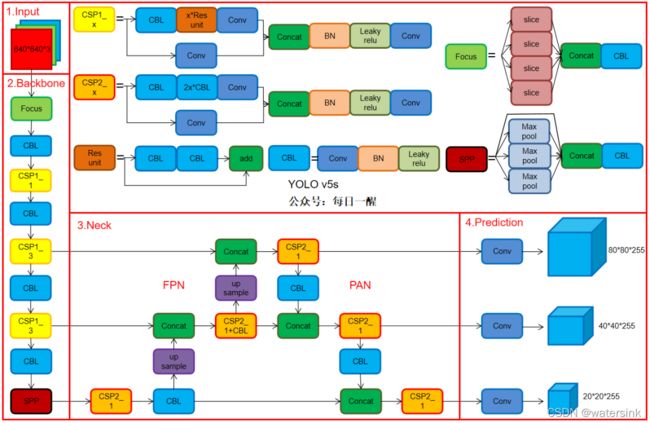
30，Yolov5改进？
- backbone：CSPDarkNet53+Focus
- neck：SPP+PAN
- head：YOLOv3
- 自适应图片缩放
- 数据增强：马赛克（Mosaic）
- 自适应锚框计算
- 激活函数：Leaky ReLU 和 Sigmoid 激活函数。
- 损失函数：GIOU
- 跨网格预测（新的Loss计算方法）
- 消除网格敏感，正负样本匹配等
31，conv底层实现方式
Theano 中的实现：
先把二维 input 展开成一维向量（[in_h, in_w] -> [in_h * in_w]）；如果是一批 inputs，则依次堆叠为一个矩阵 [N, in_h * in_w]；
然后将 kernel 按 stride 循环展开成一个稀疏矩阵；
然后将卷积的计算转化为矩阵相乘。
Caffe 中的实现：
先对 inputs 做 im2col 操作得到输入矩阵，再将 kernel 转化为权值矩阵，然后将两个矩阵相乘得到输出矩阵：
其中
其中 o 表示 out；i 表示 in；k 表示 kernel；不包括 batch_size 的维度；
[o_height, o_width] 的大小由 [i_height, i_width] 及 stride、padding 等参数共同决定。
im2col 操作
先将一个输入矩阵（图像），重叠地划分为多个子矩阵（子区域），对每个子矩阵序列化成向量，然后将所有子向量纵向拼接成另一个矩阵；如果存在多个输入矩阵，则进一步将新生成矩阵横向拼接，最终构成一个大矩阵
32，conv+bn算子融合
33，遥感旋转目标检测
https://github.com/hukaixuan19970627/yolov5_obb
Detecting Rotated Objects Using the NVIDIA Object Detection Toolkit：
Detecting Rotated Objects Using the NVIDIA Object Detection Toolkit | NVIDIA Technical Blog
34，网络训练慢如何定位瓶颈？如何解决dataloader慢？
- 尽量将jpg等格式的文件保存为bmp文件，可以降低解码时间；
- dataloader函数中增加num_workers参数，该参数表示加载数据的线程数，建议设置为该系统中的CPU核心数，可以实现数据的并行读取。
- 异步读取数据，可以考虑使用锁页内存pin_memory，non_blocking实现。
dataloader = data.Dataloader(dataset, batch_size = batch_size, num_workers = workers, pin_memory = True)
for epoch in range(epochs):
for batch_idx, (images, labels) in enumerate(dataloader):
images = images.to(device, non_blocking=True)
labels = labels.to(device, non_blocking=True)35，自定义的cuda op如何验证反向传播的正确性？
使用数值方法计算近似梯度，与自定义ops实现得到的梯度做梯度检查
https://github.com/BVLC/caffe/blob/master/include/caffe/test/test_gradient_check_util.hpp
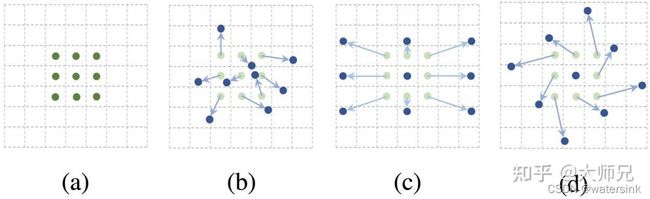
36，DCNV1，DCNV2的原理与实现，感受野的含义
可变形卷积网络（Deformable Convolution Network，DCN）系列算法的提出便是为了增强模型学习复杂的目标不变性的能力。在DCNv1中，作者提出了可变形卷积（Deformable Conv）和可变形池化（Deformable Pooling）两个模块。在DCN v2中，作者为这两个可变形模块添加了权重模块，增强了可变形卷积网络对重要信息的捕捉能力。
DCNv1公式，
使用 △pn 对Feature Map上的一点pn进行扩充，其中 { △pn |n=1,2,......N} ，便是图2上侧我们通过卷积操作预测的卷积核偏移值。
Dcnv1引入了可变形卷积，能更好的适应目标的几何变换。但是v1可视化结果显示其感受野对应位置超出了目标范围，导致特征不受图像内容影响。因此dcnv2
DCNv2公式，
相比v1的改进：
- 增加更多的可变形卷积层，dcnv1在最后三层使用了dcnv1，但是dcnv2在最后的conv3-conv5(12层)都使用了dcov2
- 除了让模型学习采样点的偏移，还要学习每个采样点的权重，这是对减轻无关因素干扰的最重要的工作；
- 提出了特征模拟方案指导网络训练：feature mimicking scheme
37，分析一下SSD,YOLO,Faster rcnn等常用检测网络对小目标检测效果不好的原因？
SSD，YOLO等单阶段多尺度算法，小目标检测需要较高的分辨率，SSD对于高分辨的低层特征没有再利用，而这些层对于检测小目标很重要。按SSD的设计思想，其实SSD对小目标应该有比较好的效果，但是需要重新精细设计SSD中的default box，比如重新设计min_sizes参数，扩大小default box的数量来cover住小目标。但是随着default box数量的增加，网络速度也会降低。
YOLO网络可以理解为是强行把图片分割成7*7个网格，每个网格预测2个目标，相当于只有98个anchor，所以不管是小目标，还是大目标，YOLO的表现都不是很理想，但是由于只需处理少量的anchor，所以YOLO的速度上有很大优势。
Faster rcnn系列对小目标检测效果不好的原因是faster rcnn只用卷积网络的最后一层，但是卷积网络的最后一层往往feature map太小，导致之后的检测和回归无法满足要求。甚至一些小目标在最后的卷积层上直接没有特征点了。所以导致faster rcnn对小目标检测表现较差。
发散题：
1，两个人玩抛硬币的游戏，谁先抛到正面就获胜。那么先抛的人获胜概率为（）。
第一次：正
第三次：反反正
第五次：反反反反正
.......第N次：反反。。。。正
p=1/2+(1/2)^3+(1/2)^5+······+（1/2）^(2n+1)=1/2*(1+1/4+(1/4)^2+……+(1/4)^n)
当公比不为1时，等比数列的求和公式为：
Sn=[a1(1-q^n)]/(1-q)
对于一个无穷递降数列，数列的公比小于1,当上式得n趋向于正无穷大时，分子括号中的值趋近于1，取极限即得无穷递减数列求和公式
S=a1/(1-q)
所以：
2，一条线段，任意分为3段，能组成三角形的概率？
设线段长为a,任意分成三段的长度分别是x 、y 和z=a-(x+y) ,
x +y＜a
三段能构成三角形,则
x+y＞z,即 x+y>(a-x-y),x +y>a/2
y+z＞x,即 y+(a-x-y)>x,x＜a/2
z+x＞y,即 (a-x-y)+x>y,y＜a/2
所求概率等于x+y=a/2、x=a/2、y=a/2三条直线所包围图形的面积除以直线(x+y)=a与x轴、y轴所包围图形的面积（插不了图）.
故将一条线段任意分成三段,这三条线段可以组成一个三角形的概率是
（a/2*a/2*1/2）÷（a*a*1/2）=a²/8÷a²/2=1/4
3，一个班级，存在任意两人或以上生日同一天的概率，要求写出公式
a、50个人可能的生日组合是365×365×365×……×365(共50个)个；
b、50个人生日都不重复的组合是365×364×363×……×316(共50个)个；
c、50个人生日有重复的概率是1-b/a。
这里，50个人生日全不相同的概率是b/a=0.03，因此50个人生日有重复的概率是1-0.03＝0.97，即97%。
反问题就是所有人生日都不一样，答案应该是：1- A(50,365)/365^50=0.97
4，扔鸡蛋不碎的层数（动态规划或数学）
一幢 200 层的大楼，给你两个鸡蛋。如果在第 n 层扔下鸡蛋，鸡蛋不碎，那么从第 n-1 层扔鸡蛋，都不碎。这两只鸡蛋一模一样，不碎的话可以扔无数次。最高从哪层楼扔下时鸡蛋不会碎？
递推关系大概是，当前需要扔一次所以加1。当前这一次可能是从1到n层的任意一层扔下，在n种情况中选择扔的次数最少的。当前这一次扔下，如果鸡蛋碎了，就只用试i-1层，鸡蛋剩下m-1个，如果鸡蛋没碎，就试剩下的n-i层，两种情况中取最大的，因为是最差情况。
至于100层时用14+13+12+……+1，大概是第一次选14层，如果鸡蛋碎了，就只能从第一层开始一层一层往上试，最坏情况下一共14次，如果没碎，第二次选14+13=27层，如果碎了，最坏情况下就从15层一直试到26层，一共也是14次，如果没碎，第三次再从27+12=39层试，以此类推……
import functools
@functools.lru_cache(maxsize=None)
def f(n, m):
if n == 0:
return 0
if m == 1:
return n
ans = min([max([f(i - 1, m - 1), f(n - i, m)]) for i in range(1, n + 1)]) + 1
return ans
print(f(100, 2)) # 14
print(f(200, 2)) # 20项目经验：
1，假设3000w的人脸库，人脸识别系统搭建？
要考虑的问题
向量化检索，使用Elestricsearch（6台120G内存）或者faiss，milvus，增删改查的支持，分布式支持，目前只支持入库（平均一天入库200w的量），查找（top100结果毫秒级别响应）。
向量备份，hbase
特征：cnn特征（128维度）+sift特征（特征点+描述子+FLANN特征匹配）
服务挂掉如何解决，分布式问题
2，换脸的流程？
3，最美证件照流程？
项目内容包括：
- 整体算法流程，包括拦截，人像对齐，抠图换背景，智能换装，一键美颜，清晰度优化，规格对齐
- 使用 MODNet 人像抠图结果，和人像语义分割结果，进行融合，得到最终的 alpha 通道
- 根据脖子关键点和下巴关键点，分区域构建变形映射矩阵，实现智能换装衣服变形和对齐
- 根据脖子是否遮挡，确定智能换装脖子逻辑，如果脖子遮挡严重，使用参考模板图的脖子进行换装，如果脖子未遮挡或遮挡不严重，使用用户图的脖子进行换装
- 参考图脖子进行换装的情况下，使用 LAB 颜色空间，实现脖子颜色迁移，以使其和用户人脸肤色和谐
- 用户图脖子进行换装的情况下，如果换装后脖子有遮挡，计算待修复区域，修改该区域背景，之后使用 CR-Fill 进行修复（https://github.com/zengxianyu/crfill）
- 根据披发分类模型，结合语义分割结果，按需进行头发拉伸变形，实现对应的变形映射矩阵，使用 remap 完成变形
- 使用向量化以及 scipy cdist 优化一键美颜瘦脸 idw 算法，后使用 pytorch 实现该算法，耗时从 40s → 30ms
- 重新实现 opencv warpaffine，以支持 INTER_AREA 插值，按需使用，多次对齐，优化流程，减少清晰度流失
- 使用人脸盲复原模型 GFPGAN（https://github.com/TencentARC/GFPGAN），优化人脸清晰度，解决转 onnx 过程中遇到的问题，使用 triton inference server 进行部署
- 使用图像超分模型 Real-ESRGAN（https://github.com/xinntao/Real-ESRGAN），优化背景清晰度，并转 onnx，使用 triton inference server 进行部署
写在最后：
物有本末，事有始终，知所先后，则近道矣。