【自动驾驶】基于采样的路径规划算法——PRM（含python实现）

参考资料

• 路径规划 | 随机采样算法
• 路径规划: PRM 路径规划算法
• Probabilistic Roadmaps (PRM)
• Probabilistic roadmap

1. 基本概念

1.1 基于随机采样的路径规划算法

• 基于随机采样的路径规划算法适用于高维度空间，它们以概率完备性(当时间接近无限时一定有解)来代替完备性，从而提高搜索效率。

• 基于随机采样的路径规划算法又分为单查询算法(single-query path planning)以及渐近最优算法(asymptotically optimal path planning)，前者只要找到可行路径即可，侧重快速性，后者还会对找到的路径进行逐步优化，慢慢达到最优，侧重最优性。单查询方法包括概率路图算法(Probabilistic Road Map, PRM)、快速随机扩展树算法(Rapidly-exploring Random Tree, RRT)、RRT-Connect算法等，渐近最优算法有RRT*算法等。

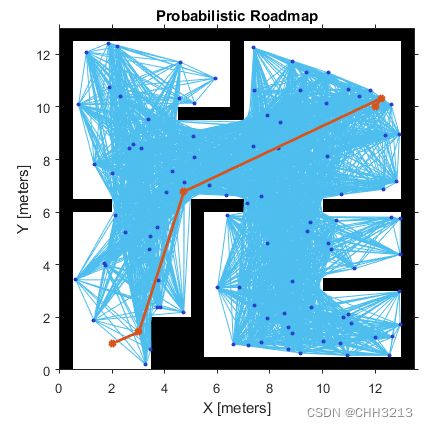
1.2 概率路图算法(Probabilistic Road Map, PRM)

概率路图算法是一种典型的基于采样的路径规划方法。它主要分为两个阶段：学习阶段， 查询阶段。

学习阶段

应用PRM算法进行路径规划时，首先在将连续空间转换成离散空间后，在离散空间中采样一个无碰撞的点（随机撒点，剔除落在障碍物上的点），以该点为中心，在一定的半径范围内搜索其邻域点，并将其连接形成路径，随后进行碰撞检测，若无碰撞，则保留该路径。

查询阶段

当空间中所有采样点均完成上述步骤后，再应用图搜索算法搜索出可行路径。

1.3 PRM算法的优缺点

优点

该算法原理简单，容易实现，只需要调整参数即可实现不同场景的路径规划，且不需要对环境中的障碍物进行精确建模，在高维空间和动态环境中的路径规划有很大优势。

缺点

但该算法存在狭窄通路问题： 空白区域采样点密集，障碍物密集处采样点又相对较少，可能无法得到最短路径。而且参数的设置对路径规划的结果影响较大，采样点的数量、邻域的大小设置不合理均可能导致路径规划失败（如采样点设置过少导致生成的路径过少未覆盖起终点、邻域设置过大导致过多的路径无法通过碰撞检测）。

所以PRM是概率完备且不最优的算法。

1.4 PRM算法伪代码

概率路图的构建过程的伪代码如下：

如上图所示，

• 步骤 1、2 : 初始化两个集合，其中$V$表示随机点集，$E$表示路径集。

• 步骤 3~8 : 每次随机采样一个无碰撞的点，将这个无碰撞的点加入$V$中，重复$n$次。

• 步骤 9~16：生成概率路图。

  • 步骤 10：对$V$中的每个点$q$，根据一定的距离范围选择$k$个邻域点
  • 步骤 11~15：对每个领域点$q^{\prime }$进行判断，如果$q$和$q^{\prime }$尚未形成路径，则将其连接形成路径，随后进行碰撞检测，若无碰撞，则保留该路径。

在依据上述步骤构建完路图后，使用图搜索算法(如Dijkstra算法)在路图中搜索出一条从起点到终点的最短路径即可。

2. python代码实现

代码主体来自pythonRobotics，这里只进行了相应的注释。另外欢迎访问我的github仓库~~

import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
from celluloid import Camera  # 保存动图时用，pip install celluloid

# parameter
N_SAMPLE = 500  # 采样点数目，即随机点集V的大小
N_KNN = 10  # 一个采样点的领域点个数
MAX_EDGE_LEN = 30.0  # [m] Maximum edge length

show_animation = True

"""
kd-tree用于快速查找nearest-neighbor

query(self, x[, k, eps, p, distance_upper_bound]): 查询kd-tree附近的邻居


"""

class Node:
    """
    Node class for dijkstra search
    """

    def __init__(self, x, y, cost, parent_index):
        self.x = x
        self.y = y
        self.cost = cost # 每条边权值
        self.parent_index = parent_index

    def __str__(self):
        return str(self.x) + "," + str(self.y) + "," +\
            str(self.cost) + "," + str(self.parent_index)


def prm_planning(start_x, start_y, goal_x, goal_y, obstacle_x_list, obstacle_y_list, robot_radius, *, camara=None,rng=None):
    """
    Run probabilistic road map planning

    :param start_x: start x position
    :param start_y: start y position
    :param goal_x: goal x position
    :param goal_y: goal y position
    :param obstacle_x_list: obstacle x positions
    :param obstacle_y_list: obstacle y positions
    :param robot_radius: robot radius
    :param rng: 随机数构造器
    :return:
    """
    obstacle_kd_tree = KDTree(np.vstack((obstacle_x_list, obstacle_y_list)).T)
    # 采样点集生成
    sample_x, sample_y = sample_points(start_x, start_y, goal_x, goal_y,
                        robot_radius,
                        obstacle_x_list, obstacle_y_list,
                        obstacle_kd_tree, rng)
    if show_animation:
        plt.plot(sample_x, sample_y, ".b")

    # 生成概率路图
    road_map = generate_road_map(sample_x, sample_y, robot_radius, obstacle_kd_tree)
    # 使用迪杰斯特拉规划路径
    rx, ry = dijkstra_planning(
        start_x, start_y, goal_x, goal_y, road_map, sample_x, sample_y,camara)

    return rx, ry


def is_collision(sx, sy, gx, gy, rr, obstacle_kd_tree):
    """判断是否发生碰撞,true碰撞，false不碰
        rr: 机器人半径
    """
    x = sx
    y = sy
    dx = gx - sx
    dy = gy - sy
    yaw = math.atan2(gy - sy, gx - sx)
    d = math.hypot(dx, dy)

    if d >= MAX_EDGE_LEN:
        return True

    D = rr
    n_step = round(d / D)

    for i in range(n_step):
        dist, _ = obstacle_kd_tree.query([x, y])  # 查询kd-tree附近的邻居
        if dist <= rr:
            return True  # collision
        x += D * math.cos(yaw)
        y += D * math.sin(yaw)

    # goal point check
    dist, _ = obstacle_kd_tree.query([gx, gy])
    if dist <= rr: 
        return True  # collision

    return False  # OK


def generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree):
    """
    概率路图生成

    sample_x: [m] x positions of sampled points
    sample_y: [m] y positions of sampled points
    robot_radius: Robot Radius[m]
    obstacle_kd_tree: KDTree object of obstacles
    """

    road_map = []
    n_sample = len(sample_x)
    sample_kd_tree = KDTree(np.vstack((sample_x, sample_y)).T)

    for (i, ix, iy) in zip(range(n_sample), sample_x, sample_y):
        # 对V中的每个点q，选择k个邻域点
        dists, indexes = sample_kd_tree.query([ix, iy], k=n_sample)
        edge_id = []

        for ii in range(1, len(indexes)):
            nx = sample_x[indexes[ii]]
            ny = sample_y[indexes[ii]]
            # 对每个领域点$q'$进行判断，如果$q$和$q'$尚未形成路径，则将其连接形成路径并进行碰撞检测，若无碰撞，则保留该路径。
            if not is_collision(ix, iy, nx, ny, rr, obstacle_kd_tree):
                edge_id.append(indexes[ii])

            if len(edge_id) >= N_KNN:
                break

        road_map.append(edge_id)

    #  plot_road_map(road_map, sample_x, sample_y)

    return road_map


def dijkstra_planning(sx, sy, gx, gy, road_map, sample_x, sample_y,camara):
    """
    s_x: start x position [m]
    s_y: start y position [m]
    goal_x: goal x position [m]
    goal_y: goal y position [m]
    obstacle_x_list: x position list of Obstacles [m]
    obstacle_y_list: y position list of Obstacles [m]
    robot_radius: robot radius [m]
    road_map: 构建好的路图 [m]
    sample_x: 采样点集x [m]
    sample_y: 采样点集y [m]

    @return: Two lists of path coordinates ([x1, x2, ...], [y1, y2, ...]), empty list when no path was found
    """

    start_node = Node(sx, sy, 0.0, -1)
    goal_node = Node(gx, gy, 0.0, -1)
    # 使用字典的方式构造开闭集合
    # openList表由待考察的节点组成， closeList表由已经考察过的节点组成。
    open_set, closed_set = dict(), dict()
    open_set[len(road_map) - 2] = start_node

    path_found = True
    # 步骤与A星算法一致
    while True:
        # 如果open_set是空的
        if not open_set:
            print("Cannot find path")
            path_found = False
            break

        c_id = min(open_set, key=lambda o: open_set[o].cost)
        current = open_set[c_id]

        # show graph
        if show_animation and len(closed_set.keys()) % 2 == 0:
            # for stopping simulation with the esc key.
            plt.gcf().canvas.mpl_connect(
                'key_release_event',
                lambda event: [exit(0) if event.key == 'escape' else None])
            plt.plot(current.x, current.y, "xg")
            plt.pause(0.001)
            if camara !=None:
                camara.snap()

        if c_id == (len(road_map) - 1):
            print("goal is found!")
            goal_node.parent_index = current.parent_index
            goal_node.cost = current.cost
            break

        # Remove the item from the open set
        del open_set[c_id]
        # Add it to the closed set
        closed_set[c_id] = current

        # expand search grid based on motion model
        for i in range(len(road_map[c_id])):
            n_id = road_map[c_id][i]
            dx = sample_x[n_id] - current.x
            dy = sample_y[n_id] - current.y
            d = math.hypot(dx, dy)
            node = Node(sample_x[n_id], sample_y[n_id],
                        current.cost + d, c_id)

            if n_id in closed_set:
                continue
            # Otherwise if it is already in the open set
            if n_id in open_set:
                if open_set[n_id].cost > node.cost:
                    open_set[n_id].cost = node.cost
                    open_set[n_id].parent_index = c_id
            else:
                open_set[n_id] = node

    if path_found is False:
        return [], []

    # generate final course
    rx, ry = [goal_node.x], [goal_node.y]
    parent_index = goal_node.parent_index
    while parent_index != -1:
        n = closed_set[parent_index]
        rx.append(n.x)
        ry.append(n.y)
        parent_index = n.parent_index

    return rx, ry


def sample_points(sx, sy, gx, gy, rr, ox, oy, obstacle_kd_tree, rng):
    """采样点集生成
    """
    max_x = max(ox)
    max_y = max(oy)
    min_x = min(ox)
    min_y = min(oy)

    sample_x, sample_y = [], []

    if rng is None:
        rng = np.random.default_rng()

    while len(sample_x) <= N_SAMPLE:
        tx = (rng.random() * (max_x - min_x)) + min_x
        ty = (rng.random() * (max_y - min_y)) + min_y

        # 在障碍物中查询离[tx, ty]最近的点的距离
        dist, index = obstacle_kd_tree.query([tx, ty])

        # 距离大于机器人半径，说明没有碰撞，将这个无碰撞的点加入V中，重复n次。
        if dist >= rr:
            sample_x.append(tx)
            sample_y.append(ty)
    # 别忘了起点和目标点
    sample_x.append(sx)
    sample_y.append(sy)
    sample_x.append(gx)
    sample_y.append(gy)

    return sample_x, sample_y


def plot_road_map(road_map, sample_x, sample_y):  # pragma: no cover

    for i, _ in enumerate(road_map):
        for ii in range(len(road_map[i])):
            ind = road_map[i][ii]

            plt.plot([sample_x[i], sample_x[ind]],
                     [sample_y[i], sample_y[ind]], "-k")

def main(rng=None):
    print( " start!!")
    fig = plt.figure(1)

    # camara = Camera(fig)  # 保存动图时使用
    camara = None
    # start and goal position
    sx = 10.0  # [m]
    sy = 10.0  # [m]
    gx = 50.0  # [m]
    gy = 50.0  # [m]
    robot_size = 5.0  # [m]

    ox = []
    oy = []

    for i in range(60):
        ox.append(i)
        oy.append(0.0)
    for i in range(60):
        ox.append(60.0)
        oy.append(i)
    for i in range(61):
        ox.append(i)
        oy.append(60.0)
    for i in range(61):
        ox.append(0.0)
        oy.append(i)
    for i in range(40):
        ox.append(20.0)
        oy.append(i)
    for i in range(40):
        ox.append(40.0)
        oy.append(60.0 - i)

    if show_animation:
        plt.plot(ox, oy, ".k")
        plt.plot(sx, sy, "^r")
        plt.plot(gx, gy, "^c")
        plt.grid(True)
        plt.axis("equal")
        if camara != None:
            camara.snap()

    rx, ry = prm_planning(sx, sy, gx, gy, ox, oy, robot_size,camara=camara, rng=rng)

    assert rx, 'Cannot found path'

    if show_animation:
        plt.plot(rx, ry, "-r")
        plt.pause(0.001)
        if camara!=None:
            camara.snap()
            animation = camara.animate()
            animation.save('trajectory.gif')
        plt.savefig("result.png")
        plt.show()


if __name__ == '__main__':
    main()

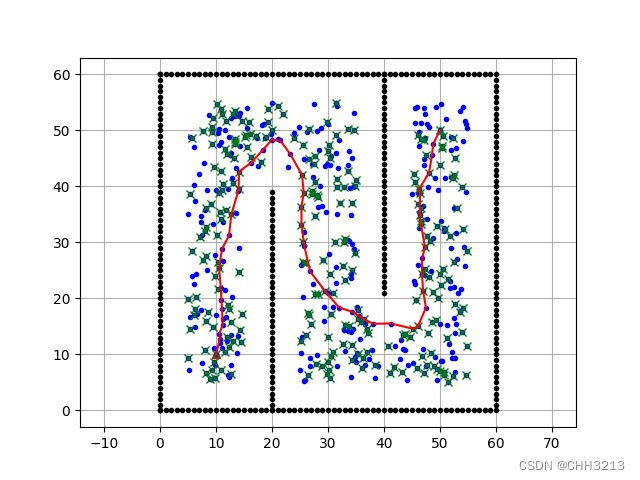
实现效果如下：