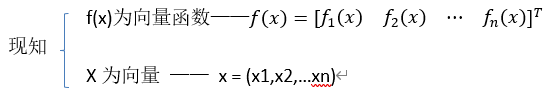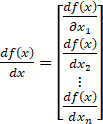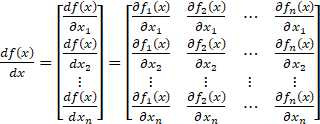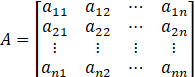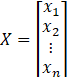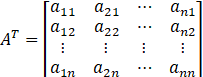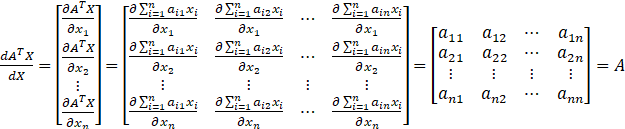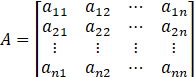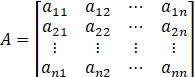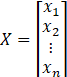- 14.3 FFT与PEFT终极对决:1%参数实现3倍速训练,显存暴降80%!
少林码僧
掌握先机!从0起步实战AI大模型微调打造核心竞争力人工智能机器学习大数据语言模型chatgptllama
以微调权重比例分类:FFTvsPEFT深度解析在大模型微调领域,参数调整比例直接决定训练效率与模型性能的平衡。本小节将深入解析全参数微调(FullFine-Tuning,FFT)与参数高效微调(Parameter-EfficientFine-Tuning,PEFT)的核心差异,并通过具体技术方案对比和实战代码示例揭示其工程应用场景。一、FFT与PEFT技术对比矩阵
- VSCode使用Jupyter完整指南配置机器学习环境
z日火
校招学习日记vscodejupyter机器学习
接下来开始机器学习部分第一步配置环境:VSCode使用Jupyter完整指南1.安装必要的扩展打开VSCode,按Ctrl+Shift+X打开扩展市场,搜索并安装以下扩展:必装扩展:Python(Microsoft官方)-Python语言支持Jupyter(Microsoft官方)-Jupyternotebook支持Pylance(Microsoft官方)-Python智能提示和语法检查推荐扩展:
- 养老院管理系统基于SpringBoot的养老院管理系统系统设计与实现(源码+论文+部署讲解等)
博主介绍:✌全网粉丝60W+,csdn特邀作者、Java领域优质创作者、csdn/掘金/哔哩哔哩/知乎/道客/小红书等平台优质作者,计算机毕设实战导师,目前专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌技术栈范围:SpringBoot、Vue、SSM、Jsp、HLMT、Nodejs、Python、爬虫、数据可视化、小程序、安卓app、大数据、物联网、机器学习、单片机
- 锚定“好用”!诚迈科技重磅发布五大信创产品矩阵,共建自主共赢生态
CSDN资讯
信创操作系统数据库人工智能
7月18日,CXC2025诚迈信创生态大会在南京盛大举行。本次大会以“信创大业自主共赢”为主题,主管单位、专家学者、行业领军企业、合作伙伴及媒体齐聚一堂,共同见证诚迈科技重磅发布五大信创产品矩阵,包括面向党政、企业、教育、医疗领域的信创产品以及鸿志操作系统系列产品。会上,诚迈科技携手行业伙伴发起成立信创共赢生态联盟,共同推动产业链协同创新和自主生态繁荣发展。中国电子工业标准化技术协会信息技术应用创
- AI产品经理成长记《零号列车》第一集 邂逅0XAI列车
黑客思维者
AI产品经理养成人工智能AI产品经理大模型智能体
《零号列车》绝非传统意义上的AI产品经理教程——它是我沉淀二十多年跨行业数字化转型与工业4.0实战经验后,首创的100集大型小说体培养指南。那些曾在千行百业验证过的知识与经验,不再是枯燥的文字堆砌,而是化作一场沉浸式的学习旅程。这里没有生硬的理论灌输,而是用跌宕起伏的故事情节,串联起AI技术的底层逻辑。你会跟着角色的脚步推进剧情,在不知不觉中吃透机器学习、大模型应用等专业概念;更有深入浅出的技术拆
- 人工智能时代下的数据新职业:新兴工作岗位版图研究
司南锤
economics人工智能
目录摘要第一章:AI驱动的数据价值链重构1.1从“沉睡金矿”到“流动的血液”:数据作为核心经济资产的激活1.2知识的新经济学:零边际成本革命1.3AI作为新的“操作系统”:重塑产业竞争格局第二章:基石层:数据准备与质量保障中的角色2.1数据标注与标签领导力:数据标注经理/主管2.2“地面真实”的守护者:AI数据质量专家第三章:技术核心层:构建AI与机器学习全生命周期的工程角色3.1AI生产线架构师
- Python领域制造业的Python应用
Python编程之道
Python编程之道python开发语言ai
Python在制造业中的应用:从自动化到智能制造关键词:Python、制造业、工业自动化、数据分析、机器学习、物联网、智能制造摘要:本文深入探讨Python编程语言在制造业中的广泛应用。从基础的自动化脚本到复杂的智能制造系统,Python凭借其丰富的库生态系统和易用性,正在重塑现代制造业。我们将分析Python在制造业中的核心应用场景,包括设备监控、质量控制、预测性维护和供应链优化等,并通过实际案
- 【机器学习】探索未来科技的前沿:人工智能、机器学习与大模型
AIGC零基础入门小白
AI大模型大模型教程人工智能机器学习科技AI大模型AIGCAI教程大模型教程
文章目录引言一、人工智能:从概念到现实1.1人工智能的定义1.2人工智能的发展历史1.3人工智能的分类1.4人工智能的应用二、机器学习:人工智能的核心技术2.1机器学习的定义2.2机器学习的分类2.3机器学习的实现原理2.4机器学习的应用2.5机器学习的示例代码2.6解释代码三、大模型:推动AI前沿发展的关键技术3.1大模型的定义3.2大模型的发展历程3.3深度学习与神经网络3.4大模型的优势与挑
- 2024 睿抗机器人开发者大赛CAIP-编程技能赛-本科组(省赛)RC-u3题解
EarthOnline玩家
机器人java开发语言
题目:暖炉与水豚源题目地址:https://pintia.cn/problem-sets/1813039306479005696/exam/problems/type/7?problemSetProblemId=1813039385617129474问题描述给定一个N×M的矩阵,包含水豚(‘c’表示冷,‘w’表示暖)、暖炉(‘m’)和空格(’.’)。暖炉可以温暖其3×3范围内的水豚。题目保证最多只
- 人工智能入门指南:从基础概念到实际应用
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。https://www.captainbed.cn/north文章目录1.**人工智能的基本概念**1.1什么是人工智能?1.2人工智能的分类2.**人工智能的核心技术**2.1机器学习(MachineLearning)2.1.1机器学习的类型2.1.2机器学习流程2.2深度学习(DeepLearni
- 矩阵A+B(矩阵相加)
crystaljy
矩阵
Description在数学中,矩阵是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实
- Java与机器学习的邂逅:Weka框架入门指南
墨夶
Java学习资料1java机器学习数据挖掘
在这个数据驱动的时代,机器学习已经成为各行业创新和优化的关键技术。而Java,作为一门成熟且广泛应用的编程语言,在企业级应用开发中占据着重要地位。将二者结合起来,利用Java实现机器学习算法,不仅可以充分发挥其强大的生态系统优势,还能为开发者提供一个高效、稳定的开发环境。今天,我们将带您走进Java与机器学习的世界,探索如何使用Weka这一著名的机器学习库来开启您的智能之旅。Weka简介及其优势什
- Java 二维数组详解:从基础语法到实战应用,彻底掌握多维数据结构
大葱白菜
java合集开发语言java后端学习个人开发
作为一名Java开发工程师,你一定在实际开发中遇到过需要处理表格、矩阵、图像像素、游戏地图等场景。这时候,二维数组(2DArray)就派上用场了。本文将带你全面掌握:Java中二维数组的定义与初始化方式二维数组的内存结构与访问机制二维数组的遍历、修改与扩容技巧二维数组在实际业务中的应用场景二维数组与集合类(如List>)的互转常见误区与最佳实践并通过丰富的代码示例和真实项目场景讲解,帮助你写出更高
- 机器学习基础:从数据到智能的入门指南
一、何谓机器学习在我们的日常生活中,机器学习的身影无处不在。当你打开购物软件,它总能精准推荐你可能喜欢的商品;当你解锁手机,人脸识别瞬间完成;当你使用语音助手,它能准确理解你的指令。这些背后,都离不开机器学习的支撑。机器学习是一门让计算机能够从数据中学习并改进的学科。随着传感器技术的飞速发展,我们身边充满了各种传感器,如手机中的摄像头、麦克风,交通监控中的传感器等,它们收集了海量的数据。这些数据就
- 华为OD 面试手撕真题目录
无限码力
华为OD面试手撕代码真题合集华为od面试华为OD面试手撕真题
华为OD面试手撕真题目录,收集的都是实际面试出现过的手撕代码真题,对于是力扣原题的我会在对应题目博客中给出对应对应链接,推荐自己写代码去通过。华为OD机试2025B卷真题题库目录|机考题库+算法考点详解目录序号题目名称考点1求1-n的最小公倍数数学原理2判断是IPV4还是IPV6字符串、模拟3旋转矩阵模拟4
- 2018-08-27
wuwenjuan
《新形势下的智慧新商业矩阵》,李洋老师《行形势下的智慧新商业矩阵》全新出炉,给你全新的颠覆性的智慧新零售商业模式新体验!
- python:numpy分享(保姆级教程)
苏苏susuus
pythonnumpy开发语言
目录一、概念二、相关属性三、ndarray及其实例创建(一)ndarray介绍(二)zeros()、ones()、empty()函数(三)**arange(),**类似python的range(),创建一个一维ndarray数组。(四)**matrix()**,是ndarray的子类,只能生成2维的矩阵(五)rand()、randn()、randint()、uniform()(都是numpy.ra
- 大模型算法工程师技术路线全解析:从基础到资深的能力跃迁
Mr.小海
大模型算法数据挖掘人工智能机器学习深度学习机器翻译web3
文章目录大模型算法工程师技术路线全解析:从基础到资深的能力跃迁一、基础阶段(0-2年经验):构建核心知识体系与工程入门数学与机器学习基础编程与深度学习框架NLP与Transformer入门二、进阶阶段(2-4年经验):深化模型技术与工程落地能力大模型预训练与微调技术预训练原理:数据与任务的协同设计微调工具:参数高效适配与工程优化对齐实践:价值观优化与实证效果分布式训练与框架工具并行策略:多维度协同
- Go与Python在数据管道与分析项目中的抉择:性能与灵活性的较量
真智AI
人工智能pythongo
你正在设计一个全新数据管道或启动一个分析项目,此时你或许正在思考该选择Python还是Go。五年前,这甚至不是个值得讨论的问题——你会毫不犹豫地选择Python,故事到此为止。然而,近年来Go在数据领域,尤其是在数据基础设施和实时处理方面,正逐渐被更多人采用。实际上,这两种语言都已在现代数据技术栈中找到了各自的定位。Python依然非常适合机器学习和数据分析,而Go则逐步成为高性能数据基础设施的首
- Python爬虫实战:从新浪财经爬取股票新闻的完整实现
Python爬虫项目
python爬虫开发语言数据分析php
第一部分:爬虫概述1.1什么是爬虫?爬虫是指通过程序模拟浏览器的行为,自动化地抓取网络上的数据。通过爬虫技术,能够从各种网站上提取信息,广泛应用于数据采集、数据分析、机器学习等领域。1.2新浪财经简介新浪财经是中国最大的财经信息平台之一,提供股票、基金、债券、外汇等多方面的财经新闻和数据。在股票领域,新浪财经提供了大量的股票行情、实时数据、新闻报道等信息,因此爬取新浪财经的股票新闻对于投资分析和决
- AI 智能运维,重塑大型企业软件运维:从自动化到智能化的进阶实践
AI、少年郎
人工智能运维自动化
一、引言:企业软件运维的智能化转型浪潮在数字化转型加速的背景下,大型企业软件架构日益复杂,微服务、多云环境、分布式系统的普及导致传统运维模式面临效率瓶颈。AI技术的渗透催生了智能运维(AIOps)的落地,通过机器学习、大模型、智能Agent等技术,实现从"人工救火"到"智能预防"的范式转变。本文结合头部企业实践,解析AI在运维领域的核心应用场景、技术架构及未来趋势,特别针对基础运维中流程重构、技术
- Spring AI 概述与功能简介
drebander
AI编程spring人工智能java
SpringAI是一个由Spring团队开发的开源框架,旨在为人工智能(AI)和机器学习(ML)提供一个成熟且高效的开发平台。它将Spring生态系统的设计理念应用于AI开发,尤其强调模块化、可移植性以及简洁的集成。SpringAI提供了丰富的功能,涵盖从AI模型的调用到与数据库的集成等多个方面,帮助开发者构建和管理AI驱动的应用程序。1.SpringAI背景SpringAI的背景源于Spring
- 在二分类任务中如何处理包含中文的类别特征
Dush32
分类数据挖掘人工智能机器学习数据分析
在机器学习中,处理类别特征(CategoricalFeatures)是常见的任务,特别是在中文数据中,很多类别特征如省份、城市等都是字符串类型。如何将这些类别变量转换为模型可以理解的数值格式,是每个数据科学家都必须面对的挑战。在这篇文章中,我们将探讨两种常见的类别特征编码方法:astype('category')和LabelEncoder,并比较它们在二分类任务中的效果。我们以“省份”这一类别特征
- 基于用户画像的商品推荐系统
Dush32
机器学习人工智能python推荐算法
随着人工智能和大数据技术的进步,产品推荐系统成为了现代广告与电商平台中不可或缺的部分。通过深度挖掘用户的行为数据,能够为广告主提供精准的用户画像,从而更高效地推荐相关产品,提升购买转化率。本项目基于科大讯飞AI营销云大赛的赛题,目的是利用用户画像进行产品推荐,预测用户是否会购买相应商品。我们使用了机器学习的二分类模型,通过分析用户的性别、年龄、常驻地、机型等信息,来判断用户的付费行为。项目目标:本
- AI原生应用领域多租户的技术架构剖析
AI天才研究院
AI-native架构人工智能ai
AI原生应用领域多租户技术架构深度剖析元数据框架标题:AI原生应用多租户技术架构:从隔离性到智能化的分层设计与实践关键词:AI原生应用、多租户架构、数据隔离、模型共享、云原生租户管理摘要:本文系统解析AI原生应用场景下多租户技术架构的核心设计逻辑,覆盖从数据层到模型层的全栈隔离与共享机制。通过第一性原理推导,结合云原生、机器学习生命周期管理(MLOps)等技术范式,提出包含租户上下文管理、动态资源
- Python爬虫实战:批量下载小红书笔记图片的全流程技术解析
Python爬虫项目
2025年爬虫实战项目python爬虫笔记开发语言音视频github
1.引言:为什么要爬取小红书笔记图片小红书作为新兴的生活方式分享平台,聚集了大量高质量原创笔记内容,涵盖时尚、美妆、旅游、美食等多领域。笔记中的图片往往是内容的核心,批量下载小红书笔记图片,有助于:内容归档与备份数据分析与用户行为研究图像识别与机器学习训练电商推广及内容再加工但小红书对内容保护做得较好,爬取难度较高,需要结合多技术手段突破。2.小红书平台特点与爬取难点动态加载与API接口多变:页面
- 【机器学习】必会降维算法之:独立成分分析(ICA)
Carl_奕然
机器学习算法人工智能
独立成分分析(ICA)1、引言2、独立成分分析(ICA)2.0引言2.1定义2.2应用场景2.3核心原理2.4实现方式2.5算法公式2.6代码示例3、总结1、引言小屌丝:鱼哥,最近胡塞武装很哇塞啊。小鱼:你什么时候开始关注军事了?小屌丝:这…还用关注吗?都上新闻了。小鱼:嗯,那你知道胡塞武装为什么这么厉害吗?小屌丝:额…当然是光脚不怕穿鞋的。小鱼:…你可真是…小屌丝:真是啥?小鱼:一个字,自己体会
- ica算法c语言,独立成分分析(ICA)的模拟实验(R语言)
weixin_39632212
ica算法c语言
本笔记是ESL14.7节图14.42的模拟过程。第一部分将以ProDenICA法为例试图介绍ICA的整个计算过程;第二部分将比较ProDenICA、FastICA以及KernelICA这种方法,试图重现图14.42。ICA的模拟过程生成数据首先我们得有一组独立(ICA的前提条件)分布的数据$S$(未知),然后经过矩阵$A_0$混合之后得到实际的观测值$X$,即$$X=SA_0$$也可以写成$$S=
- Java 大视界 -- Java 大数据机器学习模型在金融市场情绪分析与投资策略制定中的应用
青云交
大数据新视界Java大视界java大数据机器学习情绪分析智能投资多源数据
Java大视界--Java大数据机器学习模型在金融市场情绪分析与投资策略制定中的应用)引言:正文:一、金融情绪数据的立体化采集与治理1.1多模态数据采集架构1.2数据治理与特征工程二、Java机器学习模型的工程化实践2.1情感分析模型的深度优化2.2强化学习驱动的动态投资策略三、顶级机构实战:Java系统的金融炼金术四、技术前沿:Java与金融科技的未来融合4.1量子机器学习集成4.2联邦学习在合
- 安装python后如何安装numpy_如何简单安装NumPy与SciPy
2015-12-27回答numpy是一个定义了数值数组和矩阵类型和它们的基本运算的语言扩展。scipy是一种使用numpy来做高等数学、信号处理、优化、统计和许多其它科学任务的语言扩展。学习这两个工具的话,官方有很详细的文档和教程来帮助入门:我是传送门另外,还有一本书《numpyandscipy》,很薄,才67页:我是传送门如何安装numpy和scipy之所以写这篇文章主要是因为scipy官网貌似
- LeetCode[Math] - #66 Plus One
Cwind
javaLeetCode题解AlgorithmMath
原题链接:#66 Plus One
要求:
给定一个用数字数组表示的非负整数,如num1 = {1, 2, 3, 9}, num2 = {9, 9}等,给这个数加上1。
注意:
1. 数字的较高位存在数组的头上,即num1表示数字1239
2. 每一位(数组中的每个元素)的取值范围为0~9
难度:简单
分析:
题目比较简单,只须从数组
- JQuery中$.ajax()方法参数详解
AILIKES
JavaScriptjsonpjqueryAjaxjson
url: 要求为String类型的参数,(默认为当前页地址)发送请求的地址。
type: 要求为String类型的参数,请求方式(post或get)默认为get。注意其他http请求方法,例如put和 delete也可以使用,但仅部分浏览器支持。
timeout: 要求为Number类型的参数,设置请求超时时间(毫秒)。此设置将覆盖$.ajaxSetup()方法的全局
- JConsole & JVisualVM远程监视Webphere服务器JVM
Kai_Ge
JVisualVMJConsoleWebphere
JConsole是JDK里自带的一个工具,可以监测Java程序运行时所有对象的申请、释放等动作,将内存管理的所有信息进行统计、分析、可视化。我们可以根据这些信息判断程序是否有内存泄漏问题。
使用JConsole工具来分析WAS的JVM问题,需要进行相关的配置。
首先我们看WAS服务器端的配置.
1、登录was控制台https://10.4.119.18
- 自定义annotation
120153216
annotation
Java annotation 自定义注释@interface的用法 一、什么是注释
说起注释,得先提一提什么是元数据(metadata)。所谓元数据就是数据的数据。也就是说,元数据是描述数据的。就象数据表中的字段一样,每个字段描述了这个字段下的数据的含义。而J2SE5.0中提供的注释就是java源代码的元数据,也就是说注释是描述java源
- CentOS 5/6.X 使用 EPEL YUM源
2002wmj
centos
CentOS 6.X 安装使用EPEL YUM源1. 查看操作系统版本[root@node1 ~]# uname -a Linux node1.test.com 2.6.32-358.el6.x86_64 #1 SMP Fri Feb 22 00:31:26 UTC 2013 x86_64 x86_64 x86_64 GNU/Linux [root@node1 ~]#
- 在SQLSERVER中查找缺失和无用的索引SQL
357029540
SQL Server
--缺失的索引
SELECT avg_total_user_cost * avg_user_impact * ( user_scans + user_seeks ) AS PossibleImprovement ,
last_user_seek ,
- Spring3 MVC 笔记(二) —json+rest优化
7454103
Spring3 MVC
接上次的 spring mvc 注解的一些详细信息!
其实也是一些个人的学习笔记 呵呵!
- 替换“\”的时候报错Unexpected internal error near index 1 \ ^
adminjun
java“\替换”
发现还是有些东西没有刻子脑子里,,过段时间就没什么概念了,所以贴出来...以免再忘...
在拆分字符串时遇到通过 \ 来拆分,可是用所以想通过转义 \\ 来拆分的时候会报异常
public class Main {
/*
- POJ 1035 Spell checker(哈希表)
aijuans
暴力求解--哈希表
/*
题意:输入字典,然后输入单词,判断字典中是否出现过该单词,或者是否进行删除、添加、替换操作,如果是,则输出对应的字典中的单词
要求按照输入时候的排名输出
题解:建立两个哈希表。一个存储字典和输入字典中单词的排名,一个进行最后输出的判重
*/
#include <iostream>
//#define
using namespace std;
const int HASH =
- 通过原型实现javascript Array的去重、最大值和最小值
ayaoxinchao
JavaScriptarrayprototype
用原型函数(prototype)可以定义一些很方便的自定义函数,实现各种自定义功能。本次主要是实现了Array的去重、获取最大值和最小值。
实现代码如下:
<script type="text/javascript">
Array.prototype.unique = function() {
var a = {};
var le
- UIWebView实现https双向认证请求
bewithme
UIWebViewhttpsObjective-C
什么是HTTPS双向认证我已在先前的博文 ASIHTTPRequest实现https双向认证请求
中有讲述,不理解的读者可以先复习一下。本文是用UIWebView来实现对需要客户端证书验证的服务请求,网上有些文章中有涉及到此内容,但都只言片语,没有讲完全,更没有完整的代码,让人困扰不已。但是此知
- NoSQL数据库之Redis数据库管理(Redis高级应用之事务处理、持久化操作、pub_sub、虚拟内存)
bijian1013
redis数据库NoSQL
3.事务处理
Redis对事务的支持目前不比较简单。Redis只能保证一个client发起的事务中的命令可以连续的执行,而中间不会插入其他client的命令。当一个client在一个连接中发出multi命令时,这个连接会进入一个事务上下文,该连接后续的命令不会立即执行,而是先放到一个队列中,当执行exec命令时,redis会顺序的执行队列中
- 各数据库分页sql备忘
bingyingao
oraclesql分页
ORACLE
下面这个效率很低
SELECT * FROM ( SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_FS_RETURN order by id desc) A ) WHERE RN <20;
下面这个效率很高
SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_
- 【Scala七】Scala核心一:函数
bit1129
scala
1. 如果函数体只有一行代码,则可以不用写{},比如
def print(x: Int) = println(x)
一行上的多条语句用分号隔开,则只有第一句属于方法体,例如
def printWithValue(x: Int) : String= println(x); "ABC"
上面的代码报错,因为,printWithValue的方法
- 了解GHC的factorial编译过程
bookjovi
haskell
GHC相对其他主流语言的编译器或解释器还是比较复杂的,一部分原因是haskell本身的设计就不易于实现compiler,如lazy特性,static typed,类型推导等。
关于GHC的内部实现有篇文章说的挺好,这里,文中在RTS一节中详细说了haskell的concurrent实现,里面提到了green thread,如果熟悉Go语言的话就会发现,ghc的concurrent实现和Go有点类
- Java-Collections Framework学习与总结-LinkedHashMap
BrokenDreams
LinkedHashMap
前面总结了java.util.HashMap,了解了其内部由散列表实现,每个桶内是一个单向链表。那有没有双向链表的实现呢?双向链表的实现会具备什么特性呢?来看一下HashMap的一个子类——java.util.LinkedHashMap。
- 读《研磨设计模式》-代码笔记-抽象工厂模式-Abstract Factory
bylijinnan
abstract
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* Abstract Factory Pattern
* 抽象工厂模式的目的是:
* 通过在抽象工厂里面定义一组产品接口,方便地切换“产品簇”
* 这些接口是相关或者相依赖的
- 压暗面部高光
cherishLC
PS
方法一、压暗高光&重新着色
当皮肤很油又使用闪光灯时,很容易在面部形成高光区域。
下面讲一下我今天处理高光区域的心得:
皮肤可以分为纹理和色彩两个属性。其中纹理主要由亮度通道(Lab模式的L通道)决定,色彩则由a、b通道确定。
处理思路为在保持高光区域纹理的情况下,对高光区域着色。具体步骤为:降低高光区域的整体的亮度,再进行着色。
如果想简化步骤,可以只进行着色(参看下面的步骤1
- Java VisualVM监控远程JVM
crabdave
visualvm
Java VisualVM监控远程JVM
JDK1.6开始自带的VisualVM就是不错的监控工具.
这个工具就在JAVA_HOME\bin\目录下的jvisualvm.exe, 双击这个文件就能看到界面
通过JMX连接远程机器, 需要经过下面的配置:
1. 修改远程机器JDK配置文件 (我这里远程机器是linux).
- Saiku去掉登录模块
daizj
saiku登录olapBI
1、修改applicationContext-saiku-webapp.xml
<security:intercept-url pattern="/rest/**" access="IS_AUTHENTICATED_ANONYMOUSLY" />
<security:intercept-url pattern=&qu
- 浅析 Flex中的Focus
dsjt
htmlFlexFlash
关键字:focus、 setFocus、 IFocusManager、KeyboardEvent
焦点、设置焦点、获得焦点、键盘事件
一、无焦点的困扰——组件监听不到键盘事件
原因:只有获得焦点的组件(确切说是InteractiveObject)才能监听到键盘事件的目标阶段;键盘事件(flash.events.KeyboardEvent)参与冒泡阶段,所以焦点组件的父项(以及它爸
- Yii全局函数使用
dcj3sjt126com
yii
由于YII致力于完美的整合第三方库,它并没有定义任何全局函数。yii中的每一个应用都需要全类别和对象范围。例如,Yii::app()->user;Yii::app()->params['name'];等等。我们可以自行设定全局函数,使得代码看起来更加简洁易用。(原文地址)
我们可以保存在globals.php在protected目录下。然后,在入口脚本index.php的,我们包括在
- 设计模式之单例模式二(解决无序写入的问题)
come_for_dream
单例模式volatile乱序执行双重检验锁
在上篇文章中我们使用了双重检验锁的方式避免懒汉式单例模式下由于多线程造成的实例被多次创建的问题,但是因为由于JVM为了使得处理器内部的运算单元能充分利用,处理器可能会对输入代码进行乱序执行(Out Of Order Execute)优化,处理器会在计算之后将乱序执行的结果进行重组,保证该
- 程序员从初级到高级的蜕变
gcq511120594
框架工作PHPandroidhtml5
软件开发是一个奇怪的行业,市场远远供不应求。这是一个已经存在多年的问题,而且随着时间的流逝,愈演愈烈。
我们严重缺乏能够满足需求的人才。这个行业相当年轻。大多数软件项目是失败的。几乎所有的项目都会超出预算。我们解决问题的最佳指导方针可以归结为——“用一些通用方法去解决问题,当然这些方法常常不管用,于是,唯一能做的就是不断地尝试,逐个看看是否奏效”。
现在我们把淫浸代码时间超过3年的开发人员称为
- Reverse Linked List
hcx2013
list
Reverse a singly linked list.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
p
- Spring4.1新特性——数据库集成测试
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- C# Ajax上传图片同时生成微缩图(附Demo)
liyonghui160com
1.Ajax无刷新上传图片,详情请阅我的这篇文章。(jquery + c# ashx)
2.C#位图处理 System.Drawing。
3.最新demo支持IE7,IE8,Fir
- Java list三种遍历方法性能比较
pda158
java
从c/c++语言转向java开发,学习java语言list遍历的三种方法,顺便测试各种遍历方法的性能,测试方法为在ArrayList中插入1千万条记录,然后遍历ArrayList,发现了一个奇怪的现象,测试代码例如以下:
package com.hisense.tiger.list;
import java.util.ArrayList;
import java.util.Iterator;
- 300个涵盖IT各方面的免费资源(上)——商业与市场篇
shoothao
seo商业与市场IT资源免费资源
A.网站模板+logo+服务器主机+发票生成
HTML5 UP:响应式的HTML5和CSS3网站模板。
Bootswatch:免费的Bootstrap主题。
Templated:收集了845个免费的CSS和HTML5网站模板。
Wordpress.org|Wordpress.com:可免费创建你的新网站。
Strikingly:关注领域中免费无限的移动优
- localStorage、sessionStorage
uule
localStorage
W3School 例子
HTML5 提供了两种在客户端存储数据的新方法:
localStorage - 没有时间限制的数据存储
sessionStorage - 针对一个 session 的数据存储
之前,这些都是由 cookie 完成的。但是 cookie 不适合大量数据的存储,因为它们由每个对服务器的请求来传递,这使得 cookie 速度很慢而且效率也不
![]() ):
):![]() 为什么
为什么![]() 会是这个结果呢?我们来对照上文总结的两句话:标量不变,向量拉伸和f(x)横向拉,x纵向拉。对与这个例子,f(x)为标量,不需要变;x为向量,需要纵向拉伸,因此
会是这个结果呢?我们来对照上文总结的两句话:标量不变,向量拉伸和f(x)横向拉,x纵向拉。对与这个例子,f(x)为标量,不需要变;x为向量,需要纵向拉伸,因此![]() 就成为了nx1的矩阵。再根据矩阵求导本质:矩阵A中每个元素对矩阵B中每个元素求导。那么即f(x)对x1,x2,…xn分别求导。不知道讲到这里是否明白了些,还有疑惑的可以通过下面两个例子进行理解。
就成为了nx1的矩阵。再根据矩阵求导本质:矩阵A中每个元素对矩阵B中每个元素求导。那么即f(x)对x1,x2,…xn分别求导。不知道讲到这里是否明白了些,还有疑惑的可以通过下面两个例子进行理解。![]()
![]() 中f(x)为向量,所以要把每行都进行横拉伸,结果如下:
中f(x)为向量,所以要把每行都进行横拉伸,结果如下:![]()
![]() 是一个数(标量),化简后
是一个数(标量),化简后 ,这里也不在浪费篇幅证明,明白上述提示后,证明方法和①②* 基本一致。*
,这里也不在浪费篇幅证明,明白上述提示后,证明方法和①②* 基本一致。*![]() )注:对公式不明白的可以查找相关资料或自行推导。
)注:对公式不明白的可以查找相关资料或自行推导。