IIR数字滤波器的设计及应用——MATLAB
一、实验目的
(1)熟悉双线性变换法和双重映射法设计IIR数字滤波器的原理与方法。
(2)掌握IIR数字滤波器的MATLAB实现方法设计各种滤波器。
(3)观察分析滤波器输入输出数据波形,理解数字滤波的概念。
二、实验原理
1、IIR数字滤波器设计的一般方法
IIR数字滤波器设计最常采用的方式是先按技术指标设计模拟滤波器,然后采用合适的方法将模拟滤波器离散化为所需要的数字滤波器。按照这一方式,IR数字滤波器的设计过程为:
(1)确定数字滤波器实际需满足的技术指标参数;
(2)将数字滤波器设计的技术指标转换为模拟滤波器设计的技术指标;
(3)设计模拟滤波器,得到模拟滤波器的系统函数Ha(s);
(4)采用合适的离散化方法,将所设计的模拟滤波器离散化,为所需要的数字离散化,得到数字滤波器系统函数H(z)
2、常用模拟原型滤波器及其仿真计算方法
在设计数字滤波器之前所设计的模拟滤波器称为原型滤波器,常用的模拟原型滤波器有巴特沃斯模拟滤波器、切比雪夫模拟滤波器和椭圆模拟滤波器三种。Matlab环境中,三种模拟滤波器的仿真设计方法介绍如下:
(1)巴特沃斯模拟滤波器设计。MATIAB信号处理工具箱提供的用于巴特沃什模拟滤波器设计的函数主要是 buttord()和butter()。这两个函数的调用格式分别如下:
[N,wc]=buttord(wp,ws,Rp,Rs,'s')
Buttord()函数的调用用于计算巴特沃什模拟滤波器的阶次N和3dB截止频率。输入参数为四个,含义分别为:
Wp:通带截止频率;ws:阻带截止频率;Rp:通带最大衰减,单位为dB;Rs:阻带最小衰减,单位为dB。
函数调用后,可返回两个参数,分别是:
N:模拟滤波器的阶次;wc:模拟滤波器的3dB截止频率。在函数的使用中,当wp
[B,A]=butter(N, wc,'ftype','s’
Buttord()函数用于计算巴特沃什模拟滤波器系统函数中分子和分母多项式的系数向量B和A。输入参数为四个,含义分别为:
N:模拟滤波器的阶次;
wc:模拟滤波器的3dB截止频率;当设计的是低通或高通滤波器时,为一元向量;设计的是带通或带阻滤波器时,是二元向量,向量的两个元素分别为3dB上限截止频率和下限截止频率。
ftype:滤波器类型,缺省时默认设计低通(wc为一元向量)或带通(wc为二元向量)滤波器;ftype=high,设计高通滤波器,ftype=stop,设计带阻滤波器(wc为二元向量)。
s:固定,代表是模拟滤波器的设计。
函数调用后,可返回两个参数,分别是:
B:系统函数分子多项式系数向量;A:系统函数分母多项式系数向量。
由系数向量B和A可以写出模拟滤波器的系统函数为:

(2)切比雪夫模拟滤波器设计。MATIAB信号处理工具箱提供的用于第一类切比雪夫模拟滤波器设计的函数主要是 cheblord()和cheby1()。这两个函数的调用格式如
[N,wc]=cheblord(Wwp, ws,Rp,Rs,'s[B,A]=cheby1(N, we,'ftype','s')
这两个函数中的所有参数基本与前述的巴特沃什模拟滤波器设计函数调用中的参数含义一致,唯一的区别在于 wc指的是第一类切比雪夫模拟滤波器的通带截止频率,而不是3dB截止频率。
(3)椭圆模拟滤波器设计MATLAB信号处理工具箱提供的用于椭圆模拟滤波器设计的函数主要是ellipord()和 ellip()。这两个函数的调用格式和参数含义与前述几个函数基本类似,此处不再赘述。
3、模拟滤波器到数字滤波器的离散化方法
模拟滤波器设计完成后,由模拟滤波器到数字滤波器的离散化,有两种方式。即冲激响应不变法和双线性映射法。
冲激响应不变法即基本思想是:数字滤波器的单位取样响应是模拟滤波器单位冲激响应的采样值即:
h(n)= h(t)|t=nT
这种离散化方法能够保证数字角频率和模拟角频率之间严格的线性关系,从而不改变滤波器频率响应的形状,但会存在频率宁限滤波器的设计(低通和响应的混叠失真,因而只适合于进行带限滤波器的设计(低通和带通)。
双线性映射法主要为克服冲激响应不变法的混叠失真现象,其基本思想如下:
(1)先把模拟滤波器的s平面映射为s平面,即限制Ω在-Π/T~Π/T之间取值。
(2)然后采用冲激不变法的方式将s1平面映射到数字滤波器的z平面。
双线性映射法克服了混叠现象,但是模拟角频率和数字角频率之间不再满足严格的线性关系,故存在着频率响应的畸变为克服频率响应畸变的影响,在模拟滤波技术指标确定时需要进行反畸变校正,即:

MATLAB的数字信号处理工具箱提供impinvar()函数和
双线性映射法。这两个函bilinear 函数用以实现冲激响应不变法和数的调用格式如下:
[Bz,Az]= impinvar(B,A,fs)
[Bz,Az]= bilinear(B,A,fs)其中,B,A分别是H。(s)的分子、分母多项式的系数向量,Bz,Az分别是H(Z)的分子、分母多项式的系数向量,fs为采样频率。
4、IIR数字滤波器的实现方法
IIR数字滤波器的设计计算最终是获取滤波器的系统函数H(Z),但是应用所设计的数字滤波器对实际信号进行处理,一般是借助差分方程来实现的。即通过系统函数H(Z)获得滤波器系统的差分方程,然后根据差分方程利用顺序迭代的方式进行滤波器实现程序的编写。但需注意的是,顺序迭代程序之前需要赋初始条件,初始条件的个数取决于滤波器的阶次N。以二阶IIR数字滤波器为例,其实现程序如下:
(1)=x(1);
y(2)=(x(1)+x(2))/2;for n=3:length(x)
y(n)=b(1)*x(n)+b(2)*x(n-1)+b(3)*x(n-2)-a(2)*y(n-1)-a(3)*y(n-2);
end;
三、实验步骤、数据记录及处理
代码示例:
%输入并显示滤波前心电图采样序列;
clc;clear all;close all;%清空工作空间;
xn=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];%存入采样序列样本;
n=0:55;Fs=100;%设置时域序列与采样数频率;
figure('name','心电图时域与频域采样图')%定义绘图框标题名;
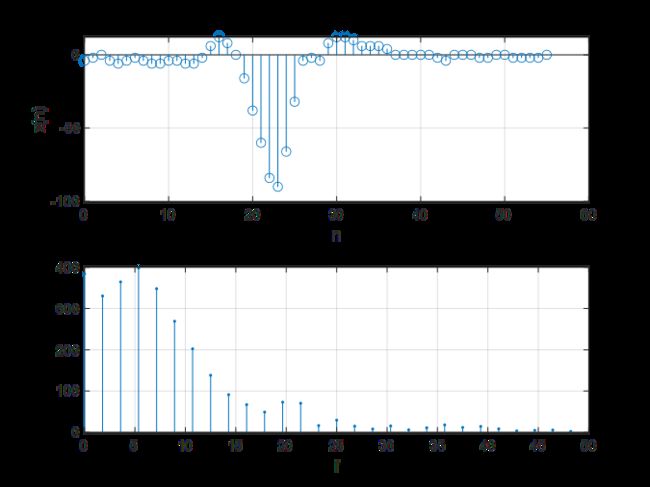
subplot(211);stem(n,xn);grid on;xlabel('n');ylabel('x(n)');title('心电图采样序列时域');%绘制时域采样图;
ndft=length(n);%采样数据点数;
Xk=fft(xn,ndft);%快速傅里叶变换;
mag=abs(Xk);%获得傅里叶变换后的振幅;
k=0:ndft/2-1;%离散时间序列;
f=Fs*k/ndft;%采样频率序列;
subplot(212);stem(f,mag(1:(ndft/2)),'.');grid on;xlabel('f');title('心电信号频谱图');%绘制采样频谱图;
clc;clear all;close all;%清空工作空间;
Fs=100;fp=15;fs=23;k1=-2;k2=-20;Ts=1/Fs;%定义信号采样频率;通带截止频率;通带起始频率;
wp=2*pi*fp;ws=2*pi*fs;%分别求出模拟通带截止频率wp和模拟阻带截止频率ws;
%wp=(2/Ts)*tan(wp/2);Ws=(2/Ts)*tan(ws/2);%分别求出数字通带截止频率Wp和数字阻带截止频率Ws;
[N,wc]=buttord(wp,ws,k1,k2,'s');%计算巴特沃什模拟滤波器的阶次;
N%显示巴特沃什模拟滤波器的阶次
[b1,a1]=butter(N,wc,'s');%计算H(s)系数向量b1和a1;
[H,m]=freqz(b1,a1);%计算巴特沃什模拟滤波器的频率响应;
mag=abs(H);%求巴特沃什模拟滤波器的幅频响应振幅;
pha=angle(H);%求巴特沃什模拟滤波器的相频响应相位;
db=20*log10((mag+eps)/max(mag));%将幅频特性转换为对数形式;
figure('name','巴特沃什模拟滤波器幅频相频特性')%定义巴特沃什模拟滤波器幅频相特性图形标题名
subplot(211);plot(m*100/(2*pi),db);grid on;xlabel('w/2pi');ylabel('db');title('巴特沃什模拟滤波器幅频特性');%绘制巴特沃什模拟滤波器幅频特性
subplot(212);plot(m*100/(2*pi),pha);grid on;xlabel('w/2pi');ylabel('rad');title('巴特沃什模拟滤波器相频特性');%巴特沃什模拟滤波器相频特性
clear all;clc;close all;%清空工作空间;
Fs=100;fp=15;fs=23;Rp=-2;Rs=-20;Ts=1/Fs;%定义信号采样频率;通带截止频率;通带起始频率;
wp=2*pi*fp;ws=2*pi*fs;%分别求出模拟通带截止频率wp和模拟阻带截止频率ws
[N,wc]=buttord(wp,ws,Rp,Rs,'s');%计算巴特沃什模拟滤波器的阶次
N%显示双线性数字滤波器的阶次
[b1,a1]=butter(N,wc,'s');%计算H(s)系数向量b1和a1
[b,a]=bilinear(b1,a1,Fs);%利用双线性映射法将巴特沃什模拟滤波器转换为数字滤波器
[H,m]=freqz(b,a);%计算巴特沃什数字滤波器的频率响应
mag=abs(H);%求巴特沃什数字滤波器的幅频响应
pha=angle(H);%求巴特沃什数字滤波器的相频响应
db=20*log10((mag+eps)/max(mag));%将幅频特性转换为对数形式
figure('name','双线性数字滤波器幅频相频特性')
subplot(211);plot(m*100/(2*pi),db);grid on;axis([0,56,-100,50]);xlabel('w/2pi');ylabel('db');title('双线性数字滤波器幅频特性');%绘制双线性数字滤波器幅频特性;
subplot(313);plot(m*100/(2*pi),pha);grid on;xlabel('w/2pi');ylabel('rad');title('双线性数字滤波器相频特性');%绘制双线性数字滤波器相频特性;
clear all;clc;close all;%清空工作空间;
%画出滤波前心电图采样序列
x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];
n=0:55;Fs=100;
figure('name','双线性映射法滤波后心电序列波形')
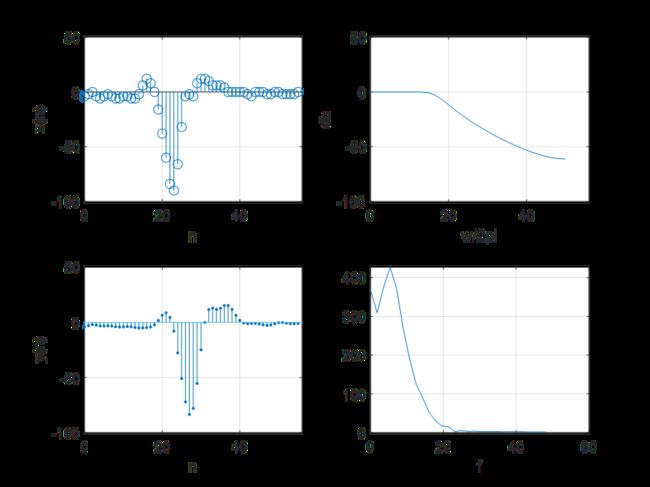
subplot(221);stem(n,x);grid on;axis([0,56,-100,50]);xlabel('n');ylabel('x(n)');title('滤波前心电图采样序列');
%画出双线性映射法将巴特沃什模拟滤波器转换为数字滤波器的幅频特性曲线
Fs=100;fp=15;fs=23;Rp=-2;Rs=-20;Ts=1/Fs;
wp=2*pi*fp;ws=2*pi*fs;%分别求出模拟通带截止频率wp和模拟阻带截止频率ws
[N,wc]=buttord(wp,ws,Rp,Rs,'s');%计算巴特沃什模拟滤波器的阶次
N%显示巴特沃什滤波器的阶次
[b1,a1]=butter(N,wc,'s');%计算H(s)系数向量b1和a1
[b,a]=bilinear(b1,a1,Fs);%利用双线性映射法将巴特沃什模拟滤波器转换为数字滤波器
[H,m]=freqz(b,a);%计算巴特沃什数字滤波器的频率响应
mag=abs(H);%求巴特沃什数字滤波器的幅频响应
db=20*log10((mag+eps)/max(mag));%将幅频特性转换为对数形式
subplot(222);plot(m*100/(2*pi),db);grid on;axis([0,56,-100,50]);xlabel('w/2pi');ylabel('db');title('双线性数字滤波器幅频特性');%绘制双线性数字滤波器幅频特性
%利用所设计出的滤波器差分方程
y(1)=x(1);
y(2)=(x(1)+x(2))/2;
y(3)=(x(1)+x(2)+x(3))/3;
y(4)=(x(1)+x(2)+x(3)+x(4))/4;
y(5)=(x(1)+x(2)+x(3)+x(4)+x(5))/5;
y(6)=(x(1)+x(2)+x(3)+x(4)+x(5)+x(6))/6;
for n=7:length(x);
y(n)=b(1)*x(n)+b(2)*x(n-1)+b(3)*x(n-2)+b(4)*x(n-3)+b(5)*x(n-4)+b(6)*x(n-5)+b(7)*x(n-6)-a(2)*y(n-1)-a(3)*y(n-2)-a(4)*y(n-3)-a(5)*y(n-4)-a(6)*y(n-5)-a(7)*y(n-6);
end
%绘制滤波后心电序列波形
subplot(223);
n=0:55;%设置时域序列
ndft=length(x);%采样数据点数;
stem(n,y,'.');grid on;axis([0,56,-100,50]);hold on;
n=0:60;%设置时域序列
m=zeros(61);
subplot(223);plot(n,m);grid on;xlabel('n');ylabel('y(n)');title('IIR数字滤波后心电采样序列');
Xk=fft(y,ndft);%快速傅里叶变换;
mag=abs(Xk);%获得傅里叶变换后的振幅;
k=0:ndft/2-1;%离散时间序列;
f=Fs*k/ndft;%采样频率序列;
subplot(224);plot(f,mag(1:(ndft/2)));grid on;xlabel('f');title('IIR数字滤波后心电信号频谱图');
clear all;clc;close all;%清空工作空间;
Fs=100;fp=15;fs=23;Rp=-2;Rs=-20;Ts=1/Fs;%定义信号采样频率;通带截止频率;通带起始频率;
wp=2*pi*fp;ws=2*pi*fs;%分别求出模拟通带截止频率wp和模拟阻带截止频率ws
[N,wc]=buttord(wp,ws,Rp,Rs,'s');%计算巴特沃什模拟滤波器的阶次
N%显示巴特沃什滤波器的阶次
[b1,a1]=butter(N,wc,'s');%计算H(s)系数向量b1和a1
[b,a]=impinvar(b1,a1,Fs);%利用冲激响应不变法将巴特沃什模拟滤波器转换为数字滤波器
[H,m]=freqz(b,a);%计算巴特沃什数字滤波器的频率响应
mag=abs(H);%求巴特沃什数字滤波器的幅频响应
pha=angle(H);%求巴特沃什数字滤波器的相频响应
db=20*log10((mag+eps)/max(mag));%将幅频特性转换为对数形式
figure('name','冲激响应不变法数字滤波器幅频相频特性')
subplot(211);plot(m*100/(2*pi),db);grid on;axis([0,56,-100,50]);xlabel('w/2pi');ylabel('db');title('冲激响应不变法数字滤波器幅频特性');
subplot(313);plot(m*100/(2*pi),pha);grid on;xlabel('w/2pi');ylabel('rad');title('冲激响应不变法数字滤波器相频特性');
clear all;clc;close all;
%画出滤波前心电图采样序列
x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];
n=0:55;Fs=100;
figure('name','冲激响应不变法滤波后心电序列波形')
subplot(221);stem(n,x);grid on;axis([0,56,-100,50]);xlabel('n');ylabel('x(n)');title('滤波前心电图采样序列');
%画出双线性映射法将巴特沃什模拟滤波器转换为数字滤波器的幅频特性曲线
Fs=100;fp=15;fs=23;Rp=-2;Rs=-20;Ts=1/Fs;
wp=2*pi*fp;ws=2*pi*fs;%分别求出模拟通带截止频率wp和模拟阻带截止频率ws
[N,wc]=buttord(wp,ws,Rp,Rs,'s');%计算巴特沃什模拟滤波器的阶次
N%显示巴特沃什滤波器的阶次
[b1,a1]=butter(N,wc,'s');%计算H(s)系数向量b1和a1
[b,a]=impinvar(b1,a1,Fs);%利用冲激响应不变法将巴特沃什模拟滤波器转换为数字滤波器
[H,m]=freqz(b,a);%计算巴特沃什数字滤波器的频率响应
mag=abs(H);%求巴特沃什数字滤波器的幅频响应
db=20*log10((mag+eps)/max(mag));%将幅频特性转换为对数形式
subplot(222);plot(m*100/(2*pi),db);grid on;axis([0,56,-100,50]);xlabel('w/2pi');ylabel('db');title('冲激响应不变数字滤波器幅频特性');
%利用所设计出的滤波器差分方程
y(1)=x(1);
y(2)=(x(1)+x(2))/2;
y(3)=(x(1)+x(2)+x(3))/3;
y(4)=(x(1)+x(2)+x(3)+x(4))/4;
y(5)=(x(1)+x(2)+x(3)+x(4)+x(5))/5;
y(6)=(x(1)+x(2)+x(3)+x(4)+x(5)+x(6))/6;
for n=7:length(x);
y(n)=b(1)*x(n)+b(2)*x(n-1)+b(3)*x(n-2)+b(4)*x(n-3)+b(5)*x(n-4)+b(6)*x(n-5)+b(7)*x(n-6)-a(2)*y(n-1)-a(3)*y(n-2)-a(4)*y(n-3)-a(5)*y(n-4)-a(6)*y(n-5)-a(7)*y(n-6);
end
%绘制滤波后心电序列波形
subplot(223);
n=0:55;
ndft=length(x);
stem(n,y,'.');grid on;axis([0,56,-100,50]);
hold on;
n=0:60;
m=zeros(61);
subplot(223);plot(n,m);grid on;
xlabel('n');ylabel('y(n)');title('IIR数字滤波后心电采样序列');
Xk=fft(y,ndft);
mag=abs(Xk);
k=0:ndft/2-1;
f=Fs*k/ndft;
subplot(224);
plot(f,mag(1:(ndft/2)));grid on;
xlabel('f');title('IIR数字滤波后心电信号频谱图');
四、分析
分析略
五、思考题
思考题略
六、总结
总结略