C语言数据结构、十字链表的分析及实现

目录

前言

一、什么是十字链表

二、认识十字链表

1.十字链表的组成

2.顶点和弧的连接

三、代码逻辑实现

1.出度

 2.入度

总结

---

---

前言

  无论是什么程序都要和数据打交道，一个好的程序员会选择更优的数据结构来更好的解决问题，因此数据结构的重要性不言而喻。数据结构的学习本质上是让我们能见到很多前辈在解决一些要求时间和空间的难点问题上设计出的一系列解决方法，我们可以在今后借鉴这些方法，也可以根据这些方法在遇到具体的新问题时提出自己的解决方法。（所以各种定义等字眼就不用过度深究啦，每个人的表达方式不一样而已），在此以下的所有代码都是仅供参考，并不是唯一的答案，只要逻辑上能行的通，写出来的代码能达到相同的结果，并且在复杂度上差不多，就行了。

---

一、什么是十字链表

在上篇文章的最后，我们分析了邻接表的优劣，邻接表本身并没有什么大的缺陷，如果说有缺点，那么是对于有向图而言对同时表示一个顶点的出度和入度麻烦，因为需要有邻接表和逆邻接表同时表示，而且这种应用场景是存在的。十字链表就是为了使这个问题得到解决而出现的。

所以十字链表就是一种将邻接表和逆邻接表结合在一起的一种图的存储结构，它针对的就是有向图中出度和入度一起使用的情况，并且大大节省了内存。

二、认识十字链表

1.十字链表的组成

十字链表是由数组+链表的形式构成的，数组用来记录顶点的信息，链表用来记录弧（边）的信息。

在有向图中，顶点集的存储结构如下图所示

其中data是数据域，用于记录顶点的信息，而firstIn和firstOut是两个指针，指向的是以该节点为弧头（In）或弧尾（Out）的第一节点。

 对于如此一个有向图而言，弧头和弧尾的概念是人为设置的，在这里我们假定一个顶点的入度指向弧头，出度的方向为弧尾

 它的顶点数组应该这么表示，为了方便讲解，这里我们假定输入的值就是对应的下标，实际上应该通过用户输入的值在顶点数组中找到对应的下标

代码实现

//顶点集
typedef struct VexNode
{
    //数据域
    int data;
    ArcBox* firstIn, *firstOut;//以该节点为弧头或弧尾的首节点
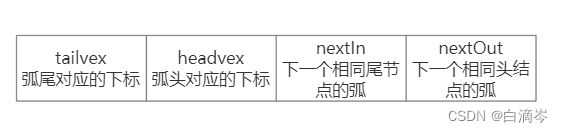
}VexNode;

 在有向图中每一个顶点与之对应的弧，具体的弧的存储结构如下所示

其中tailvex表示的是在这一条弧中弧尾节点在顶点数组中对应的下标，headvex表示的是在这一条弧中弧头节点在顶点数组中对应的下标；（实际上应该还有一个代表权值的元素weight，但这里不做描述）

代码实现

//边集(弧集)
typedef struct ArcBox
{
    int tailvex, headvex;//弧尾 弧头对应的顶点下标
    struct AcrBox* nextIn, *nextOut;//下一个相同尾节点的弧 下一个相同头节点的弧
}ArcBox;

然而在代码逻辑上，我们还是需要一个抽象结构，也就是可以用一个结构体把顶点集合与弧的集合联系在一起，构建十字链表

#define MAXVEX 200
typedef struct X
{
    //存储顶点的一维数组
    VexNode* Xlist[MAXVEX];
    int numV, numA;//顶点数 弧数
}OLGraph;

2.顶点和弧的连接

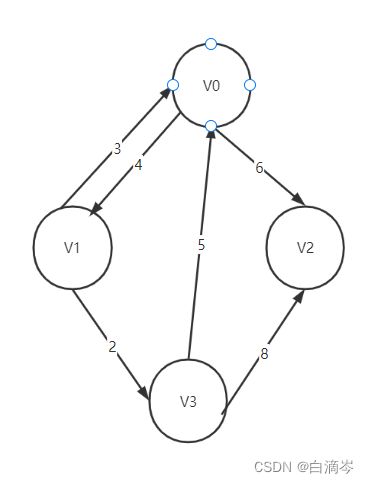
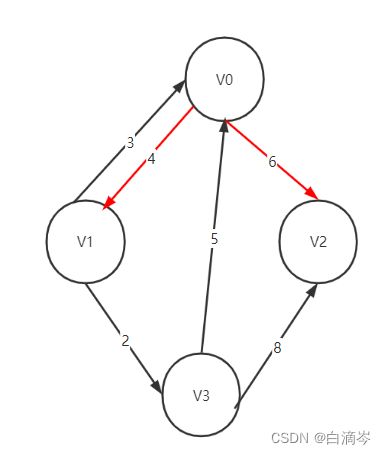
还是对于这样一个有向图，我们以节点V0为例，可以看到与V0有关的弧有四条，分别是：（V0，V1）、（V0，V2）、（V1，V0）、（V3，V0）因为这是一个有向图，所以我们应该以有向图的入度和出度的形式去观察V0节点，很明显（V0，V1）、（V0，V2）两条弧表示V0的出度，而（V1，V0）、（V3，V0）表示的是V0的入度

结合上文的描述，我们可以构建出这个有向图的顶点集合与弧集，我把它们具现化为如下图表

怎么理解这张图表呢？左边的图表表示的是从V0到V3的顶点的集合，data是V0到V3的值；右边的离散的表格代表的就是有向图中一条一条的弧，也就是每个顶点对应的弧的集合

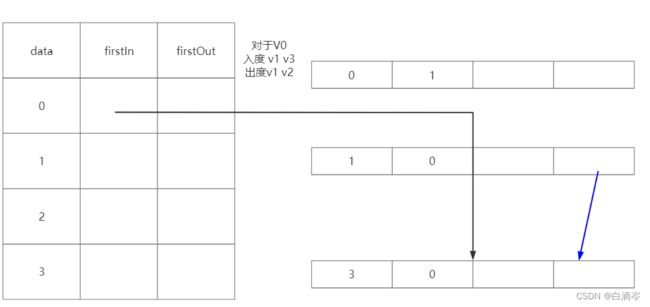
我还是以V0为例，对于V0入度节点是V1和V3，出度节点是V1和V2，现在要根据上文的描述，把V0的顶点集合和与V0有关的弧的集合联系起来

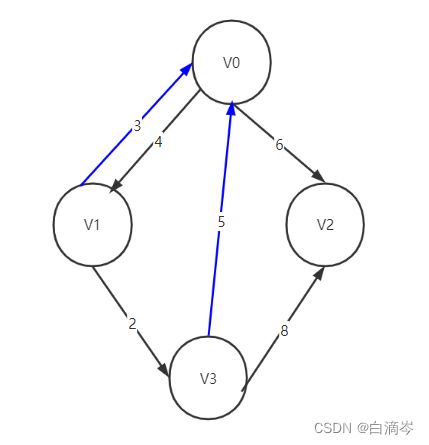
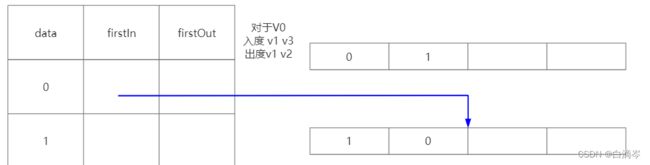
 对于顶点集合的结构来说，firstOut应该指向V0的第一个出度节点，从逻辑上来说没有先后排序，但从代码上的步骤是遍历V0的所有的邻接点去判断，所以这里firstOut应该指向弧（V0，V1），如下图所示

 

 而在弧集中的结构来说，nextIn表示的是指向下一个相同尾节点的弧，对于弧（V0，V1）和弧（V0，V2）它们都是从V0开始，也就是它们有着同一个尾节点V0，所以弧（V0，V1）的nextIn应该指向的是弧（V0，V2）

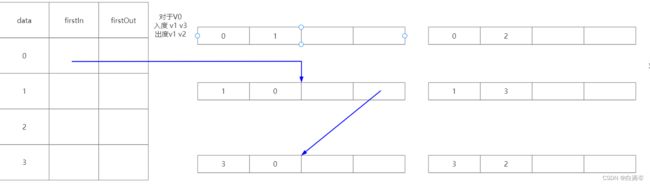
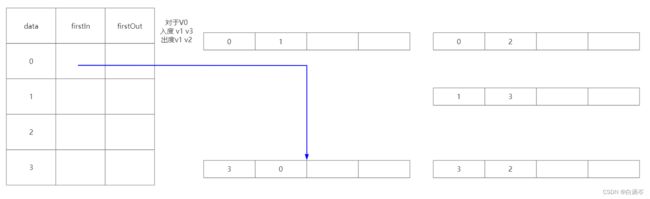
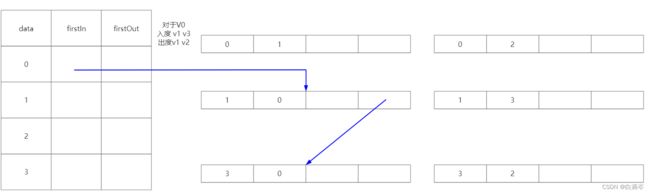
对于顶点集合的结构来说，firstIn应该指向V0的第一个入度节点，从逻辑上来说没有先后排序，但从代码上的步骤是遍历V0的所有的邻接点去判断，所以这里firstIn应该指向弧（V1，V0），如下图所示

 

  而在弧集中的结构来说，nextOut表示的是指向下一个相同头节点的弧，也就是弧头所指向的都是V0的弧，即弧（V1，V0）的nextOut应该指向弧（V3，V0）

这个时候与顶点V0和其有关所有的弧都联系上了。其它的节点同理

三、代码逻辑实现

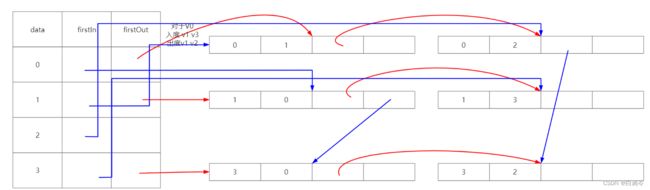
在代码逻辑上对上文描述的顶点和弧的连接采用了链表中的头插法，逻辑比较简单，不清楚的可以在纸上画一画就清楚了

（黑线代表原来的连接，红线或蓝色代表头插以后的连接）

1.出度

①

②

 ③

 2.入度

①

②

③

代码实现

void creatDG(OLGraph* G)
{
    int vi, vj;
    //输入有向图的顶点数和边数
    scanf_s("%d%d", &G->numV, &G->numA);
    //输入顶点集的数据
    for(int i = 0; i < G->numV; i++)
    {
        scanf_s("%d", &G->Xlist[i]->data);
        G->Xlist[i]->firstIn = NULL;
        G->Xlist[i]->firstOut = NULL;
    }
    //构建十字链表
    for(int i = 0; i < G->numA; i++)
    {
        //输入值 查找相对应的下标
        //这里就当直接输入下标
        scanf_s("%d%d", &vi, &vj);
        //建立弧的节点
        ArcBox* p = (ArcBox*)malloc(sizeof(ArcBox));
        p->tailvex = vi;
        p->tailvex = vj;
        //头插法插入新的边表节点p
        p->nextIn = G->Xlist[vj]->firstIn;//指向弧头相同的下一个弧
        p->nextOut = G->Xlist[vi]->firstOut;//指向弧尾相同的下一个弧
        G->Xlist[vi]->firstOut = G->Xlist[vj]->firstIn = p; 
    }
}

总结

 全部代码

#include
#include
#define MAXVEX 200
//十字链表
//边集(弧集)
typedef struct ArcBox
{
    int tailvex, headvex;//弧尾 弧头对应的顶点下标
    struct AcrBox* nextIn, *nextOut;//下一个相同尾节点的弧 下一个相同头节点的弧
}ArcBox;
//顶点集
typedef struct VexNode
{
    //数据域
    int data;
    ArcBox* firstIn, *firstOut;//以该节点为弧头或弧尾的首节点
}VexNode;
//构建十字链表
typedef struct X
{
    //存储顶点的一维数组
    VexNode* Xlist[MAXVEX];
    int numV, numA;//顶点数 弧数
}OLGraph;

void creatDG(OLGraph* G)
{
    int vi, vj;
    //输入有向图的顶点数和边数
    scanf_s("%d%d", &G->numV, &G->numA);
    //输入顶点集的数据
    for(int i = 0; i < G->numV; i++)
    {
        scanf_s("%d", &G->Xlist[i]->data);
        G->Xlist[i]->firstIn = NULL;
        G->Xlist[i]->firstOut = NULL;
    }
    //构建十字链表
    for(int i = 0; i < G->numA; i++)
    {
        //输入值 查找相对应的下标
        //这里就当直接输入下标
        scanf_s("%d%d", &vi, &vj);
        //建立弧的节点
        ArcBox* p = (ArcBox*)malloc(sizeof(ArcBox));
        p->tailvex = vi;
        p->tailvex = vj;
        //头插法插入新的边表节点p
        p->nextIn = G->Xlist[vj]->firstIn;//指向弧头相同的下一个弧
        p->nextOut = G->Xlist[vi]->firstOut;//指向弧尾相同的下一个弧
        G->Xlist[vi]->firstOut = G->Xlist[vj]->firstIn = p; 
    }
}

如果在一个项目中，需要频繁的对一个图的边（弧）增删改查呢？那么对十字链表来说增加或删除一条边有可能就会牵一发而动全身呢？是不是操作很麻烦？这就是十字链表的缺点，那么又存在什么样的结构可以解决上述问题呢？我们下一篇文章再解析。