邻接矩阵和邻接表

图的概述和存储结构（一）

---

---

前言

有一种说法是程序是由数据结构和算法组成的，这很能体现出数据结构在编码中的重要性。而代码优化的能力也是区别有基础的程序员和码农的重要标准，所以对于这一块的学习一定要稳重与细致，每一个章节都要实打实敲出能够实现该种结构的代码才算完成。

数据结构的学习本质上是让我们能见到很多前辈在解决一些要求时间和空间的难点问题上设计出的一系列解决方法，我们可以在今后借鉴这些方法，也可以根据这些方法在遇到具体的新问题时提出自己的解决方法。（所以各种定义等字眼就不用过度深究啦，每个人的表达方式不一样而已）在此以下的所有代码都是仅供参考，绝对不是唯一的答案，任何一种操作能达到相同的结果，只要逻辑上能行的通，复杂度上差不多，是无所谓怎么去实现最后的功能的。

---

一、图的概述

图是由两个集合组成的V代表顶点集合 E代表边集合（一个顶点偶数对）

1）图的分类

1.简单图
在图当中如果不存在顶点到其自身的边 且边不重复 的图叫做简单图；

2.无向图与有向图
没有方向的图是无向图、每条边都有方向的是有向图；

3.完全图
如果图中任意两个节点之间都存在一条边 称之为完全图。

2）图的要素

1.端点和邻接点
在无向图中存在（i，j）那么顶点i和顶点j是两个端点 且 i和j互为邻接点；
在有向图中（i，j）那么顶点i是起点，顶点 j是终点；

2.度
无向图中顶点具有的边的数目就是度
有向图中
入度 以该顶点进入边的数目,
出度 以该顶点出去边的数目;

3.子图
有一个图是另一个图的顶点的子集,并且边的关系一致;

4.路径 路径长度
对于这个图

ADE是一条路径 很明显路径不止一条
而路径长度，是A到D到E边的数目

5.连通 连通图 连通分量
如果两个节点之间有路径 那么就是连通的如果任意节点连通 那么就是连通图
一个无向图中 一个极大连通子图（再多一个节点就连通不上了） 就是连通分量
一个有向图中 一个极大连通子图（再多一个节点就连通不上了） 就是强连通分量

6.稠密图 和 稀疏图
通常认为n个节点的图边数为nlogn那么小于nlogn的边叫稀疏图大于的叫稠密图
事实上视具体情况而定

7.权 和 网
图中每一条边所对应的数字 就叫权值（可以理解为对于工期 需要的时间）
对于带权的图 就称网

8.连通图的生成树
就是一个极小连通图（再减去一条边就不连通了）
生成树不止一个

二、图的存储结构

图的存储分为：邻接矩阵 邻接表 十字链表 邻接多重表 边集数组

三、邻接矩阵

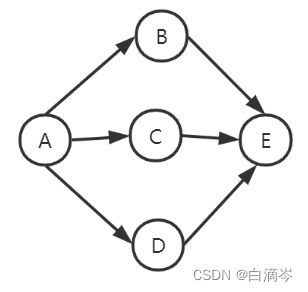
对于如此一个无向图而言 我们应该考虑怎么样去实现存储图的顶点和边的信息，

实际上我们可以用一个一维数组存储顶点的信息 和 二维数组来边的信息

这是一个二维数组的具现化表格，表头代表的是顶点的下标

对一个非带权的图 0代表没有边 1代表有边，值得注意的是在实际中顶点指向自己的边是没有意义的，即对角线恒为0

如果是带权的图 初始化为0或者为一个不可能的值（如65535

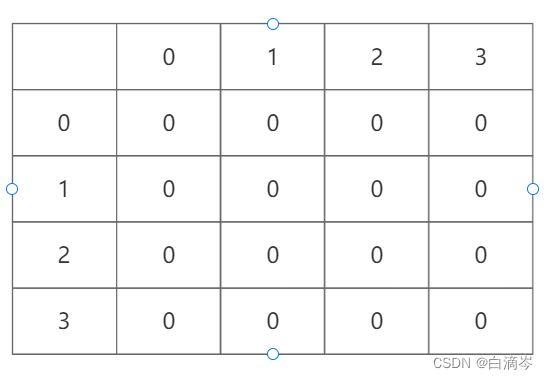
那么对如此一个无向图，可以得到以下表格

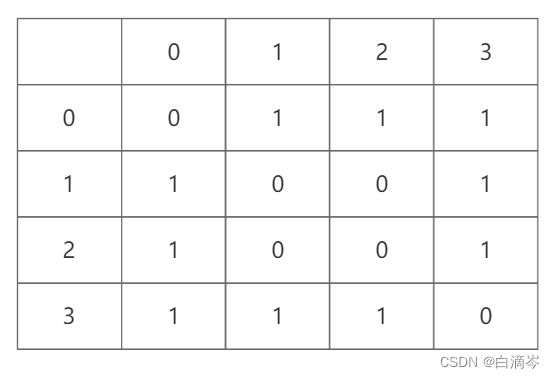
因为是无向图，顶点i既连接顶点j，又被顶点j连接，所以无向图是对称的关系

那么我们只要把上表的数据写入二维数组就是邻接矩阵

#include 
#include 
#define MaxVertices 100
//邻接矩阵
typedef struct AdjacentMatrix
{
    //顶点集
    int Vertices[MaxVertices];
    //边集
    int Edge[MaxVertices][MaxVertices];
    //顶点数 边数
    int numV, numE;
}AdjMatrix;

void creategrahp(AdjMatrix* G)
{
    int n, e;//n代表顶点数 e代表边数
    int vi, vj;//vi vj代表边的两个顶点对
    printf("要输入的顶点数和边数\n");
    scanf_s("%d%d",&n,&e);
    G->numV = n; 
    G->numE = e;
    //图的初始化
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            if(i == j)
            {
                //一个非带权的图 0代表没有边 1代表有边
                //边不指向自己 即对角线为0
                G->Edge[i][j] = 0;
            }
            else
            {
                //如果是带权的图 初始化为0或者为一个不可能的值
                G->Edge[i][j] = 65535;
            }
        }
    }
    //将顶点存入数组
    for(int i = 0; i < G->numV; i++)
    {
        printf("请输入第%d个节点的信息\n",i + 1);
        scanf_s("%d", &G->Vertices[i]);
    }
    //输入边的信息
    for(int i = 0; i< G->numE; i++)
    {
        //如果输入的是顶点的值 需要从顶点集中查找对应的下标 
        //如果是带权图 还要输入权的信息
        printf("请输入边的信息Vi,Vj\n");
        scanf_s("%d%d",&vi,&vj);
        G->Edge[vi][vj] = 1;
        //如果是带权图 等于权值
        //如果是有向图 就不对称
        //如果是无向图 矩阵对称
        G->Edge[vj][vi] = 1;
    }
}

四、邻接表

对于邻接矩阵来说如果图的边比较少，那么是空间浪费的，而邻接表弥补了这个缺点

邻接表
数组（顶点集）+链表（边集）的形式

顶点集

#define MAXVEX 100//表示顶点的数目
typedef struct VertexNode
{
    //存放信息的值
    char data;
    //边表的头指针
    EdgeNode* first;
}VertexNode;

边集

//边表的结构
typedef struct EdgeNode
{
    //邻接的点所对应的下标
    int adjvex;
    //指向下一个的指针
    struct EdgeNode* Next;
    //权值
    int weight;
}EdgeNode;

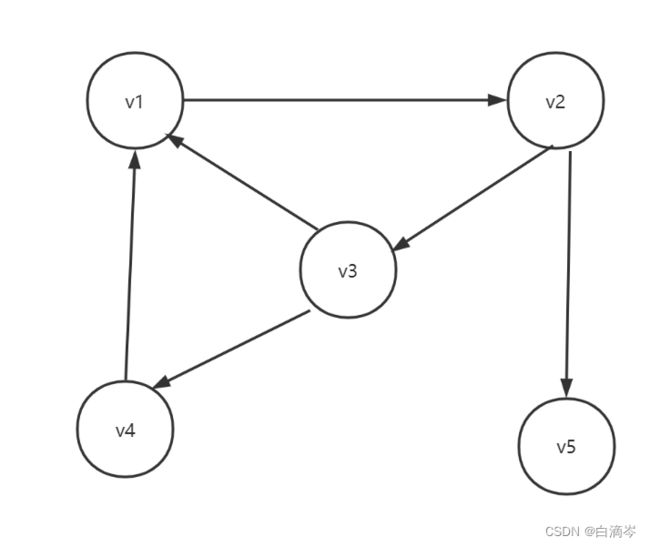
还是对这么一个无向图而言

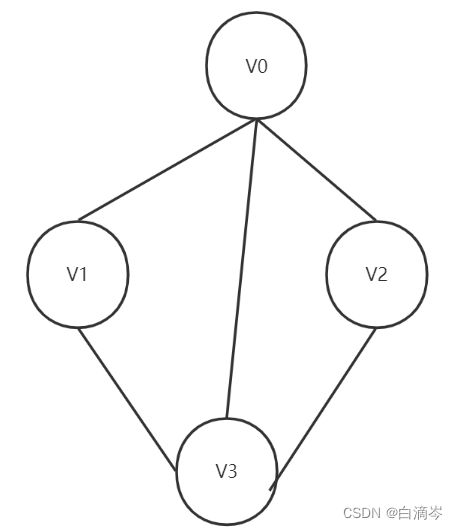
由上述的数组（顶点集）+链表（边集）我们可以画出以下关系图

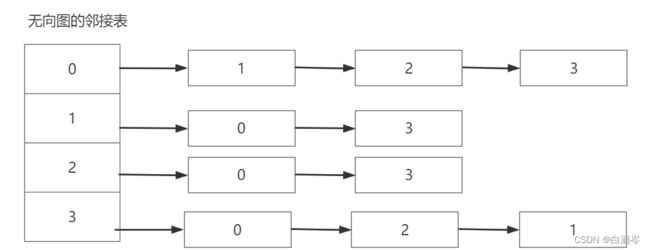
我把第一排单独拿出细说。
从无向图中我们可以看出节点V0与 V1 V2 V3三个节点连通，那么对于V0的顶点集来说，记录的是V0的数据和从V0出发指向其邻接点的指针（因为是无向图所以指针firstarc指向的第一个邻接点 可以是无先后顺序的）；

V0的边集应该记录的这个邻接的点所对应的下标、指向下一个邻接点的指针、和权值（这里没有）

那么很容易能得到这张关系图，而其他的节点是一样的

#include
#include
//邻接表
#define MAXVEX 100//表示顶点的数目
//边表的结构
typedef struct EdgeNode
{
    //邻接的点所对应的下标
    int adjvex;
    //指向下一个的指针
    struct EdgeNode* Next;
    //权值
    int weight;
}EdgeNode;
//顶点表的结构
typedef struct VertexNode
{
    //存放信息的值
    char data;
    //边表的头指针
    EdgeNode* first;
}VertexNode;
//邻接表的抽象结构
typedef struct
{
    //顶点集合数组
    VertexNode adjlist[MAXVEX];
    //顶点的数量 边的数量
    int numV, numE;
}Adjlist;

//以无向图构建邻接表
void creatadjlist(Adjlist* G)
{
    printf("输入顶点数和边数\n");
    scanf("%d%d", &G->numV, G->numE);
    //输入顶点信息
    for(int i = 0; i < G->numV; i++)
    {
        scanf("%c", &G->adjlist[i]);
        getchar();//清空缓存区
        G->adjlist[i].first = NULL;
    }
    //输入边的信息
    //接收边的顶点偶数对的信息
    int vi, vj;
    for(int i = 0; i < G->numE; i++)
    {
        scanf("%d%d", &vi, &vj);
        getchar();
        EdgeNode* e1 = (EdgeNode*)malloc(sizeof(EdgeNode));
        //判断是否创建成功
        if(e1 == NULL)
        {
            printf("MALLOC FAIL\n");
            exit(-1);
        }
        else
        {
            //头插
            //这里的下标 就用vi vj表示
            e1->adjvex = vj;
            e1->Next = G->adjlist[vi].first;
            G->adjlist[vi].first = e1;
            //如果是无向图 反向插入一遍
            EdgeNode* e2 = (EdgeNode*)malloc(sizeof(EdgeNode));
            e2->adjvex = vi;
            e2->Next = G->adjlist[vj].first;
            G->adjlist[vj].first = e2;
        }
    }
}

而对于一个有向图而言，有向图的邻接表代表出度，逆邻接表表达入度

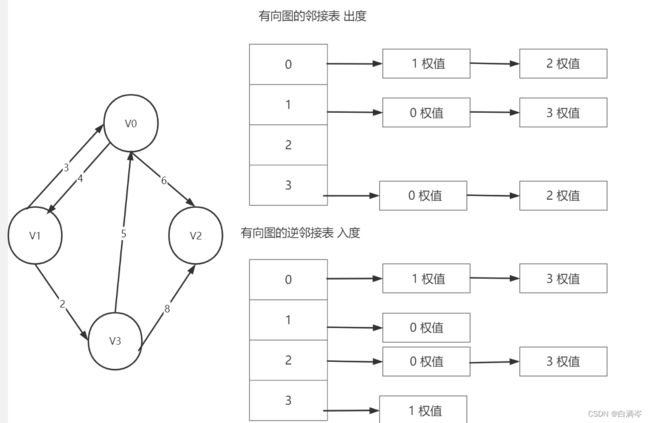
对于带权图一个元素代表出度顶点的下标，另一个元素代表边的权值

二者在代码上与无向图的邻接表没什么大的区别

邻接表可以说解决了邻接矩阵空间浪费的问题，并且邻接表本身并没有什么大的缺陷，如果说有缺点，那么是对于有向图而言对同时表示一个顶点的出度和入度麻烦，因为需要有邻接表和逆邻接表同时表示，那么有没有一种结构能解决这个问题呢？且听下回分解

还是那句话代码仅供参考，不是唯一答案