常用激活函数activation function（Softmax、Sigmoid、Tanh、ReLU和Leaky ReLU) 附激活函数图像绘制python代码

激活函数是确定神经网络输出的数学方程式。

激活函数的作用：给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数。

1、附加到网络中的每个神经元，并根据每个神经元的输入来确定是否应激活。

2、有助于将每个神经元的输出标准化到1到0或-1到1的范围内。

常用非线性激活函数对比

激活函数

公式

函数图像

适合场景

Softmax

多分类任务输出层

Sigmoid

二分类任务输出层，模型隐藏层

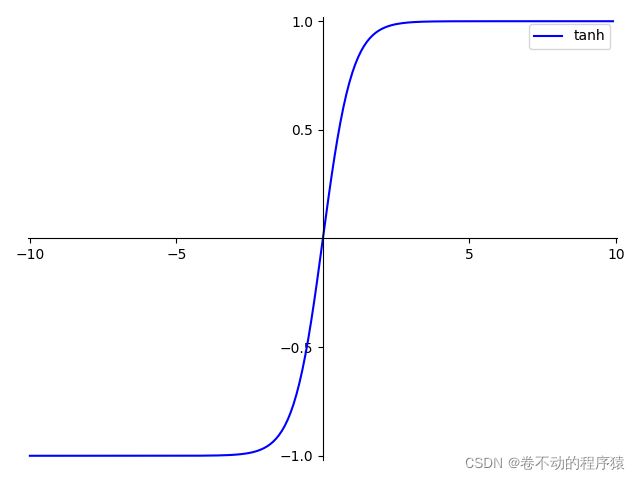
Tanh

ReLU

回归任务，卷积神经网络隐藏层

Leaky ReLU

激活函数必须满足：

• 可微，优化方法是基于梯度。
• 单调，保证单层网络是凸函数。
• 输出值范围，有限则梯度优化更稳定，无限则训练更高效（学习率需要更小）。

1、Softmax（也可视作激活函数）

常用且重要的一种归一化函数，其将输入值映射为0-1之间的概率实数，常用于多分类。

公式：

2、Sigmoid

使用范围最广的一种激活函数，具有指数形状。

公式：

优点：

在物理意义上最为接近神经元，输出是（0，1），可以被表示做概率或者用于输入的归一化，平滑的渐变，防止输出值“跳跃”。

缺点：

饱和性，从图中也不难看出其两侧导数逐渐趋近于0，可能导致梯度消失问题。

偏移现象，输出值均大于0，使得输出不是0的均值，这会导致后一层的神经元将得到上一层非0均值的信号作为输入。

梯度消失：导数值变得接近于0，导致反向传播的梯度也变得非常小，此时网络参数可能不更新。

3、Tanh（双曲正切）

公式：

优点：输出均值为0，使其收敛速度比较快，减少了迭代更新的次数。

缺点：饱和性，容易导致梯度消失。

4、ReLU（Rectified Linear Units）

公式：

优点：缓解sigmoid和tanh的饱和性，当x大于0时不存在饱和性问题，计算效率高，允许网络快速收敛。

缺点：神经元死亡和偏移现象影响网络收敛性**。**

神经元死亡：随着训练，部分输入会落入硬饱和区（小于0的区域），导致权重无法更新。

5、Leaky ReLU

公式：

优点：通过在小于0部分添加参数α，解决硬饱和问题。

缺点：不稳定，结果不一致，无法为正负输入值提供一致的关系预测（不同区间函数不同）。

图像绘制代码（Python）：

import math
from matplotlib import pyplot as plt
import numpy as np

def softmax(x):
    return np.exp(x)/np.sum(np.exp(x), axis=0)

def sigmoid(x):
    return 1. / (1 + np.exp(-x))

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

def relu(x):
    return np.where(x < 0, 0, x)

def prelu(x):
    return np.where(x < 0, 0.1 * x, x)

'''
def sigmoid(x):
    result = 1 / (1 + math.e ** (-x))
    return result
'''
def plot_softmax():
    x = np.linspace(-10, 10, 200)
    y = softmax(x)
    plt.plot(x, y, label="softmax", linestyle='-', color='blue')
    plt.legend()
    plt.savefig("softmax.png")
    #plt.show()

def plot_sigmoid():
    fig = plt.figure()
    ax = fig.add_subplot(111)
    x = np.linspace(-10, 10)
    y = sigmoid(x)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.set_xticks([-10, -5, 0, 5, 10])
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))
    ax.set_yticks([-1, -0.5, 0.5, 1])
    plt.plot(x, y, label="Sigmoid", linestyle='-', color='blue')
    plt.legend()
    plt.savefig("sigmoid.png")
    #plt.show()

def plot_tanh():
    x = np.arange(-10, 10, 0.1)
    y = tanh(x)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.spines['left'].set_position(('data', 0))
    ax.spines['bottom'].set_position(('data', 0))
    ax.plot(x, y, label="tanh", linestyle='-', color='blue')
    plt.legend()
    plt.xlim([-10.05, 10.05])
    plt.ylim([-1.02, 1.02])
    ax.set_yticks([-1.0, -0.5, 0.5, 1.0])
    ax.set_xticks([-10, -5, 5, 10])
    plt.tight_layout()
    plt.savefig("tanh.png")
    #plt.show()

def plot_relu():
    x = np.arange(-10, 10, 0.1)
    y = relu(x)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.spines['left'].set_position(('data', 0))
    ax.plot(x, y, label="relu", linestyle='-', color='blue')
    plt.legend()
    plt.xlim([-10.05, 10.05])
    plt.ylim([0, 10.02])
    ax.set_yticks([2, 4, 6, 8, 10])
    plt.tight_layout()
    plt.savefig("relu.png")
    #plt.show()

def plot_prelu():
    x = np.arange(-10, 10, 0.1)
    y = prelu(x)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.spines['left'].set_position(('data', 0))
    ax.spines['bottom'].set_position(('data', 0))
    ax.plot(x, y, label="leaky-relu", linestyle='-', color='blue')
    plt.legend()
    plt.xticks([])
    plt.yticks([])
    plt.tight_layout()
    plt.savefig("leaky-relu.png")
    #plt.show()

if __name__ == "__main__":
    plot_softmax()
    plot_sigmoid()
    plot_tanh()
    plot_relu()
    plot_prelu()