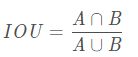NMS及IOU原理讲解和代码解析
NMS
NMS(non maximum suppression),中文名非极大值抑制,在很多计算机视觉任务中都有广泛应用,如:边缘检测、目标检测等。这里主要以人脸检测中的应用为例,来说明NMS。
以下图为例,由于滑动窗口,同一个人可能有好几个框(每一个框都带有一个分类器得分)。而我们的目标是一个人只保留一个最优的框:于是我们就要用到非极大值抑制,来抑制那些冗余的框: 抑制的过程是一个迭代-遍历-消除的过程。主要分为以下三步:
(1)将所有框的得分排序,选中最高分及其对应的框:
![]()
(2)遍历其余所有的框,如果和当前最高分框的重叠面积(IOU)大于一定阈值,我们就将框删除。
![]()
(3)从未处理的框中继续选一个得分最高的,重复上述过程。
![]()
原理还是很简单的,接下来看一下具体的代码示例:
import numpy as np
def nms(arry, thresh):
x1 = arry[:, 0]
y1 = arry[:, 1]
x2 = arry[:, 2]
y2 = arry[:, 3]
con = arry[:, 4]
# 获取四个目标框的面积
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
order = con.argsort()[::-1]
res = []
# 进行遍历,直到order为空为止
while order.size > 1:
temp = order[0]
res.append(temp)
# 计算当前概率最大矩形框与其他矩形框的相交框的坐标,会用到numpy的broadcast机制,得到的是向量
xx1 = np.maximum(x1[temp], x1[order[1:]])
yy1 = np.maximum(y2[temp], y1[order[1:]])
xx2 = np.minimum(x2[temp], x2[order[1:]])
yy2 = np.minimum(y2[temp], x2[order[1:]])
# 计算相交框的面积,注意矩形框不相交时w或h算出来会是负数,用0代替
w = np.maximum(0, xx2 - xx1 - 1)
h = np.maximum(0, yy2 - yy1 + 1)
in_areas = w * h
# 计算IOU
over = in_areas / (areas[temp] + areas[order[1:]] - in_areas)
indx = np.where(overIOU
在目标检测当中,有一个重要的概念就是 IOU。一般指代模型预测的 bbox 和 Groud Truth 之间的交并比。何为交并比呢?
![]()
相信这就很直观了具体的公式为:IOU=重合区域/(A面积+B面积-重合区域)具体代码如下所示:
def IOU(box1, box2):
'''
box1:左上角(box1[0],box1[1]) 右下角:(box1[2],box1[3])
box2:左上角(box2[0],box2[1]) 右下角:(box2[2],box2[3])
(box1)
1--------1
1 1----1------1
1---1----1 1
1 1
1-----------1 (box2)
'''
area1 = (box1[2]-box1[0])*(box1[3]-box1[1])
area2 = (box2[2]-box2[0])*(box2[3]-box2[1])
left = max(box1[0], box2[0])
right = min(box1[2], box2[2])
bottom = max(box1[1], box2[1])
top = min(box1[3], box2[3])
h = max(0, top-bottom)
w = max(0, right-left)
return (h*w)/(area2+area1-h*w)
if __name__ == '__main__':
rec_1 = (567, 45, 899, 89) #四个值分别为左上角顶点(x1,y1),右下角坐标(x2,y2)
rec_2 = (663, 56, 683, 87)
iou = IOU(rec_1, rec_2)
print(iou)