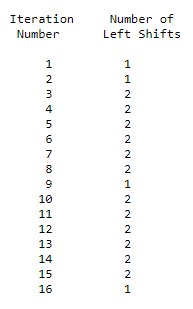des和aes相比较有哪些特点_第十七个知识点:描述和比较DES和AES的轮结构
第十七个知识点:描述和比较DES和AES的轮结构
这是密码学52件事中的第17篇.本周我们描述和比较DES和AES的结构.
DES和AES都是迭代分组密码的例子.分组密码通过重复使用一个简单的轮函数来得到它的安全性.轮函数得到一个n-bit的输入和返回一个n-bit的输出,其中n是密码块的大小.轮数r可以是可变的也可以是固定的.一般来说轮数的增加会增强块密码的安全水平.Round函数每轮使用的密钥都是从主密钥k获得的,使用密钥调度算法将k生成多个k分别使用在不同的轮.解密过程就试每轮的密钥都是可逆的,解密只需要反过来使用.在DES中,函数需要是不可逆的,但是整个函数是可逆的.对于AES(Rijndael)来说,不仅仅整个函数都是可逆的,每轮函数也都是可逆的.
DES
实际上,DES密码是Feistel密码的变种.Feistel密码有趣的属性就是每轮的轮函数都是可逆的,无论\(F\)怎么选择:
\[L_i = R_{i-1}
\]
\[R_i = L_{i-1} \oplus F(K_i,L_i)
\]
因此,解密形式就是
\[R_{i-1} = L_i
\]
\[L_{i-1} = R_i \oplus F(K_i,L_i)
\]
通过这种方法,我们可以为函数F选择任意的函数,并且我们仍然可以得到一个加密函数,它可以使用秘钥进行反转。加密和解密功能可以使用相同的代码/电路。我们只需要以相反的顺序使用圆形密钥来解密。作为Feistel密码设计的一个变体,DES具有以下明显的特点:
轮数r是16
块的长度是64bits
密钥长度是56bits
轮密钥\(K_1,K_2...K_16\)每个是48bits
在Feistel网络最开始和结束都使用了一个置换
总结一下DES密码对64位明文的加密操作:
执行一个初始的置换
将块的左半部分和右半部分分开
执行下面的步骤十六轮,每轮有六个步骤
扩展置换,右半部分的32bit被扩展成48bit
上面的48bit和密钥异或相乘得到48bit长的输出
将上面的48bit分割成8个6bit的值
S-Box:每6bit的值通过8个不同S-Box之一,产生4bit的输出.每个S-Box是一个四行六列的矩阵.六个输入和矩阵进行乘积,得到列.Bits 1和6生成行号,bits 2,3,4,5指定列号.最后S-Box的输出就是这个表中的元素
P-Box:我们现在有8个4bit的输出,把他们组合成一个32bit的值.然后用这个p-box置换,就得到了F的值
将另外半块加在一起
执行一个最终的置换
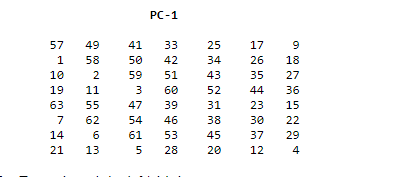
DES密钥调度算法接受56bit的密钥,这个56bit的密钥实际上是一个64bit的密钥,有8bit是校验位.首先最开始置换这个密钥(64bit输入同时56bit输出,因此丢失了奇偶校验位).然后用一个叫PC-1的矩阵来置换一下:
这样就从一个64bit的流中得到了一个56bit的输出.对这个56bit的输出,我们分割成左右两部分\(C_0,D_0\),每个有28bit,然后我们生成一些\(C_i,D_i\),其中\(1 \le i \le 16\).这个算法就是每次循环移动一位或者两位,具体按照下面的表格:
这样得到了16个\(C_i,D_i\).每对组合起来还是56bit,在分别用下面的PC-2来置换.生成48bit的密钥.
注意,对于许多现代应用程序来说,56位的密钥长度是不够的,因此通常使用DES时要使用三个密钥和主密码的三个迭代。这种版本称为三重DES或3DES。在3DES中键长等于168。还有另一种使用DES三次的方法,但是使用两个键而不是三个键,键长为112。在这个3DES的双键版本中,我们使用了3DES的基本结构,但是第一键和第三键是相等的。然而,双密钥3DES并不像人们最初认为的那样安全。
有关实际值(S-Boxes、P-Boxes和所有排列表)的更多细节可以在[1]中找到。
AES
AES算法,不像DES,是一个不依赖Feistel网络的块密码设计方案.然而AES和DES还是有很多相似的地方.它使用一个重复的轮数来获取安全性.每一轮由替换和置换,还有一个密钥叠加组成.AES有一个强数学结构,它的大部分操作都是基于\(GF(2^8)\)的.然而不像DES,加解密操作都是不同的.
AES在\(F_2^8[x]\)中用多项式识别32位的字.AES是参数化的,即可以使用128,192,256三种形式.对每一个形式,密钥长度和轮数都是不同的.
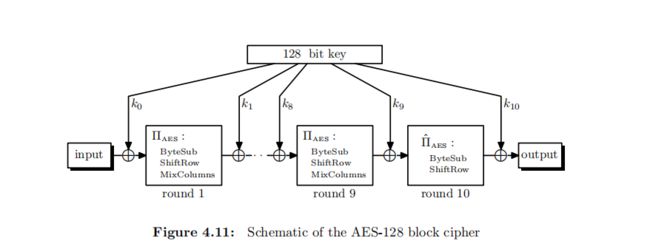
为了让我们的讨论更加简单,我们仅仅考虑10轮,128bit的情况.AES操作一个内部的4*4的矩阵(S(4,4)),称为状态矩阵.每轮密钥也是一个4*4的矩阵.AES使用下面四个操作.
下面是算法的伪代码:
AddRoundKey(S, K0)
for i = 1 to 9 do
SubBytes(S)
ShiftRows(S)
MixColumns(S)
AddRoundKey(S, Ki)
end
SubBytes(S)
ShiftRows(S)
AddRoundKey(S, K10)
下面是密钥扩展算法
W0 =K0,W1 =K1,W2 =K2,W3 =K3
for i = 1 to 10 do 
T = RotBytes(W4i−1)
T = SubBytes(T)
T = T ⊕ RCi
W4i = W4i−4 ⊕ T
W4i+1 = W4i−3 ⊕ W4i
W4i+2 = W4i−2 ⊕ W4i+1
W4i+3 = W4i−1 ⊕ W4i+2
end
\[K_i = (W_{i,0},W_{i,1},W_{i,2},W_{i,3})
\]
for all \(i\),\(0 \le i \le 10\)