数据结构——栈和队列
文章目录
- 一、数据结构简介
-
- 1、逻辑结构
- 2、存储（物理）结构
- 3、常见的数据结构
- 二、栈（stack）
-
- 1、 用数组实现栈
- 2、 用链表实现栈
- 3、 栈的应用举例——数制转换问题
- 三、 队列（queue）
-
- 1、用链表实现队列
- 2、用循环数组实现队列
- 补充拓展
一、数据结构简介
数据结构是计算机存储、组织数据的方式，指相互之间存在一种或多种特定关系的数据元素的集合，往往同高效的检索算法和索引技术有关。“结构”就是指数据元素之间存在的关系，分为逻辑结构和存储（物理）结构。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。
1、逻辑结构
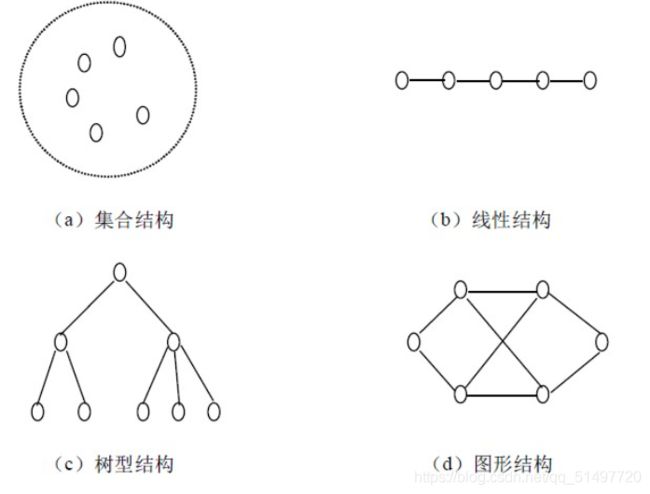
指反映数据元素之间的逻辑关系的数据结构，其中的逻辑关系是指数据元素之间的前后间关系，而与他们在计算机中的存储位置无关。一般分为线性和非线性两大类，或者以下四类：
- 集合结构：数据元素之间除了“属于同一个集合”的关系之外没有其他关系。
- 线性结构：数据元素的有序集合。数据元素之间形成一对一的关系。
- 树型结构：树是层次数据结构，树中数据元素之间存在一对多的关系。
- 图状结构：图中数据元素之间的关系是多对多的。
2、存储（物理）结构
指数据的逻辑结构在计算机存储空间中的存放形式。一般来说，一种数据结构的逻辑结构根据需要可以表示成多种存储结构，常用的存储结构有顺序存储、链式存储、索引存储和哈希存储等。
-
顺序存储结构是指用一组连续的存储单元一次存储数据元素，数据元素之间的逻辑关系是有元素的存储位置来（隐式）表示的。
-
链式存储结构是指用一组任意的存储单元来存储数据元素，数据元素之间的逻辑关系借助于指示元素存储地址的执指针来（显示）表示。
3、常见的数据结构
常用的数据结构有：数组，栈，链表，队列，树，图，堆，散列表（哈希表）等。
二、栈（stack）
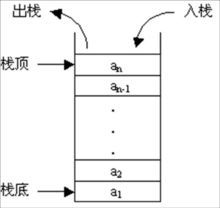
栈是一种特殊的线性表（0个或以上相同类型的数据元素构成的有限序列），仅能在线性表的一端操作，允许操作的一端叫栈顶，不允许的叫栈底。 栈的特点是：先进后出，从栈顶放入元素的操作叫入栈，取出元素叫出栈。
以java为例，要实现的栈的API如下：
public class Stack< Item> implements Iterable< Item>
Stack() —————————— 创建一个空栈
void push(Item item) ———— 添加一个元素
Item pop() —————————删除最近添加的元素
boolean isEmpty() ————— 栈是否为空
int size() ————————— 栈中的元素数量
1、 用数组实现栈
public class ArrayStack <Item>{
// 栈元素的总数
private int N = 0;
// 存放栈元素的数组
private Item [] items;
public ArrayStack (int M) {
items = (Item[]) new Object[M];
}
/**
* @description: 向栈顶插入元素
*/
public void push (Item item) {
if (N<=items.length)
items[N++] = item;
else System.out.println("栈已满");
}
/**
* @description: 从栈顶删除元素，并将删除的元素返回
*/
public Item pop () {
// 当栈还是空的时候， 不删除并且返回空
if(isEmpty()) return null;
// 保存将要被删除的元素
Item i = items[N-1];
// 将该元素删除
items[N-1] = null;
// 栈的长度减1
N--;
return i;
}
/**
* @description: 判断栈是否为空
*/
public boolean isEmpty () {
return N == 0;
}
/**
* @description: 返回栈的大小
*/
public int size () {
return N;
}
public static void main (String args []) {
// 开始时指定栈的容量为2
ArrayStack<Integer> stack = new ArrayStack(5);
//ArrayStack stack2 = new ArrayStack(5);
// 向栈顶依次添加4个元素
for(int i=1;i<5;i++)
stack.push(i);
// 依次从栈顶删除4个元素
for(int i=1;i<5;i++)
System.out.println(stack.pop());
System.out.println(stack.pop());
}
}
输出：
4
3
2
1
null
2、 用链表实现栈
public class LinkedListStack<Item> {
// 栈中元素的总数
private int N = 0;
// 链表头元素
private Node front;
// 内部结点类
private class Node {
Item item;
Node next;
}
/**
* @description: 向栈顶插入元素
*/
public void push (Item item) {
Node oldFront = front;
// 向链表头部插入新的结点
front = new Node();
front.item = item;
// 将新头结点的next指针指向旧的头结点
front.next = oldFront;
// 栈的长度加1
N++;
}
/**
* @description: 向栈顶删除元素，并将删除的元素返回
*/
public Item pop () {
// 当栈还是空的时候， 不删除并且返回空
if(isEmpty()) return null;
// 保存待删除的项以便返回
Item item = front.item;
// 删除原头结点
front = front.next;
// 栈的长度减1
N--;
return item;
}
/**
* @description: 判断栈是否为空
*/
public boolean isEmpty () {
return N == 0;
}
/**
* @description: 返回栈的大小
*/
public int size () {
return N;
}
public static void main (String args []) {
// 创建栈
LinkedListStack<Integer> stack = new LinkedListStack();
// 向栈顶依次添加4个元素
for(int i=1;i<5;i++)
stack.push(i);
// 依次从栈顶删除4个元素
for(int i=1;i<5;i++)
System.out.println(stack.pop());
}
}
输出：
4
3
2
1
null
3、 栈的应用举例——数制转换问题
问题：实现十进制数N和其他d进制数的转换
分析：
十进制数N和其他d进制数的转换解决方法很多，其中一个简单算法基于下列原理：
N=（N div d) * d+N mod d（其中：div 为整除运算，mod 为求余运算）
但计算过程是从低位到高位顺序产生d进制数的各个数位，而打印输出时，一般来说应从高位到低位进行，恰好和计算过程相反，所以此类问题适合用“先进后出"的栈来解决。
例如：（173）10=（10101101）2，其运算过程如下：
public static void main (String args []) {
// 创建栈
LinkedListStack stack = new LinkedListStack();
//输入十进制数num和要转换的d进制
Scanner in=new Scanner(System.in);
int num=in.nextInt();
int d=in.nextInt();
while (num!=0){
stack.push(num%d);
num=num/d;
}
while(!stack.isEmpty()){
System.out.print(stack.pop());
}
}
输出：
173
2
10101101
其他问题：表达式求值
中缀表达式、后缀表达式……
三、 队列（queue）
队列与栈一样，也是一种线性表，不同的是，队列可以在一端添加元素，在另一端取出元素，也就是：先进先出。把允许插入的一端称为队尾（rear），允许删除的一端称为队首（front），示例图如下：
要实现的栈的API如下：
public class Queue< Item> implements Iterable< Item>
Queue() ——————————— 创建一个空队列
void enqueue(Item item) ———— 向队尾添加一个元素
Item dequeue() ———————— 删除队首的元素
boolean isEmpty() ———————队列是否为空
int size() ———————————队列中的元素数量
1、用链表实现队列
public class LinkListQueue <Item>{
// 链表中的结点数目
private int N = 0;
// 链表头结点
private Node front = null;
// 链表尾结点
private Node rear = null;
// 结点内部类
private class Node {
Item item;
Node next;
}
/**
* @description: 元素入列（在链表尾部添加）
*/
public void enqueue (Item item) {
Node oldRear = rear;
rear = new Node();
rear.item = item;
if (isEmpty()) front = rear;
else oldRear.next = rear;
N++;
}
/**
* @description: 元素出列（在链表头部删除）
*/
public Item dequeue () {
if(isEmpty()) return null;
Item item = front.item;
front = front.next;
N--;
if(isEmpty()) rear = null;
return item;
}
/**
* @description: 判断队列是否为空
*/
public boolean isEmpty () {
return N == 0;
}
/**
* @description: 返回队列长度
*/
public int size () {
return N;
}
public static void main (String args []) {
LinkListQueue<String> queue = new LinkListQueue();
// 向队尾依次添加4个元素
for(int i=1;i<4;i++)
queue.enqueue("A");
queue.enqueue("B");
// 依次删除4个元素
for(int i=1;i<5;i++)
System.out.println(queue.dequeue());
}
}
输出：
A
A
A
B
2、用循环数组实现队列
Why??
因为仅靠普通的数组实现队列可能会导致一个问题：数组大量空位元素得不到利用。
代码如下图所示， 可以看到，实现循环的关键是使用的一个取余数的操作，使得指针在移动到数组尾部的时候，能够重新移动到数组的头部。
解决办法：
队首队尾加1后，与队列的容量进行“模运算”，以保证队首队尾在队列的有效下标范围内移动。
public class CircleArrayQueue<Item> {
// 队列元素总数
private int N = 0;
// 数组长度
private int M;
// 队列头部元素指针
private int front = 0;
// 队列尾部元素指针
private int rear = 0;
private Item [] items;
public CircleArrayQueue (int M) {
this.M = M;
items = (Item [])new Object[M];
}
/**
* @description: 入列操作
*/
public void enqueue (Item item) {
// 当队列为空时， 不能进行入列操作
if (isFull()) return;
// 向队列尾部插入元素
items[rear] = item;
// 用数组长度M取余， 使得rear到达数组尾部时能返回数组头部
rear = (rear + 1) % M;
// 增加队列长度
N++;
}
/**
* @description: 出列，并返回被删除项
*/
public Item dequeue () {
// 当队列为满时， 不能进行出列操作
if (isEmpty()) return null;
// 保存待删除元素， 以待返回
Item item = items[front];
// 删除队列头部元素
items[front] = null;
// 用数组长度M取余， 使得front到达数组尾部时能返回数组头部
front = (front + 1) % M;
// 减少队列长度
N--;
// 返回删除元素
return item;
}
/**
* @description: 判断队列是否满了
*/
public boolean isFull () {
return N == M;
}
/**
* @description: 判断队列是否为空
*/
public boolean isEmpty () {
return N == 0;
}
/**
* @description: 返回队列元素总数
*/
public int size () {
return N;
}
public static void main (String args []) {
CircleArrayQueue<Integer> queue = new CircleArrayQueue(3);
// 依次添加3个元素
for(int i=1;i<4;i++)
queue.enqueue(i);
// 依次删除3个元素
System.out.println("rear="+queue.rear);
for(int i=1;i<4;i++)
System.out.println(queue.dequeue());
}
}
输出：
rear=0
1
2
3
判断循环数组的满状态和空状态
在循环数组的实现中，一个非常重要的操作就是区分数组是处在"满"状态还是“空”状态，因为当front和rear指向同一个元素位置时，既可能处在满状态也可能处在空状态。上面的代码里我们是通过一个表示队列元素总数的变量N去判断的，除此之外，我们也可以通过另外一种不依赖于变量N的方式去判断数组的满和空的状态， 但代价是少用一个元素空间，例如：（其余代码同上）
public boolean isFull () {
return (rear + 1) % M == front;
}
public boolean isEmpty () {
return rear == front;
}
输出：
rear=2
1
2
null
补充拓展
链接: 堆、栈、堆栈和队列的区别.