详解一道高频面试题:接雨水
学算法认准 labuladong
后台回复 进群 进刷题
读完本文,可以去力扣解决如下题目:
42. 接雨水(困难)
![]()
接雨水这道题目挺有意思,在面试题中出现频率还挺高的,本文就来步步优化,讲解一下这道题。
先看一下题目:

就是用一个数组表示一个条形图,问你这个条形图最多能接多少水。
int trap(int[] height);下面就来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法,在 O(N) 时间 O(1) 空间内解决这个问题。
一、核心思路
所以对于这种问题,我们不要想整体,而应该去想局部;就像之前的文章写的动态规划问题处理字符串问题,不要考虑如何处理整个字符串,而是去思考应该如何处理每一个字符。
这么一想,可以发现这道题的思路其实很简单。具体来说,仅仅对于位置i,能装下多少水呢?
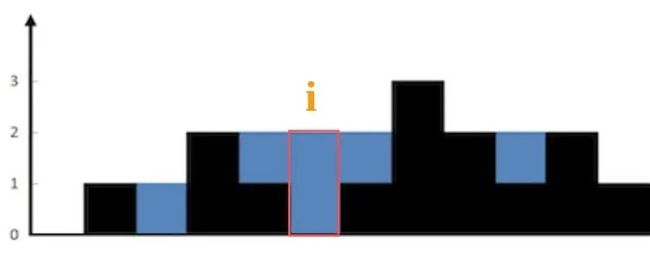
能装 2 格水,因为height[i]的高度为 0,而这里最多能盛 2 格水,2-0=2。
为什么位置i最多能盛 2 格水呢?因为,位置i能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关,我们分别称这两个柱子高度为l_max和r_max;位置 i 最大的水柱高度就是min(l_max, r_max)。
更进一步,对于位置i,能够装的水为:
water[i] = min(
# 左边最高的柱子
max(height[0..i]),
# 右边最高的柱子
max(height[i..end])
) - height[i]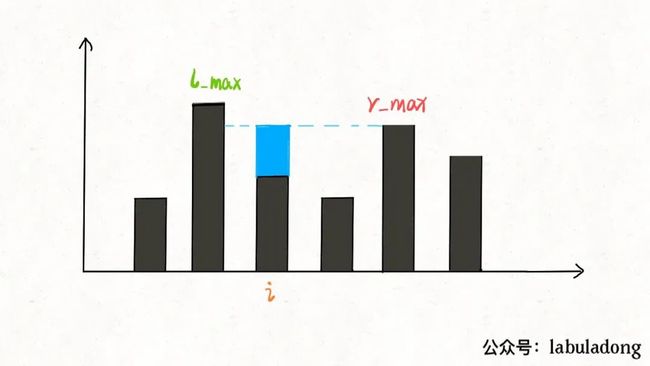

这就是本问题的核心思路,我们可以简单写一个暴力算法:
int trap(int[] height) {
int n = height.length;
int res = 0;
for (int i = 1; i < n - 1; i++) {
int l_max = 0, r_max = 0;
// 找右边最高的柱子
for (int j = i; j < n; j++)
r_max = Math.max(r_max, height[j]);
// 找左边最高的柱子
for (int j = i; j >= 0; j--)
l_max = Math.max(l_max, height[j]);
// 如果自己就是最高的话,
// l_max == r_max == height[i]
res += Math.min(l_max, r_max) - height[i];
}
return res;
}有之前的思路,这个解法应该是很直接粗暴的,时间复杂度 O(N^2),空间复杂度 O(1)。但是很明显这种计算r_max和l_max的方式非常笨拙,一般的优化方法就是备忘录。
二、备忘录优化
之前的暴力解法,不是在每个位置i都要计算r_max和l_max吗?我们直接把结果都提前计算出来,别傻不拉几的每次都遍历,这时间复杂度不就降下来了嘛。
我们开两个数组r_max和l_max充当备忘录,l_max[i]表示位置i左边最高的柱子高度,r_max[i]表示位置i右边最高的柱子高度。预先把这两个数组计算好,避免重复计算:
int trap(int[] height) {
if (height.length == 0) {
return 0;
}
int n = height.length;
int res = 0;
// 数组充当备忘录
int[] l_max = new int[n];
int[] r_max = new int[n];
// 初始化 base case
l_max[0] = height[0];
r_max[n - 1] = height[n - 1];
// 从左向右计算 l_max
for (int i = 1; i < n; i++)
l_max[i] = Math.max(height[i], l_max[i - 1]);
// 从右向左计算 r_max
for (int i = n - 2; i >= 0; i--)
r_max[i] = Math.max(height[i], r_max[i + 1]);
// 计算答案
for (int i = 1; i < n - 1; i++)
res += Math.min(l_max[i], r_max[i]) - height[i];
return res;
}这个优化其实和暴力解法思路差不多,就是避免了重复计算,把时间复杂度降低为 O(N),已经是最优了,但是空间复杂度是 O(N)。下面来看一个精妙一些的解法,能够把空间复杂度降低到 O(1)。
三、双指针解法
这种解法的思路是完全相同的,但在实现手法上非常巧妙,我们这次也不要用备忘录提前计算了,而是用双指针边走边算,节省下空间复杂度。
首先,看一部分代码:
int trap(int[] height) {
int left = 0, right = height.length - 1;
int l_max = 0, r_max = 0;
while (left < right) {
l_max = Math.max(l_max, height[left]);
r_max = Math.max(r_max, height[right]);
// 此时 l_max 和 r_max 分别表示什么?
left++; right--;
}
}对于这部分代码,请问l_max和r_max分别表示什么意义呢?
很容易理解,l_max是height[0..left]中最高柱子的高度,r_max是height[right..end]的最高柱子的高度。
明白了这一点,直接看解法:
int trap(int[] height) {
int left = 0, right = height.length - 1;
int l_max = 0, r_max = 0;
int res = 0;
while (left < right) {
l_max = Math.max(l_max, height[left]);
r_max = Math.max(r_max, height[right]);
// res += min(l_max, r_max) - height[i]
if (l_max < r_max) {
res += l_max - height[left];
left++;
} else {
res += r_max - height[right];
right--;
}
}
return res;
}你看,其中的核心思想和之前一模一样,换汤不换药。但是细心的读者可能会发现次解法还是有点细节差异:
之前的备忘录解法,l_max[i]和r_max[i]分别代表height[0..i]和height[i..end]的最高柱子高度。
res += Math.min(l_max[i], r_max[i]) - height[i];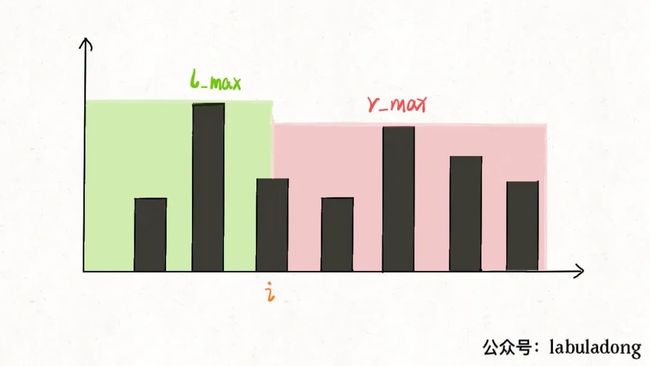
但是双指针解法中,l_max和r_max代表的是height[0..left]和height[right..end]的最高柱子高度。比如这段代码:
if (l_max < r_max) {
res += l_max - height[left];
left++;
}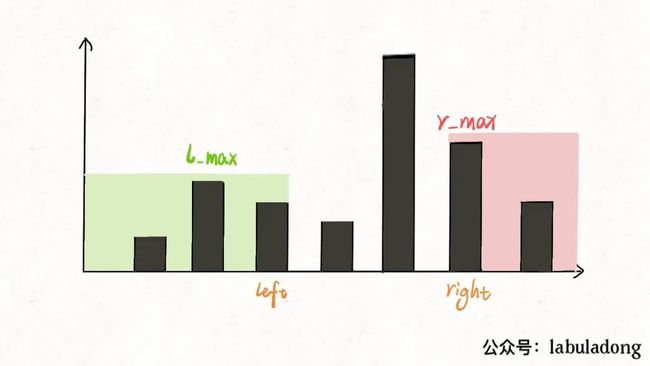
此时的l_max是left指针左边的最高柱子,但是r_max并不一定是left指针右边最高的柱子,这真的可以得到正确答案吗?
其实这个问题要这么思考,我们只在乎min(l_max, r_max)。对于上图的情况,我们已经知道l_max < r_max了,至于这个r_max是不是右边最大的,不重要。重要的是height[i]能够装的水只和较低的l_max之差有关:
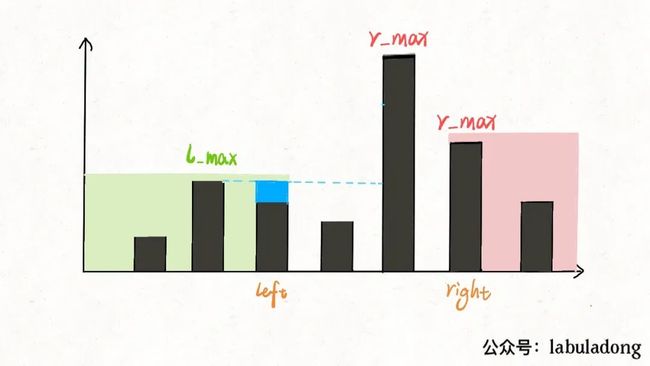
这样,接雨水问题就解决了。
扩展延伸
下面我们看一道和接雨水问题非常类似的题目,力扣第 11 题「盛最多水的容器」:

函数签名如下:
int maxArea(int[] height);这题和接雨水问题很类似,可以完全套用前文的思路,而且还更简单。两道题的区别在于:
接雨水问题给出的类似一幅直方图,每个横坐标都有宽度,而本题给出的每个横坐标是一条竖线,没有宽度。
我们前文讨论了半天l_max和r_max,实际上都是为了计算height[i]能够装多少水;而本题中height[i]没有了宽度,那自然就好办多了。
举个例子,如果在接雨水问题中,你知道了height[left]和height[right]的高度,你能算出left和right之间能够盛下多少水吗?
不能,因为你不知道left和right之间每个柱子具体能盛多少水,你得通过每个柱子的l_max和r_max来计算才行。
反过来,就本题而言,你知道了height[left]和height[right]的高度,能算出left和right之间能够盛下多少水吗?
可以,因为本题中竖线没有宽度,所以left和right之间能够盛的水就是:
min(height[left], height[right]) * (right - left)类似接雨水问题,高度是由height[left]和height[right]较小的值决定的。
解决这道题的思路依然是双指针技巧:
用left和right两个指针从两端向中心收缩,一边收缩一边计算[left, right]之间的矩形面积,取最大的面积值即是答案。
先直接看解法代码吧:
int maxArea(int[] height) {
int left = 0, right = height.length - 1;
int res = 0;
while (left < right) {
// [left, right] 之间的矩形面积
int cur_area = Math.min(height[left], height[right]) * (right - left);
res = Math.max(res, cur_area);
// 双指针技巧,移动较低的一边
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return res;
}代码和接雨水问题大致相同,不过肯定有读者会问,下面这段 if 语句为什么要移动较低的一边:
// 双指针技巧,移动较低的一边
if (height[left] < height[right]) {
left++;
} else {
right--;
}其实也好理解,因为矩形的高度是由min(height[left], height[right])即较低的一边决定的:
你如果移动较低的那一边,那条边可能会变高,使得矩形的高度变大,进而就「有可能」使得矩形的面积变大;相反,如果你去移动较高的那一边,矩形的高度是无论如何都不会变大的,所以不可能使矩形的面积变得更大。
至此,这道题也解决了。
_____________
最后,没关注我视频号的读者赶紧关注下,每周末有空直播: