动态规划算法解决背包问题(Java实现)
文章收藏的好句子:你在书本上花的任何时间,都会在某一个时刻给你回报。
目录
1、动态规划算法的概述
2、背包问题
3、动态规划算法解决背包问题
3、1 不可重复装入商品
3、2 思路分析
1、动态规划算法的概述
(1)动态规划算法的思想是:将大问题分为小问题进行解决,使得一步步获得最优解的处理算法。
(2)动态规范算法与分治算法很类似,思想都是以待解决问题先分解成 n 个子问题,先求解子问题,然后从子问题中得到原问题的解。
(3)动态规划求解的问题与分治算法不同的点在于,经过分解出来的子问题不是相互独立的,下一个子问题的求解是建立在上一个子问题解决的求解基础上的,依次递进获取最终解。
(4)动态规划可以通过填表的方式一步步推进,最终得到最优解。
2、背包问题
这里就有一个背包问题了,有一个容量为4磅的背包,需要装入如下表1的物品,怎样才能使装入包中的商品最值钱且不超过4磅重?
3、动态规划算法解决背包问题
上面的背包问题,放入商品的总质量不能超过4磅且要实现背包装入商品价值的最大化,这里假设放入的商品是不能重复的, 可用一个二维表格来表示。
3、1 不可重复装入商品
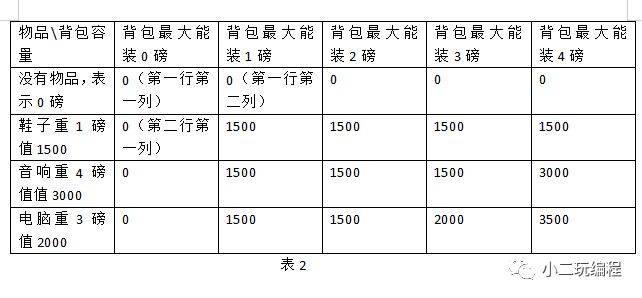
我先画一个表格2,然后会对这个表格2进行详细的说明,如下所示;
说明:列表示背包能装多大的重量,横表示物品的类型和商品数量,行和列交叉而出现的数据表示背包能装的物品总和的最大价值。
好,我们现在对表2的数据分析一下,第一行的数据全部为0,这个可以理解吧?不管背包能放多大的重量,只要不放入物品,那就是0咯;第一列的数据全部为0,是因为背包能装0磅;我们看第二行第二列的数据到第二行第五列的数据,首先第二行能放的物品只能是鞋子且不能重复对不对?那不管背包(装的重量大于等于1磅)能装多少磅的物品,都是只能放1磅的鞋子对不对?那自然就是1500了。
我们看第三行第二列到第三行第五列的数据,第三行能放入的物品是鞋子、音响且同一个物品不能放超过1个,第三行的第二列到第三行的第四列只能放1磅的鞋子,放不下音响(音响4磅重),所以就是1500了,而第三行的第五列刚好能放4磅的音响,而且放一个音响比放一双鞋子更值钱对不对?
第四行可以放的商品有鞋子、音响和电脑,好,现在看第四行的第二列到第四行的第三列,由于第二列和第三列是只能装1磅和2磅对不对?那就只能放一双鞋子了,所以就是1500了;第四行的第四列能装3磅,那就是可以放一双鞋子或者一台电脑,由于电脑比鞋子更值钱对不对,所以放电脑更好点,所以就是2000了;看第四行的第五列,背包可以装4磅,那这里面就有较好一点的两种方案选择了,一种是放一双鞋子和一台电脑,另一种是只放一台音响,一看放一双鞋子和一台电脑的方案更值钱对不对,所以是1500+2000就是3500了。
从表2可以小结一下
(1)横行表示背包容量从0到指定容量的各种情况,这是第一步的分,将大容量的背包先转化为小容量背包,算出子问题的最优解,然后一步步加大容量,算出最终问题的最优解。
(2)纵行表示商品信息,且第一横行为空值,作为初始数据的对比值;纵行是第二步的分,先将一个商品放入背包中,算出最优解,逐渐增加商品类型和商品数量,算出最终最优解。
(3)最终表格的最右下角的格子,即为数据的最优解;看表2最右下角的数据3500,是不是最优解。
3、2 思路分析
(1)利用动态规划来解决,假设给定的 n 个物品,设 v[i]、 w[i] 分 别为第 i 个商品的价值和重量,C 为背包的容量。
(2)每次遍历到的第 i 个商品,根据 w[i] 和 v[i] 来确定是否需要将该商品放入背包中;这句话说的是什么意思呢?我举个例子,你们就理解了,看表2的第四行的第四列的2000这个数据,首先第四列背包最大容量是3磅对不对?第四行能放的商品有鞋子、音响和电脑对不对?但是音响比背包的容量更大,所以就只能放鞋子和电脑,鞋子和电话的重量和超过3磅对不对,所以又只能从鞋子和电脑里面挑选一个放进去,由于电脑比鞋子更值钱对不对?所以放电脑价值更大对不对?所以是根据 w[i] 和 v[i] 来确定是否需要将该商品放入背包中。
(3)再令 v[i][j] 表示在前 i 个商品中能够装入容量为 j 的背包中的最大价值;这句话又是什么意思啊?我再举个例子,看表2的第三行第五列的3000,这时候 i 就是2,j 就是4,v[i][j] 就是 v[2][4],也就是 v[2][4] 为3000;第二行只能装的商品是鞋子对不对?第三行能装入的商品包含第二行装入的商品,也就是说第三行能选择装入的商品是鞋子和音响;如果鞋子和音响同时放入背包(背包容量为4磅,j=4)肯定是装不下的对不对?所以从鞋子和音响里面选最值钱的放入背包中,所以就是 v[i][j] 表示在前 i 个商品中能够装入容量为 j 的背包中的最大价值。
现在我们从思路分析和表2中能够总结出以下几条公式;
(1)v[i][0] = v[0][j] = 0,其中 i 表示第几行,j 表示第几列;看表2,第一列的数据是不是0?第一行的数据是不是也是0?
(2)当 w[i] > j 时,有 v[i][j] = v[i-1][j],w 表示第 i+1 行商品的重量 ;举例:看表2中的第三行的第二列,i = 2,w[i] = 4,j = 1,v[2][1] = v[2-1][1] = 1500 。
(3)当j >= w[i] 时,有 v[i][j]=max{v[i-1][j],v[i-1][j-w[i]]+v[i]} ,v[i] 表示第 i+1 行商品的价格;举例:看表2,看第四行的第五列数据,j = 4,i = 3,w[3] = 3,v[3] = 2000,那么 v[3][4] = max{v[3-1][4] , v[3-1][4-w[3]]+v[3]} = max{3000 , 3500},所以 v[3][4] = 3500 。
好,我们现在用代码实现一把;
(1)新建一个 Test 类:
package com.xiaoer.demo;
/**
* 动态规划: 背包问题
**/
public class Test {
public static void main(String[] args) {
Test test = new Test();
// 商品名字数组
String[] nameArr = {"鞋子", "音响", "电脑"};
// 商品重量数组
int[] weightArr = {1/*鞋子*/, 4/*音响*/, 3/*电脑*/};
// 商品价格数组
int[] priceArr = {1500/*鞋子*/, 3000/*音响*/, 2000/*电脑*/};
// 背包容量
int packageCapacity = 4;
// 把不可重复的商品装入背包
test.backpackWithoutRepeat(nameArr, weightArr, priceArr, packageCapacity);
}
/**
* 装入背包
* @param nameArr 商品名字数组
* @param w 商品重量数组
* @param priceArr 商品价格数组
* @param packageCapacity 背包容量
*/
private void backpackWithoutRepeat(String[] nameArr, int[] w, int[] priceArr, int packageCapacity) {
/**
* 声明一个能装入 0、1、2、3磅......的背包的二维价格表;举例:就好比 v数组是表2的数据
*/
int[][] v = new int[nameArr.length + 1][packageCapacity + 1];
// 构建可能装入背包的二维数组
// 值为0时说明不会装进背包, 值为1说明可能装入背包
int[][] contentArr = new int[nameArr.length + 1][packageCapacity + 1];
/**
* 为什么i一开始是1不是0?看表2的数据,是不是第一行全是0啊
*/
for (int i = 1; i < v.length; i++) {
/**
* 为什么j一开始是1不是0?看表2的数据,是不是第一列全是0啊
*/
for (int j = 1; j < v[i].length; j++) {
/**
* 文章中当 w[i] > j 时,就有 v[i][j] = v[i-1][j];
* 因为我们程序i是从1开始的,因此原来公式中的w[i]修改成w[i-1];
* 当前商品 > 背包容量, 取同列上一行数据
*/
if (w[i - 1] > j) {
v[i][j] = v[i - 1][j];
} else {
/**
* 当前商品 <= 背包容量, 对两部分内容进行比较;
* 第一部分, 该列上一行数据
*/
int onePart = v[i - 1][j];
/**
* 还记得文章中写的 当j >= w[i] 时,有 v[i][j]=max{v[i-1][j],v[i-1][j-w[i]]+v[i]} 这个公式成立吗?
* priceArr[i - 1]: 当前商品价格;
* w[i - 1]: 当前商品重量;
* j - w[i - 1]: 去掉当前商品, 背包剩余容量;
* 不可重复: v[i - 1][j - w[i - 1]]: 在上一行, 取剩余重量下的价格最优解;
*/
int otherPart = priceArr[i - 1] + v[i - 1][j - w[i - 1]];
/**
* 取最大值为当前位置的最优解
*/
v[i][j] = Math.max(onePart, otherPart);
/**
* 如果最优解包含当前商品, 则表示当前商品已经被使用, 进行记录
*/
if (otherPart == v[i][j]) {
contentArr[i][j] = 1;
}
}
}
}
// 不能重复的场景中
// 如果该位置的标志位为1, 说明该商品参与了最终的背包添加
// 如果该位置的标志位为0, 即使该位置的价格为最大价格, 也是从其他位置引用的价格
// 因为不能重复, 所以每行只取一个数据参与最终计算, 并只判断在最大位置该商品是否参与
// 该最大位置会随着已经遍历出其他元素而对应不断减小, 直到为0
// 二维数组最后一个元素必然是最大值, 但是需要知道该最大值是自身计算的 还是比较后引用其他的
int totalPrice = 0;
// 最大行下标数, 即商品数
int maxLine = contentArr.length - 1;
// 最大列下标数, 即重量
int maxColumn = contentArr[0].length - 1;
for (;maxLine > 0 && maxColumn > 0;) {
// 等于1表示在该位置该商品参与了计算
if (contentArr[maxLine][maxColumn] == 1) {
// 遍历后, 对重量减少, 下一次从剩余重量中取参与商品
maxColumn -= w[maxLine - 1];
totalPrice += priceArr[maxLine - 1];
System.out.println(nameArr[maxLine - 1] + "加入了背包");
}
// 因为不能重复
// 所以如果该商品参与了背包容量, 则肯定剩余的最大位置处参与,
// 否则跟该数据无关, 直接跳过
maxLine--;
}
System.out.println("背包可容纳的最大价值: " + totalPrice);
}
}程序运行结果如下所示;