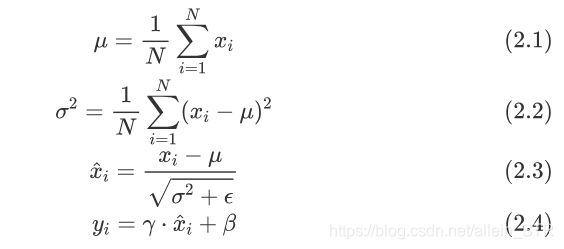Batch Normalization深入理解

Batch Normalization深入理解

1. BN的提出背景是什么？

统计学习中的一个很重要的假设就是输入的分布是相对稳定的。如果这个假设不满足，则模型的收敛会很慢，甚至无法收敛。所以，对于一般的统计学习问题，在训练前将数据进行归一化或者白化（whitening）是一个很常用的trick。

但这个问题在深度神经网络中变得更加难以解决。在神经网络中，网络是分层的，可以把每一层视为一个单独的分类器，将一个网络看成分类器的串联。这就意味着，在训练过程中，随着某一层分类器的参数的改变，其输出的分布也会改变，这就导致下一层的输入的分布不稳定。分类器需要不断适应新的分布，这就使得模型难以收敛。

对数据的预处理可以解决第一层的输入分布问题，而对于隐藏层的问题无能为力，这个问题就是Internal Covariate Shift。而Batch Normalization其实主要就是在解决这个问题。

除此之外，一般的神经网络的梯度大小往往会与参数的大小相关（仿射变换），且随着训练的过程，会产生较大的波动,这就导致学习率不宜设置的太大。Batch Normalization使得梯度大小相对固定，一定程度上允许我们使用更高的学习率。

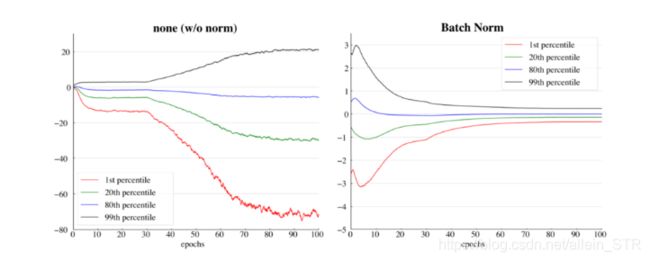
(左)没有任何归一化，(右)应用了batch normalization

2. BN工作原理是什么？

假定我们的输入是一个大小为 N 的mini-batch ，通过下面的四个式子计算得到的y  就是Batch Normalization(BN)的值

数据看起来像高斯分布。

首先，由(2.1)和(2.2)得到mini-batch的均值和方差，之后进行(2.3)的归一化操作，在分母加上一个小的常数是为了避免出现除0操作.整个过程中，只有最后的(2.4)引入了额外参数γ和β，他们的size都为特征长度，与 xi 相同。

BN层通常添加在隐藏层的激活函数之前，线性变换之后。如果我们把(2.4)和之后的激活函数放在一起看，可以将他们视为一层完整的神经网络（线性+激活）。（注意BN的线性变换和一般隐藏层的线性变换仍有区别，前者是element-wise的，后者是矩阵乘法。）

此时，  可以视为这一层网络的输入，而  是拥有固定均值和方差的。这就解决了Covariate Shift.

另外，  y还具有保证数据表达能力的作用。 在normalization的过程中，不可避免的会改变自身的分布，而这会导致学习到的特征的表达能力有一定程度的丢失。通过引入参数γ和β，极端情况下，网络可以将γ和β训练为原分布的标准差和均值来恢复数据的原始分布。这样保证了引入BN，不会使效果更差。

3. BN实现方法是什么？

我们将Batch Normalization分成正向（只包括训练）和反向两个过程。

正向过程的参数x是一个mini-batch的数据，gamma和beta是BN层的参数，bn_param是一个字典，包括  的取值和用于inference的 和 的移动平均值，最后返回BN层的输出y，会在反向过程中用到的中间变量cache，以及更新后的移动平均。

反向过程的参数是来自上一层的误差信号dout，以及正向过程中存储的中间变量cache，最后返回   的偏导数。

实现与推导的不同在于，实现是对整个batch的操作。

import numpy as np

def batchnorm_forward(x, gamma, beta, bn_param):
    # read some useful parameter
    N, D = x.shape
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    # BN forward pass
    sample_mean = x.mean(axis=0)
    sample_var = x.var(axis=0)
    x_ = (x - sample_mean) / np.sqrt(sample_var + eps)
    out = gamma * x_ + beta

    # update moving average
    running_mean = momentum * running_mean + (1-momentum) * sample_mean
    running_var = momentum * running_var + (1-momentum) * sample_var
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    # storage variables for backward pass
    cache = (x_, gamma, x - sample_mean, sample_var + eps)

    return out, cache


def batchnorm_backward(dout, cache):
    # extract variables
    N, D = dout.shape
    x_, gamma, x_minus_mean, var_plus_eps = cache

    # calculate gradients
    dgamma = np.sum(x_ * dout, axis=0)
    dbeta = np.sum(dout, axis=0)

    dx_ = np.matmul(np.ones((N,1)), gamma.reshape((1, -1))) * dout
    dx = N * dx_ - np.sum(dx_, axis=0) - x_ * np.sum(dx_ * x_, axis=0)
    dx *= (1.0/N) / np.sqrt(var_plus_eps)

    return dx, dgamma, dbeta

 

4. BN优点是什么？

• 更快的收敛。

• 降低初始权重的重要性。

• 鲁棒的超参数。

• 需要较少的数据进行泛化。

5. BN缺点是什么？

• 在使用小batch size的时候不稳定： batch normalization必须计算平均值和方差，以便在batch中对之前的输出进行归一化。如果batch大小比较大的话，这种统计估计是比较准确的，而随着batch大小的减少，估计的准确性持续减小。

以上是ResNet-50的验证错误图。可以推断，如果batch大小保持为32，它的最终验证误差在23左右，并且随着batch大小的减小，误差会继续减小(batch大小不能为1，因为它本身就是平均值)。损失有很大的不同(大约10%)。

如果batch大小是一个问题，为什么我们不使用更大的batch？我们不能在每种情况下都使用更大的batch。在finetune的时候，我们不能使用大的batch，以免过高的梯度对模型造成伤害。在分布式训练的时候，大的batch最终将作为一组小batch分布在各个实例中。

• 导致训练时间的增加：NVIDIA和卡耐基梅隆大学进行的实验结果表明，“尽管Batch Normalization不是计算密集型，而且收敛所需的总迭代次数也减少了。”但是每个迭代的时间显著增加了，而且还随着batch大小的增加而进一步增加。

batch normalization消耗了总训练时间的1/4。原因是batch normalization需要通过输入数据进行两次迭代，一次用于计算batch统计信息，另一次用于归一化输出。

• 训练和推理时不一样的结果：例如，在真实世界中做“物体检测”。在训练一个物体检测器时，我们通常使用大batch(YOLOv4和Faster-RCNN都是在默认batch大小= 64的情况下训练的)。但在投入生产后，这些模型的工作并不像训练时那么好。这是因为它们接受的是大batch的训练，而在实时情况下，它们的batch大小等于1，因为它必须一帧帧处理。考虑到这个限制，一些实现倾向于基于训练集上使用预先计算的平均值和方差。另一种可能是基于你的测试集分布计算平均值和方差值。

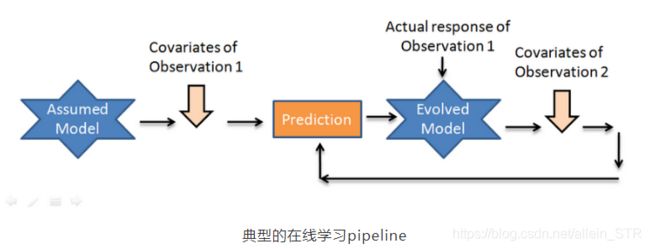
• 对于在线学习不好：在线学习是一种学习技术，在这种技术中，系统通过依次向其提供数据实例来逐步接受训练，可以是单独的，也可以是通过称为mini-batch的小组进行。每个学习步骤都是快速和便宜的，所以系统可以在新的数据到达时实时学习。

由于它依赖于外部数据源，数据可能单独或批量到达。由于每次迭代中batch大小的变化，对输入数据的尺度和偏移的泛化能力不好，最终影响了性能。

• 对于循环神经网络不好：

  虽然batch normalization可以显著提高卷积神经网络的训练和泛化速度，但它们很难应用于递归结构。batch normalization可以应用于RNN堆栈之间，其中归一化是“垂直”应用的，即每个RNN的输出。但是它不能“水平地”应用，例如在时间步之间，因为它会因为重复的重新缩放而产生爆炸性的梯度而伤害到训练。

  [^注]: 一些研究实验表明，batch normalization使得神经网络容易出现对抗漏洞，但我们没有放入这一点，因为缺乏研究和证据。

6. 可替换的方法：

在batch normalization无法很好工作的情况下，有几种替代方法。

• Layer Normalization

• Instance Normalization

• Group Normalization (+ weight standardization)

• Synchronous Batch Normalization

7.参考资料

1. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

2. Deriving the Gradient for the Backward Pass of Batch Normalization

3. CS231n Convolutional Neural Networks for Visual Recognition

4. https://towardsdatascience.com/curse-of-batch-normalization-8e6dd20bc304