python实现语音信号的分帧、加窗、预处理

音频文件读取

librosa是非常强大的python语音信号处理库。
读取音频：
使用语句librosa.load(path, sr=22050, mono=True, offset=0.0, duration=None)读取音频文件，默认的采样率是22050，若要保留音频的原始采样率，使用sr=None。

其中：
path：表示音频文件的路径
sr：表示采样率
mono：bool，是布尔类型，表示是否将信号转换为单声道
offset：float，后面跟的是浮点型，表示在此时间之后开始阅读（以秒为单位）
duration：float，表示的是持续时间，也就是只加载这么长的音频（单位为秒）
y：返回的y值表示音频时间序列
sr：表示的是音频的采样率

读取音频时长：
语句librosa.get_duration(y=None, sr=8000, S=None, n_fft=2048, hop_length=512, center=True, filename=None)来计算时间序列的持续时间（单位为秒）。
其中：
y：音频时间序列
sr：y的音频采样率
S：STFT矩阵或任何STFT衍生的矩阵(例如，色谱图或梅尔频谱图)
n_fft：S的 FFT窗口大小
hop_length：S列之间的音频样本数
center ：布尔值，如果为True，则S [:, t]的中心为y [t * hop_length]；如果为False，则S [:, t]从y[t * hop_length]开始
filename：如果提供，则所有其他参数都将被忽略，并且持续时间是直接从音频文件中计算得出的，返回的是持续时间（单位为秒）（librosa.get_duration(filename=’path’)）

如以音频文件bluesky1.wav文件为例，使用python读取音频文件：

# 读取音频文件

import numpy as np
import librosa.display  # 导入音频及绘图显示包
import matplotlib.pyplot as plt  # 导入绘图工作的函数集合

# 读取语音文件并绘制波形图
times = librosa.get_duration(filename='D:\任务\Bluesky1.wav')  # 获取音频时长
# 返回音频采样数组及采样率
y, sr = librosa.load('D:\任务\Bluesky1.wav', sr=8000, offset=0.0, duration=None)
x = np.arange(0, times, 1/sr)  # 时间刻度
plt.plot(x, y)
plt.xlabel('times')  # x轴时间
plt.ylabel('amplitude')  # y轴振幅
plt.title('bluesky1.wav', fontsize=12, color='black')  # 标题名称、字体大小、颜色
plt.show()

读取之后的结果：

预加重

信号分析中采用的预加重技术，就是在对信号取样以后，插入一个一阶的高通滤波器，使声门脉冲的影响减到最小，只剩下声道部分。也就是对语音信号进行高频提升，用一阶FIR滤波器表示：
$$s^{{}^{\prime }}(n)=s(n)－as(n－1)(a为常数)$$
预加重的作用：
增加一个零点，抵消声门脉冲引起的高端频谱幅度下跌，使信号频谱变得平坦及各共振幅度相接近，语音中只剩下声道中的影响，所提取的特征更加符合元声道的模型。

插入一个一阶高通滤波器，把高频提升的同时也把低频部分也进行了衰减，使有些基频赋值较大时，通过预加重后，降低基频对共振峰检测的干扰，同时也减少了频谱的动态范围。
程序代码：

'''预加重'''
# 读取音频文件
import numpy as np
import librosa.display  # 导入音频及绘图显示包
import matplotlib.pyplot as plt  # 导入绘图工作的函数集合
# 读取语音文件并绘制波形图
times = librosa.get_duration(filename='D:\任务\Bluesky1.wav')  # 获取音频时长
# 返回音频采样数组及采样率
y, sr = librosa.load('D:\任务\Bluesky1.wav', sr=8000, offset=0.0, duration=None)
x = np.arange(0, times, 1/sr)  # 时间刻度
plt.plot(x, y)
plt.xlabel('times')  # x轴时间
plt.ylabel('amplitude')  # y轴振幅
plt.title('bluesky1.wav', fontsize=12, color='black')  # 标题名称、字体大小、颜色
plt.show()

# 预加重
def pre_fun(x):  # 定义预加重函数
    signal_points=len(x)  # 获取语音信号的长度
    signal_points=int(signal_points)  # 把语音信号的长度转换为整型
    # s=x  # 把采样数组赋值给函数s方便下边计算
    for i in range(1, signal_points, 1):# 对采样数组进行for循环计算
        x[i] = x[i] - 0.98 * x[i - 1]  # 一阶FIR滤波器
    return x  # 返回预加重以后的采样数组
pre_emphasis = pre_fun(y)  # 函数调用
plt.plot(x, pre_emphasis)  # 绘出图形
plt.xlabel('times')  # x轴时间
plt.ylabel('amplitude')  # y轴振幅
plt.title('pre_emphasis-bluesky1.wav', fontsize=12, color='black')  # 标题名称、字体大小、颜色
plt.show()  # 显示

预加重以后的图像：

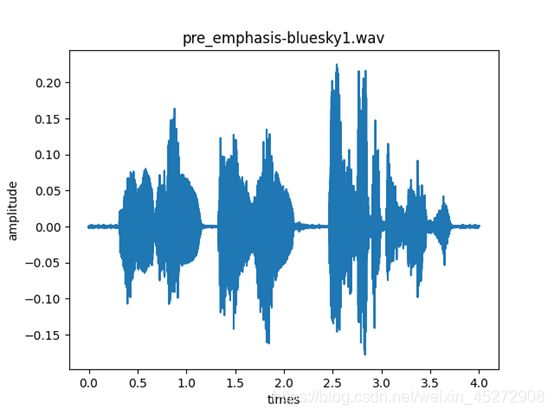
可以看出预加重以后的图像与原图像相比较，原图像的幅值很大，在预加重以后的频谱中，对基频谱线幅值有一定的抑制，高频端的幅值有所提升。

分帧

分帧就是将原始语音信号分成大小固定的N段语音信号，这里每一段语音信号都被称为一帧，帧长一般取10到30ms。分帧一般采用交叠分段的方法，是为了使帧与帧之间平滑过渡，保持其连续性。前一帧和后一帧的交叠部分称为帧移，帧移与帧长的比值一般取为0-1/2。

对于长为N的语音信号进行分帧：
$$f_n=\frac{N-lframe}{mframe}+1$$
数据将会被分成fn帧，每一帧在数据y中的位置为：

startindex = (0 ~ (fn - 1)) * inc +1

我们对一段语音进行分帧操作：

'''分帧'''
import numpy as np
import librosa.display  # 导入音频及绘图显示包
import matplotlib.pyplot as plt  # 导入绘图工作的函数集合

# 读取音频文件
# 读取语音文件并绘制波形图
times = librosa.get_duration(filename='D:\任务\Bluesky1.wav')  # 获取音频时长
# 返回音频采样数组及采样率
y, sr = librosa.load('D:\任务\Bluesky1.wav', sr=8000, offset=0.0, duration=None)
x = np.arange(0, times, 1/sr)  # 时间刻度
# 绘制图形
plt.plot(x, y)
plt.xlabel('times')  # x轴时间
plt.ylabel('amplitude')  # y轴振幅
plt.title('bluesky1.wav', fontsize=12, color='black')  # 标题名称、字体大小、颜色
plt.show()

# 分帧
def frame(x, lframe, mframe):  # 定义分帧函数
    signal_length = len(x)  # 获取语音信号的长度
    fn = (signal_length-lframe)/mframe  # 分成fn帧
    fn1 = np.ceil(fn)  # 将帧数向上取整，如果是浮点型则加一
    fn1 = int(fn1)  # 将帧数化为整数
    # 求出添加的0的个数
    numfillzero = (fn1*mframe+lframe)-signal_length
    # 生成填充序列
    fillzeros = np.zeros(numfillzero)
    # 填充以后的信号记作fillsignal
    fillsignal = np.concatenate((x,fillzeros))  # concatenate连接两个维度相同的矩阵
    # 对所有帧的时间点进行抽取，得到fn1*lframe长度的矩阵d
    d = np.tile(np.arange(0, lframe), (fn1, 1)) + np.tile(np.arange(0, fn1*mframe, mframe), (lframe, 1)).T
    # 将d转换为矩阵形式（数据类型为int类型）
    d = np.array(d, dtype=np.int32)
    signal = fillsignal[d]
    return(signal, fn1, numfillzero)
lframe = int(sr*0.025)  # 帧长(持续0.025秒)
mframe = int(sr*0.001)  # 帧移
# 函数调用，把采样数组、帧长、帧移等参数传递进函数frame，并返回存储于endframe、fn1、numfillzero中
endframe, fn1, numfillzero = frame(y, lframe, mframe)

# 显示第1帧波形图
x1 = np.arange(0, lframe, 1)  # 第1帧采样点刻度
x2 = np.arange(0, lframe/sr, 1/sr)  # 第1帧时间刻度
# 显示波形图
plt.figure()
plt.plot(x1, endframe[0])
plt.xlabel('points')  # x轴
plt.ylabel('wave')  # y轴
plt.title('bluesky1 firstframe  wave', fontsize=12, color='black')
plt.show()
plt.figure()
plt.plot(x2, endframe[0])
plt.xlabel('time')  # x轴
plt.ylabel('wave')  # y轴
plt.title('bluesky1 firstframe  wave', fontsize=12, color='black')
plt.show()

运行之后首先读取音频文件，然后返回采样数组存储于y中，然后输出音频的波形图。然后进行分帧，分帧之后输出显示第一帧波形，x轴为第一帧采样点刻度：

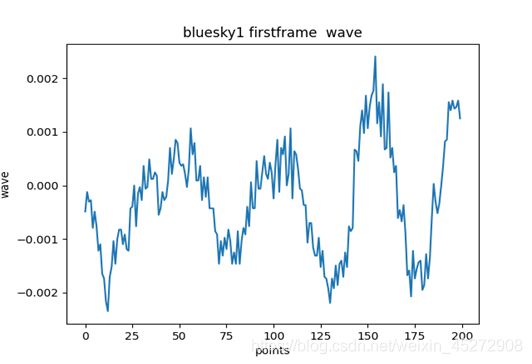
输出显示第一帧波形，x轴为第一帧时间刻度：

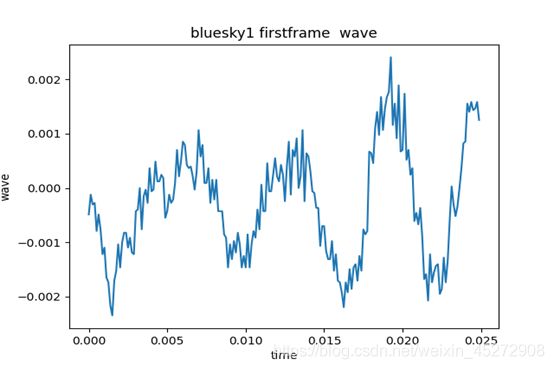
加窗

在信号分帧后，为了使帧与帧之间平滑过渡，保持连续性，也就是消除各个帧两端可能会造成的信号不连续性（即谱泄露 spectral leakage），对信号截断、分帧需要加窗，因为截断有频域能量泄露，而窗函数可以减少截断带来的影响。我们将每一帧带入窗函数，形成加窗语音信号s_w(n)=s(n)*w(n)，在语音处理中常用的为矩形窗和汉明窗。

矩形窗：
$$f(x)=\{\begin{array}{ll}1& \text{0 <=n<=L-1}\\ 0& \text{其他}\end{array}$$
汉明窗：
$$f(x)=\{\begin{array}{ll}0.54-0.46cos(2\pi n/(L-1))& \text{0 <=n<=L-1}\\ 0& \text{其他}\end{array}$$
紧接着上面的分帧后，我们继续对第一帧信号进行加窗：

'''加窗'''
import numpy as np
import librosa.display  # 导入音频及绘图显示包
import matplotlib.pyplot as plt  # 导入绘图工作的函数集合

# 读取音频文件
# 读取语音文件并绘制波形图
times = librosa.get_duration(filename='D:\任务\Bluesky1.wav')  # 获取音频时长
# 返回音频采样数组及采样率
y, sr = librosa.load('D:\任务\Bluesky1.wav', sr=8000, offset=0.0, duration=None)
# x = np.arange(0, times, 1/sr)  # 时间刻度

# 分帧
def frame(x, lframe, mframe):  # 定义分帧函数
    signal_length = len(x)  # 获取语音信号的长度
    fn = (signal_length-lframe)/mframe  # 分成fn帧
    fn1 = np.ceil(fn)  # 将帧数向上取整，如果是浮点型则加一
    fn1 = int(fn1)  # 将帧数化为整数
    # 求出添加的0的个数
    numfillzero = (fn1*mframe+lframe)-signal_length
    # 生成填充序列
    fillzeros = np.zeros(numfillzero)
    # 填充以后的信号记作fillsignal
    fillsignal = np.concatenate((x,fillzeros))  # concatenate连接两个维度相同的矩阵
    # 对所有帧的时间点进行抽取，得到fn1*lframe长度的矩阵d
    d = np.tile(np.arange(0, lframe), (fn1, 1)) + np.tile(np.arange(0, fn1*mframe, mframe), (lframe, 1)).T
    # 将d转换为矩阵形式（数据类型为int类型）
    d = np.array(d, dtype=np.int32)
    signal = fillsignal[d]
    return(signal, fn1, numfillzero)
lframe = int(sr*0.025)  # 帧长(持续0.025秒)
mframe = int(sr*0.001)  # 帧移
# 函数调用，把采样数组、帧长、帧移等参数传递进函数frame，并返回存储于endframe、fn1、numfillzero中
endframe, fn1, numfillzero = frame(y, lframe, mframe)

# 对第一帧进行加窗
hanwindow = np.hanning(lframe)  # 调用汉明窗，把参数帧长传递进去
signalwindow = endframe[0]*hanwindow  # 第一帧乘以汉明窗
x1 = np.arange(0, lframe, 1)  # 第一帧采样点刻度
x2 = np.arange(0, lframe/sr, 1/sr)  # 第一帧时间刻度
# 显示波形图
plt.figure()
plt.plot(x1, signalwindow)
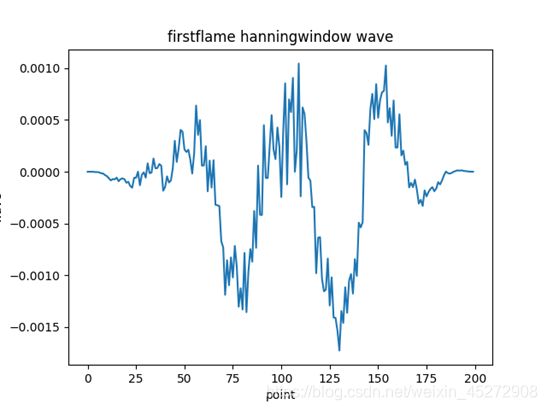
plt.xlabel('point')  # x轴
plt.ylabel('wave')  # y轴
plt.title('firstflame hanningwindow wave', fontsize=12, color='black')
plt.show()
plt.figure()
plt.plot(x2, signalwindow)
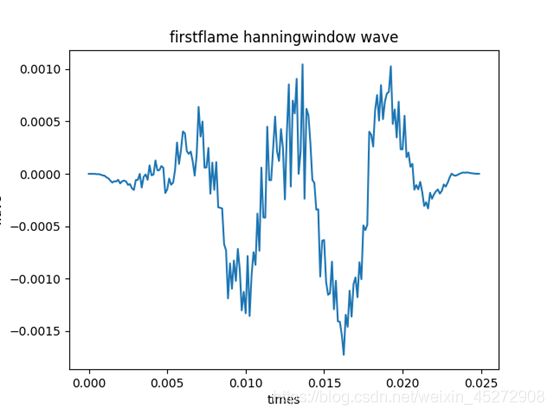
plt.xlabel('times')  # x轴
plt.ylabel('wave')  # y轴
plt.title('firstflame hanningwindow wave', fontsize=12, color='black')
plt.show()

运行之后对第一帧信号进行加窗，输出显示第一帧波形，x轴为第一帧采样点刻度：

输出显示第一帧波形，x轴为第一帧时间刻度：