MOCO论文精读-具有离散拆分送货和取货的车辆路径问题的禁忌搜索算法(Meng Qiu .et al. 2018)

Paper: A Tabu Search algorithm for the vehicle routing problem with discrete split deliveries and pickups

论文：Qiu M, Fu Z, Eglese R, et al. A Tabu Search algorithm for the vehicle routing problem with discrete split deliveries and pickups[J]. Computers & Operations Research, 2018, 100: 102-116.

被引量：70（数据来源：谷歌学术，截止到2022.03.08）

论文链接：https://doi.org/10.1016/j.cor.2018.07.021

作者介绍

Meng Qiu, Zhuo Fu,: 中南大学交通运输工程学院, 中国长沙
Richard Eglese: 兰卡斯特大学管理学院, 英国兰卡斯特
Qiong Tang: 中南大学交通运输工程学院, 中国长沙；经济与管理学院 , 衡阳师范学院，中国衡阳

本文工作

本研究对VRPDSPDP(具有离散拆分交付和取货的 VRP )的贡献有两个：

1. 描述了问题并建立了相应的数学模型，分析了VRPDSPDP的特征并给出了问题的最优解性质；
2. 开发了一种禁忌搜索算法，具有两个单独的操作，旨在避免不必要的旅行成本，加快搜索速度并增强算法搜索能力。 对所提出的启发式方法进行了测试，并将结果与​​相关文献中的结果进行了比较。

概念解释

1. 拆分装载(Splitting loads)：使某些负载由多辆车而不是一辆车运输，从而减少使用的车辆数量和行驶距离。
2. 时间窗(time windows)：顾客有服务时间的最后期限和最早开始服务时间的限制。时间窗指一个时间跨度，一个时间区间，其上下限分别为客户所能接受的最晚到达时间和所能接受的最早到达时间，因为早到和晚到都将会影响到客户的满意度，太早和太晚都有可能导致客户的不满。在物流配送系统中，时间窗是一种条件限制。软时间窗要求尽可能在时间窗内到达访问，否则将给予一定的惩罚；硬时间窗VRP则要求必须在时间窗内到达访问，否则服务被拒绝。

---

摘要

离散拆分交付(Discrete Split Deliveries and Pickups, DSPDP)和取货的车辆路径规划问题(Vehicle Routing Problem, VRP)是拆分交付和取件的车辆路径问题的变体，其中客户的需求在批次（或订单）方面是离散的。 它存在于物流配送的实践中，包括设计一组成本最低的路线来服务给定的一组客户，同时尊重车辆容量的限制。 本文对其特点进行了分析。 提出了一种数学模型和禁忌搜索算法，特别设计了批量组合和项目创建操作。 批量组合操作旨在避免不必要的旅行成本，而项目创建操作有效地加快了搜索速度，增强了算法搜索能力。 本文提供了计算结果并与文献中的其他方法进行了比较，这表明在大多数情况下，所提出的算法可以找到比文献中更好的解决方案。

---

1. Introduction

在经典的车辆路径问题（VRP）中，客户只有一个（送货或取货）需求。然而，对环境保护的日益关注导致了逆向物流的发展；除了分发给客户，回收或再制造的物品必须反向运输。为了应对这种情况，人们提出了VRP的变体，本文将其命名为VRP with Delivery and Pickups（VRPDPs）。

Parragh等人（2008年）[1]将VRPDPs分为四个子问题：

1. 具有集群回程的VRP（the VRP with Clustered Backhauls, VRPCB）；
2. 具有混合线路和回程的VRP（VRP with Mixed Linehauls and Backhauls, VRPMB）；
3. 具有同时送货和取货的VRP（VRP with Simultaneous Delivery and Pickup, VRPSDP）；
4. 具有可分送货和取货的VRP（VRP with Divisible Delivery and Pickup, VRPDDP）；
5. 具有离散拆分送货和取货的 VRP (VRP with Discrete Split Deliveries and Pickups, VRPDSPDP)

VRPCB和VRPMB中的长途和回程客户是不同的，这意味着所有客户只能有一种需求（送货或取货）。VRPCB和VRPMB之间的区别在于，前者要求在任何回程之前必须访问所有的长途运输，而后者允许长途运输和回程在行程中以任何顺序发生。与VRPCB和VRPMB相比，VRPSDP和VRPDDP中的客户可以同时有送货和取货需求。在VRPSDP中，必须满足每个客户同时满足这两个需求的限制。然而，与要求每个客户只访问一次的VRPSDP不同，在VRPDDP中，可以进行两次访问，一次送货，一次取货。

考虑到顾客为了方便可能更喜欢某一站，VRP和VRPDP总是假设每个顾客只能拜访一次，属于没有需求拆分的问题。 然而，客户的需求通过多种车辆运输的情况并不鲜见，理论研究和实际应用都证明，分担负载有利于利用车辆容量，降低车辆出行成本。 这种类型的问题被归类为具有货物分割需求的问题。 自从 Dror 和 Trudeau (1989) [2] 引入了文献中众所周知的货物可拆分交付车辆路径问题 (Split Delivery Vehicle Routing Problem, SDVRP) 以来，越来越多的学者开始研究拆分需求领域。 为了迎合 VRPDP 的拆分情况，Mitra提出了可拆分交付和取货的车辆路线问题 (Vehicle Routing Problem with Split Deliveries and Pickups, VRPSPDP)。

在关于拆分装载问题的文献中，大多数假设是连续问题，其中客户的需求可以灵活地拆分为以单元(units)（最小计量单位）为单位的任何数量的负载。这个假设有实际应用背景，但也有局限性。在实际的物流操作中，负载可能被分配给多个独立的批次或订单。一个批次或订单由多个units或仅一个unit组成，并且这被视为一个整体，不能拆分。这意味着客户的需求是离散的。例如，一个unit可以是一公斤（kg）或一立方米（$m^3$ ），具体取决于负载是按重量还是按体积计量。如果一台笔记本电脑的重量为 4 公斤，则不能将其拆分为四个部分，每个部分称一个unit，因此可以将笔记本电脑视为一个离散的批次（订单）。考虑到另一种情况，由于不同类型的货物可能需要不同的装卸设备和运输工具，因此将同一类型的货物作为一个整体分配给一个批次（订单）可更好地提高效率。本研究首次在文献中介绍了具有离散拆分送货和取货的 VRP (VRP with Discrete Split Deliveries and Pickups, VRPDSPDP)，VRPSPDP意味着每个客户可能会被一辆以上的车辆和同一辆车辆访问一次以上，尽管VRPDDP中的每个客户最多允许两次单独访问，一次用于送货，另一次用于提货，但VRPSPDP中的访问次数没有限制，VRPDSPDP又是在VRPSPDP基础上加了离散限制。

拆分负载：某些负载的交付由多辆车辆而不是一辆车辆运送，从而有机会减少使用的车辆数量和行驶距离。

具有离散拆分需求的 VRP (VRP with Discrete Split Demand, DSDVRP)：在这个问题中，每个客户需要不同批次（订单）的需求。 每批（订单）的需求可能大于一个unit，并且虽然可以多次访问客户，但每个项目必须由一辆车提供服务。VRPDDP可以归类为具有离散需求的问题的特殊情况。

2. Tabu search(禁忌搜索算法)

禁忌（Tabu Search）算法是一种元启发式(meta-heuristic)随机搜索算法，它从一个初始可行解出发，选择一系列的特定搜索方向（移动）作为试探，选择实现让特定的目标函数值变化最多的移动。为了避免陷入局部最优解，TS搜索中采用了一种灵活的“记忆”技术，对已经进行的优化过程进行记录和选择，指导下一步的搜索方向，这就是Tabu表的建立。

参考资料：

1. https://www.cnblogs.com/dengfaheng/p/9737556.html
2. https://blog.csdn.net/qq_44384577/article/details/105190912

2.1 简介

为了找到“全局最优解”，就不应该执着于某一个特定的区域。局部搜索的缺点就是太贪婪地对某一个局部区域以及其邻域搜索，导致一叶障目，不见泰山。禁忌搜索就是对于找到的一部分局部最优解，有意识地避开它（但不是完全隔绝），从而获得更多的搜索区间。兔子们找到了泰山，它们之中的一只就会留守在这里，其他的再去别的地方寻找。就这样，一大圈后，把找到的几个山峰一比较，珠穆朗玛峰脱颖而出。

1. 当兔子们再寻找的时候，一般地会有意识地避开泰山，因为他们知道，这里已经找过，并且有一只兔子在那里看着了。这就是禁忌搜索中“禁忌表（tabu list）”的含义。
2. 那只留在泰山的兔子一般不会就安家在那里了，它会在一定时间后重新回到找最高峰的大军，因为这个时候已经有了许多新的消息，泰山毕竟也有一个不错的高度，需要重新考虑，这个归队时间，在禁忌搜索里面叫做“禁忌长度（tabu length）”；
3. 如果在搜索的过程中，留守泰山的兔子还没有归队，但是找到的地方全是华北平原等比较低的地方，兔子们就不得不再次考虑选中泰山，也就是说，当一个有兔子留守的地方优越性太突出，超过了“best so far”的状态，就可以不顾及有没有兔子留守，都把这个地方考虑进来，这就叫“特赦准则（aspiration criterion）”。

这三个概念是禁忌搜索和一般搜索准则最不同的地方，算法的优化也关键在这里。

打个比方：
为了找出地球上最高的山，一群有志气的兔子们开始想办法。
1)爬山算法
兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山法，它不能保证局部最优值就是全局最优值。

2)禁忌搜索算法
兔子们知道一个兔的力量是渺小的。他们互相转告着，哪里的山已经找过，并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。

2.2 主要思路

step1：给以禁忌表H=空集，并选定一个初始解xnow；

step2：满足停止规则时，停止计算，输出结果；否则，在xnow的邻域N(xnow)中选择不受禁忌的候选集Can_N(xnow)；在Can_N(xnow)中选一个评价值最佳的解xnext，xnow=xnext；更新历史记录H，保存f(xnow)，重复step2；

step3：在保存的众多f中，挑选最小（大）值作为解；

1. 在搜索中，构造一个短期循环记忆表-禁忌表，禁忌表中存放刚刚进行过的 |T|（T称为禁忌表）个邻居的移动，这种移动即解的简单变化。
2. 禁忌表中的移动称为禁忌移动。对于进入禁忌表中的移动， 在以后的 |T|次循环内是禁止的，以避免回到原来的解，从而避免陷入循环。|T| 次循环后禁忌解除。
3. 禁忌表是一个循环表，在搜索过程中被循环的修改，使禁忌表始终保持 |T| 个移动。
4. 即使引入了禁忌表，禁忌搜索仍可能出现循环。因此，必须给定停止准则以避免出现循环。当迭代内所发现的最好解无法改进或无法离开它时，算法停止。

2.3 注意事项

• 禁忌对象：可以选取当前的值（cur）作为禁忌对象放进tabu list，也可以把和当前值在同一“等高线”上的都放进tabu list。
• 为了降低计算量，禁忌长度和禁忌表的集合不宜太大，但是禁忌长度太小容易循环搜索，禁忌表太大容易陷入“局部极优解”。
• 对best_so_far的操作是直接赋值为最优的“解禁候选解”，但是有时候会出现没有大于best_so_far的，候选解也全部被禁的“死锁”状态，这个时候，就应该对候选解中最佳的进行解禁，以能够继续下去。
• 终止准则：和模拟退火，遗传算法差不多，常用的有：给定一个迭代步数；设定与估计的最优解的距离小于某个范围时，就终止搜索；当与最优解的距离连续若干步保持不变时，终止搜索；
• 邻域：系统总是在初始点的邻域搜索可能解的,因而必须定义适合的邻域空间,如果解空间存在一个最优解X*,初始搜索点为S0,那么如果S0不存在到达X*的通路,就会使搜索陷入S0的邻域的局部最优解。可以证明如果邻域满足对称性条件，则在假设禁忌表足够长的情况下必然可搜索到全局最优解。

2.4 相关概念解释

1. 邻域
   官方一点：所谓邻域，简单的说即是给定点附近其他点的集合。在距离空间中，邻域一般被定义为以给定点为圆心的一个圆；而在组合优化问题中，邻域一般定义为由给定转化规则对给定的问题域上每结点进行转化所得到的问题域上结点的集合。
   通俗一点：邻域就是指对当前解进行一个操作(这个操作可以称之为邻域动作)可以得到的所有解的集合。那么邻域的本质区别就在于邻域动作的不同了。

2. 邻域动作
   邻域动作是一个函数，通过这个函数，对当前解s，产生其相应的邻居解集合。例如：对于一个bool型问题，其当前解为：s = 1001，当将邻域动作定义为翻转其中一个bit时，得到的邻居解的集合N(s)={0001,1101,1011,1000}，其中N(s) ∈ S。同理，当将邻域动作定义为互换相邻bit时，得到的邻居解的集合N(s)={0101,1001,1010}。

3. 禁忌表
   包括禁忌对象和禁忌长度。（当兔子们再寻找的时候，一般地会有意识地避开泰山，因为他们知道，这里已经找过，并且有一只兔子在那里看着了。这就是禁忌搜索中“禁忌表（tabu list）”的含义，兔子呆着的时间成为禁忌长度。）

4. 侯选集合
   侯选集合由邻域中的邻居组成。常规的方法是从邻域中选择若干个目标值或评价值最佳的邻居入选。

5. 禁忌对象
   禁忌算法中，由于我们要避免一些操作的重复进行，就要将一些元素放到禁忌表中以禁止对这些元素进行操作，这些元素就是我们指的禁忌对象。（当兔子们再寻找的时候，一般地会有意识地避开泰山，因为这里找过了。并且还有一只兔子在这留守。）

6. 禁忌长度
   禁忌长度是被禁对象不允许选取的迭代次数。一般是给被禁对象x一个数（禁忌长度） t ，要求对象x 在t 步迭代内被禁，在禁忌表中采用tabu(x)=t记忆，每迭代一步，该项指标做运算tabu(x)=t−1，直到tabu(x)=0时解禁。于是，我们可将所有元素分成两类，被禁元素和自由元素。禁忌长度t 的选取可以有多种方法，例如t=常数，或t=[√n]，其中n为邻域中邻居的个数；这种规则容易在算法中实现。
   （那只留在泰山的兔子一般不会就安家在那里了，它会在一定时间后重新回到找最高峰的大军，因为这个时候已经有了许多新的消息，泰山毕竟也有一个不错的高度，需要重新考虑，这个归队时间，在禁忌搜索里面叫做“禁忌长度（tabu length）”。）

7. 评价函数
   评价函数是侯选集合元素选取的一个评价公式，侯选集合的元素通过评价函数值来选取。以目标函数作为评价函数是比较容易理解的。目标值是一个非常直观的指标，但有时为了方便或易于计算，会采用其他函数来取代目标函数。

8. 特赦规则
   在禁忌搜索算法的迭代过程中，会出现侯选集中的全部对象都被禁忌，或有一对象被禁，但若解禁则其目标值将有非常大的下降情况。在这样的情况下，为了达到全局最优，我们会让一些禁忌对象重新可选。这种方法称为特赦，相应的规则称为特赦规则。
   （如果在搜索的过程中，留守泰山的兔子还没有归队，但是找到的地方全是华北平原等比较低的地方，兔子们就不得不再次考虑选中泰山，也就是说，当一个有兔子留守的地方优越性太突出，超过了“best so far”的状态，就可以不顾及有没有兔子留守，都把这个地方考虑进来，这就叫“特赦准则（aspiration criterion）”。）

2.5 其他类似算法

• 模拟退火算法是源于对热力学中退火过程的模拟，在某一给定初温下，通过缓慢下降温度参数，使算法能够在多项式时间内给出一个近似最优解。退火与冶金学上的‘退火’相似，而与冶金学的淬火有很大区别，前者是温度缓慢下降，后者是温度迅速下降。
• 遗传算法是基于生物进化的原理发展起来的一种广为应用的、高效的随机搜索与优化的方法。其主要特点是群体搜索策略和群体中个体之间的信息交换，搜索不依赖于梯度信息。
• 蚁群算法是群体智能可用于解决其他组合优化问题,比如有n个城市，需要对所有n个城市进行访问且只访问一次的最短距离。

3. Problem description and properties

VRPDSPDP旨在设计最优路线集，以最低的成本（最少的车辆和最短的行程距离）满足所有客户的需求，同时满足以下约束：

1. 所有车辆在同一仓库(Depot)发回；
2. 所有车辆均质(homogeneous)，不允许超载；
3. 客户可能有送货和取货需求，其中任何一个都可能超过车辆容量；
4. 每位客户可乘坐多种车辆或一辆车多次访问；
5. 线路和回程可以沿车辆路线以任意顺序发生；
6. 没有时间窗口或最大路线长度的限制。

一般来说，拥有或租用一辆车相关的固定成本远大于通过以使用更多车辆为代价缩短行程距离所节省的成本。 因此，我们将最小车辆数量设置为输入参数。

令 $G=(V,E)$ 是给定的无向网络，其中 $V=0\cup N$是顶点集（顶点 i = 1，…，n 对应于客户，而顶点 0 对应于仓库）和 $E=(i,j)|i,j\in V,i=j$是边集。 每条边$ (i, j) ∈ E $对应一个非负 $c_{ij}$ ，表示从顶点 i 到顶点 j 的成本。 最大车辆容量为$Q$ ，使用的车辆数量为 $K$ 。我们将 $D{M}_i$ 和 $P{M}_i$ 设置为客户$i$ 的交货批次和取货批次数。$d_i^m(m=1,...,D{M}_i)$为客户 $i$ 第 $m$ 批交货的需求负荷.$D_i={\sum }_{m=1}^{D{M}_i}{d}_i^m$为客户$i$的交货总量，同理，$p_i$和$P_i={\sum }_{m=1}^{P{M}_i}{p}_i^m$为取货的批处理需求以及取货的总和。

在此基础上所修改的VRPDSPDP公式：

• 公式(1) 目标是最小化车辆行驶的总距离；
• 公式(2) 每位顾客至少服务一次；
• 公式(3) - (4) 车辆出库并返回库；
• 公式(4)车辆访问客户后离开；
• 公式(5) – (7) 满足每个客户的需求；
• 公式(6) 最大容量约束；
• 公式(7) – (11) 设置 $x_{ij}^k,y_{im}^k,z_{im}^k$为 0 –1。

3.1 Problem properties

客户的每一批次（订单）都是一个绝对的对象，相互独立。 由于坐标位置相同，同一客户的一对批次（a pair of batches, 交付和/或取货？）之间的距离为零。 在讨论 VRPDSPDP 的属性之前，先解释一下路径的表达式。 如上节所述，客户 i 的交货和取货需求分别由 DM i 和 PM i 批次（订单）组成。 因此，一条路径被表示为一个序列，该序列由代表仓库或访问客户的顶点编号以及在该访问时处理的批次（交付和/或取货）的需求组成。如：
$$0-6\left(d_6^9,p_6^5\right)-8\left(0,p_8^1+p_8^8\right)-0$$
解释：车辆从仓库出发，首先拜访客户 6，卸下第九批交货（订单）并收集第五批提货，分别命名为$d_6^9$和$p_6^5$ 。 离开客户6后，车辆前往拜访客户8。由于客户8的交付负载量为零，因此车辆在客户8处没有送货计划。但车辆运送第一批和第八批提货，客户 8 回到仓库。

为了研究 VRPSPDP 的特性，我们讨论图 1 所示的示例，网络中有 3 个客户（括号中的数字代表交付和取货批次的总需求，以逗号分隔）。 每条边旁边的数字表示对应的代价（距离），代价矩阵满足三角不等式(两边之和大于第三边)。 车辆容量为 10，因此所需的最小车辆数量为 2。

虽然 VRPSPDP 中的需求是连续的，并且可以以任何方式拆分以适应车辆的可用容量，但 VRPDSPDP 中的需求是离散的，不能像 VRPSPDP 中那样任意拆分。 明确客户交付和取货值对于这两个问题的比较。 我们假设 VRPDSPDP 中的需求按单元拆分，如图 2 所示，

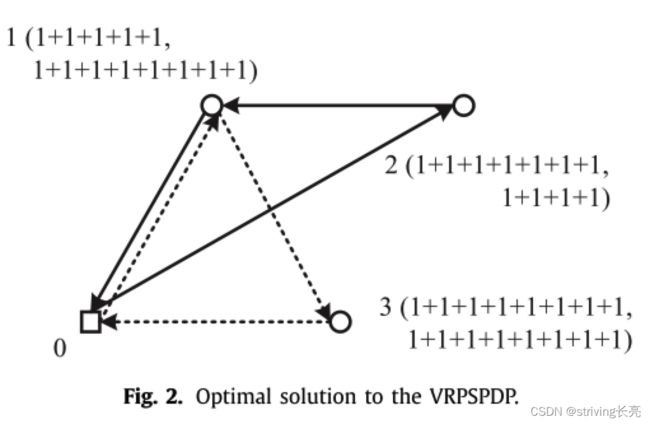
VRPDSPDP 中的需求拆分为几个独立的批次，如图 3 所示。

最佳解决方案的路径显示在相应的问题说明下方。 粗体数字为分割点，每点旁边括号内的两个数字用逗号隔开，分别表示发货量和取货量。 在给定 VRPDSPDP 的上述解决方案中，三个点被拆分，比 VRPSPDP（两个拆分点）中的要多。 此外，VRPSPDP 的总距离 ( 10 + 2 √ 3 = 13 . 46 ) 比 VRPDSPDP (18.93) 短。 事实上，无论是货物分割点数还是目标总距离值，VRPSPDP都比VRPDSPDP要小。

4. A Tabu Search algorithm for the VRPDSPDP

TS 是一种基于记忆的搜索策略，用于指导局部搜索方法在局部最优之外继续搜索。 实现此目的的一种方法是在禁忌列表中跟踪过去所做的最近移动或解决方案的属性。 每当算法试图在禁忌列表中移动时，该移动就会被禁止。

4.1 Initial solution

禁忌搜索算法对初始解有一定的依赖性。 一个好的初始解可以帮助 TS 在解空间中找到一个好的最终解，而一个较差的初始解会降低 TS 的收敛速度。 一般来说，在解决特定问题时，可以使用其他算法生成高质量的初始解，然后使用 TS 进一步提高解的质量。 设计良好的 TS 的解决方案不应强烈依赖于初始解决方案的质量，如果 TS 使用并发操作，那么从不同的初始解决方案获得的多样性可能会有一些优势。 因此，找到随机生成的初始解的情况并不少见。

在本文中，客户的每个批次（订单）在开始时都是一个绝对对象(absolute object)，作为一个单独的项目。也就是说，存在$D{M}_i+P{M}_i$同一地点(co-located)的虚拟客户。由于问题的严重复杂性，TS的运行时间要求尽可能短，这初始解的质量更重要，我们更喜欢随机生成初始解，过程耗时更少，并为TS留下更多进一步提高解质量的机会。因此，初始解决方案是通过建立连续路线生成的，在这些路线上随机选择下一个item，并将其添加到路线的末端，除非这违反了容量限制约束，在这种情况下，返回车辆段的路线完成，新路线开始。初始解决方案中使用的车辆路线数可能超过所需的最小值，但禁忌搜索的目的是尽可能减少车辆路线数。

4.2 Batch combination

由于每个离散的批次（订单）被视为一个独立的对象，因此存在同一客户在一次行程中被多次拜访的情况。以图 4 为例，顶点 i 和 j 对应于同一客户的两个不同batch。

在同一条路线上拜访客户两次（batch i 一次，batch j 一次），与拜访客户一次相比，通常会增加路线距离。 为了避免这种情况，我们设计了一种特殊操作，将同一客户的批次移动到一次访问中，这样做是可行的，方法是将顶点 j 分配到顶点 i 旁边。 如图 4 所示，除了将顶点 j 移到顶点 i 后面之外，将 j 重新定位到 i 前面（→ a → j → i → b → ）或将 i 放在 j 旁边（→ c → i → j → d → or → c → j → i → d → ) 可能会得到不同的结果。 为避免以相同的成本探索多种解决方案并合理缩短运行时间，我们只考虑图4所示的运动。 此举是VRPDSPDP路径改进的基础算子，为进一步的邻域结构奠定了基础。

4.3 Item creation

原因：在传统的邻域搜索中，有一个基本假设，即移动对象是单个客户。 但是，VRPDSPDP的操作对象实际上是每个batch（订单）； 因此，仅使用路径中的batch都包含在内的客户并不能反映离散拆分的特征。 但是，将单个批次作为操作对象会导致计算密集且耗时的过程，因为批次的数量远远大于客户的数量。

考虑到上述情况，本文设计了一个个体算子(individual operator)，旨在创建一个邻域移动对象，它对应于本文中的一个“item”。

1. 项目创建操作首先从选定的路径中随机选择一个订单顶点;
2. 然后向前和向后搜索以检查是否存在具有相同客户来源的其他订单。
3. 之后，随机选择代表单次访问中处理的客户订单的路径中的一个或多个相邻顶点以创建item。 通过设计操作创建的项目由路线上的一个、几个或所有批次的客户组成。

如图5所示，选取的订单顶点是i（步骤1），通过前后检查，t、i、j和k显示为与同一客户相关(步骤2)。 假设 i、j 和 k 是选择的相邻批次顶点以创建表示为顶点 $i\ast$ 的item。

在本文的其余部分，为了简洁起见，我们将路线路径(route path)的每个顶点称为一个item，如$i\ast$。

operator考虑了一个客户的所有需求，包括 t、i、j 和 k，在一次访问中提供服务。 如上图所示，假设 t 表示发货订单(batch)，i、j 和 k 是取货订单，则 Item Creation 将客户拆分为送货商品（t）和取货商品（i、j 和 k）。

4.4 Neighbourhood structure

局部搜索方法(Local search methods)已被证明可以有效地解决 VRPSDP。 局部搜索方法中的几个常用的为 2-opt、2-opt∗、3-opt、or-opt、swap、shift、reverse、cross、relocate 和 relocate split，它们用于找到 VRPSPDP 或 VRPDDP 的解决方案。关于此类算法具体介绍，本文不多涉及，感兴趣的可以百度哈~

这里我们就举一个2-opt算法最原始应用的例子——解决TSP问题：

假设有一个旅行商必须要从A城市出发经过BCDEFGH这几个城市最后回到A城市(可以理解为约束条件)，目标函数是路程最短(更广义的说是 费用最少)。

首先我们可以任选一个可行解s={A,B,C,D,E,F,G,H,A}，并假设s是最优解Smin。然后使用2-opt算法进行问题的求解：随机选取两点i和k，将i之前的路径不变添加到新路径中，将i到k之间的路径翻转其编号后添加到新路径中，将k之后的路径不变添加到新路径中。

原路径: A --> B --> C --> D --> E --> F -->G --> H --> A
i = 4, k =7

新路径:

1. (A --> B -->C)
2. A -->B -->C–> (G --> F --> E --> D)
3. A --> B --> C–> G --> F --> E --> D (–> H --> A)

从而获得一个新的可行解。将可行解代入目标函数可得目标函数值，将其与Smin的目标函数值比较，取两者目标函数值较小的可行解为Smin，直到找不到比Smin还小的函数值为止。至此，该TSP问题已用2-opt算法解决。

很容易将2-opt算法推广到k-opt算法，即将上例s中的k个元素进行调换，以更换可行解并检验其在目标函数中的优度。2-opt也叫2-exchange方法。或者说k-exchange，其中k≥2 。

除了 Relocate 算子和 Relocate split 算子专门针对拆分负载而设计外，大部分局部搜索方法都考虑了客户的移动，无论其需求是否被拆分。

在我们的启发式中，由于item创建的操作，对于这些移动的操作，客户与要交付或取货的item之间的差异可以忽略不计。 在我们的实现中，五个类的邻域移动被应用于当前的解决方案。 这些移动包括两个路线内的操作和三个不同路线之间的操作。 表 5 提供了简要介绍。

本节的其余部分提供了上述动作的详细说明。

• (路线内的操作)对于intra-swap和intra-reverse，从当前解决方案中随机选择一个route，然后为该route创建并选择两个不同客户的item。

• (不同路线之间的操作)关于inter move、inter-reassignment、inter-swap和tail-swap，随机选择两条不同的路径，每条路径生成一个item。

• Intra-swap
  在此移动中，两个不同客户的item(i和j)位置被交换，并生成一个新的路线，如图6所示。
  

• Intra-reverse
  此移动中的每个item都是一个以 i 开头并以 j 结尾的子路径。 Intra-reverse 的邻域移动将子路径中所有批次的顺序反转并产生新的route，是item内部的顺序变化,如图 7 所示。
  

• Inter-reassignment
  假设随机选择的路线是路线1和路线2。以图8所示的示例为例，我们从路线1中删除item $i$，并在此移动中将其分配给路线2。
  图 9 说明了一种特殊情况：Route 1 上只有一个客户，因此，将 i 移动到 Route 2 后，Route 1 中不存在顶点。针对这种情况，我们设计了一个名为消除的操作。 如果当前解决方案中使用的车辆数量超过所需的最小值时，会实施消除并生成新的解决方案，从而节省一辆车。
  

• Inter-swap
  在这个移动中，item i和j的位置被交换(和上一个不同之处在于，swap并没有删除操作)，并且获得了两条新路径，如图10所示。
  

• Tail-swap
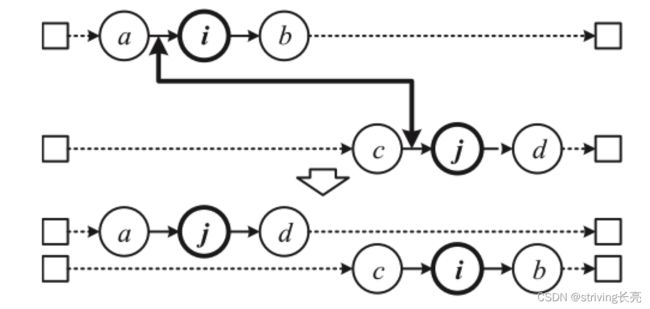
  换尾操作如图11所示； Route 1 中的 tail ( i → b → ) 和 Route 2 中的 tail ( j → d → ) 交换，生成两条新路由。 这种邻里结构允许在车辆容量方面采取不可行的解决方案。 这种结构能够增强 TS 算法。
  

4.5 Evaluation of the solutions

VRPDSPDP 有两个需要优化的目标：总行驶成本（距离）和固定成本（使用的车辆数量）。

如关于 VRPDSPDP 所述，优先考虑固定成本。 因此，具有一定数量车辆的可行解决方案总是优于任何其他需要更多车辆的可行解决方案。 对于车辆数​​量相同的解决方案，选择总出行成本最低的解决方案。

为了便于搜索空间的探索，本文允许item的移动，即使它会导致不可行的解决方案。不可行的程度可以通过在目标函数中加入车辆通行能力来衡量，如果约束条件被打破，可以增加惩罚，引入了惩罚，产生了可行和不可行的混合解决方案，并避免了在VRP的禁忌路由算法中陷入局部极小值的可能性。我们采用该机制，并使用以下公式：
$$\sum _{k=1}^K[E(r)+p\cdot A(r)]$$
其中，
$K$ 是解决方案中的路线总数，$E(r)$ 是路线 $r$ 的行驶成本，$A(r)$ 是沿路线 $r$ 的多余边数，$p$ 是惩罚系数。
如果解决方案可行，则 $A(r)$ 对于所有路径都为零。
$p\in [0.000001,200000]$ 在开始时等于 1，并自己调整权重：每 10 次迭代，如果所有 10 个先前的解决方案都可行，则除以 2 ,如果它们都是不可行的,那么就乘以 2 。

4.6 Tabu list

我们为不同类别的移动创建了五个独立的禁忌列表。每个禁忌列表都包含最近五到八次 (随机选择) 迭代中解决方案的移动属性。对于禁忌状态的记录，可以构造一组$n\times n$矩阵。

例如，如果为内部交换移动选择了顶点i和j，则禁忌状态将保存在intra-wap矩阵的元素 (i，j) 中。在每次迭代中，将执行的最后一次移动的禁忌状态添加到列表中，而其他动作则减少一，直到它们等于零。

4.7 TS algorithm

TS算法描述中使用的变量及其解释:

• Iter :当前迭代轮数
• ConsIter: 当前的连续迭代次数，到目前为止没有对最佳解决方案进行任何改进。
• MaxConsIter: 迄今为止，对最佳解决方案没有任何改进的最大连续迭代次数。
• CandList: 列表中当前候选移动的数量。
• MaxCandList: 列表中候选移动的最大数量。

启发式的伪代码如下：

1. 初始化
2. 输入数据和参数；
3. 随机生成一个初始可行解，并将其设置为当前解和目前为止的最佳解；
4. 构建五个独立的邻域搜索禁忌列表；
5. While (ConsIter < MaxConsIter) do begin
6. While (CandList < MaxCandList) do begin
7. 随机选择五种邻域移动中的一种，创建对应的项；
8. 对当前解进行相应的操作；
9. 如果满足淘汰条件，则执行淘汰，移除一条路线（有疑问，淘汰是路线不合规范还是最差的呢？）。
10. 进行批量组合，生成新的候选解；
11. 将所选移动产生的解决方案添加到候选列表中；
12. 结束；
13. 如果没有被禁忌或者比目前最好的解决方案更好的解决方案，则在候选列表中选择最佳解决方案（特赦规则）；
14. 将新解设置为当前解，更新禁忌列表，增加Iter；
15. 如果新解决方案改进了目前为止的最佳解决方案，则更新目前为止的最佳解决方案并将ConsIter设置为0； 否则，增加 ConsIter；
16. 更新对应的禁忌列表；
17. 结束。

5. Computational results and comparisons

5.1 A priori split strategy

据我们所知，目前的研究没有为 VRPDSPDP 设计的任何测试基准，也没有任何拆分策略来为相应的 VRPDSPDP 生成离散需求。 曾经有人提出了两种先验拆分策略，在 SDVRP 中而不是在算法过程中提前拆分交付，旨在将每个客户的需求拆分为多个商品部分（离散批次或订单），以便充分利用 车辆的容量。

本文提出了两种类似的拆分策略，命名为 20/10/5/1/ x 和 25/10/5/1/ x ，以适应 VRPSPDP 中的离散需求。 以 20/10/5/1/ x 为例，我们假设每个客户的需求只能被拆分并分配到五个单独的组中，每个组的数量都不同。 四组批次的固定需求(车辆需求)分别为 0.2Q 、 0.1Q 、 0.05Q 和 0.01Q 。 第五组包括数量小于 0.01Q 的负载。$D_i$ ，也就是给客户 i 的订单货物，将分为五个不同的组 $W_s(s=20,10,5,1,x)$。 $W_s$中的每个批次的需求量为 $T_s$ ，属于 $W_s$的订单数记为 $H_s$ 。 20/10/5/1/x的策略如表7所示（$\lfloor u\rfloor$为不大于u的最大整数）。

本文还提出了 25/10/5/1/ x 策略，其基本原理与 20/10/5/1/ x 相同。 例如，如果 Q = 1000 且 $D_i$= 566，则通过 20/10/5/1/ x 策略将$D_i$需求分为 200、200、100、50、10 和 6 ，采用 25/10/5/1/ x 策略则分为 250， 250、50、10 和 6 。 我们在计算实验中使用这两种策略。

具体计算（我个人理解）：第五组包括数量小于 0.01Q 的负载，所以 20/10/5/1/ x 应为200,100,50,10，还剩下206，x不能大于0.01Q，所以要再分一次200，剩下6；同理，25/10/5/1/ x 应为250,100,50,10，余下566-410=156，不管是多分一次100还是50都不符合，所以为保证分的组数尽可能少，所以多分一次250，去掉100，最终为250， 250、50、10 和 6

5.2 Performance of the a priori split strategy

我们将具有 20/10/5/1/ x 和 25/10/5/1/ x 拆分策略的 TS 算法应用于不同类别的 VRPSPDP 实例，在我们的TS算法中，我们将变量MaxConsIter和MaxCandList分别设置为$4500+10\ast n$和$150+2\ast n$。

每种策略下每个客户交付和提货的离散批次：

本文采用了多种公开数据集，分别是Mitra(2008)[3]、Yin(2013)[4]

为了显示解决方案的性能，进行了比较，包括相应的路线、沿途客户的送货和取货负载以及总路线距离。

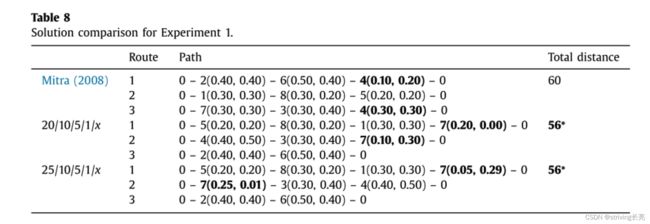
1. 实验1：与Mitra相比，本文的distance都是56，这比Mitra[3]的解决方案要好，距离缩短了6.67%。如表8所示，在我们的解决方案中，将客户7分为两条路线，并没有将客户4的订单split。

2. 实验2：策略20/10/5/1/ x (308.74) 减少了Yin et al. (320.11) 的总距离3.55%。25/10/5/1/ x (311.87) 的解也优于Yin的解。

使用解的波动系数来评估所得解的质量(solution quality)，其计算公式如下：
$$\text{ fluctuation coefficient }=\frac{\max \text{ value }-\text{ min value }}{\text{ average value }}\times 100\%$$

在与Yin的对比中，TS算法的收敛性和解的质量都显示出了优秀的表现，通过对收敛性和解质量的分析，该算法表明收敛性好，解质量稳定，在此就不附图了。

实验 1 和 2 展示了我们启发式算法的良好性能。 为了进一步确认我们的 TS 算法的有效计算能力，本实验测试了更多实例（Mitra (2005) 为 VRPSPDP 给出的三组问题）。 每对客户之间的距离有两种情况(交货以及取货),对于这两种情况，路线成本是对称的。 具体分析可以查看原文。

5.3 Performance on the DSDVRP

为了更好地判断算法的质量，本文对DSDVRP进行了另一组计算实验比较。本实验使用了Chen等人(2017)[5]提供的数据。表14和表15给出了解决方案比较，所有实例解决方案均采用我们的TS算法，以最少的车辆数量进行求解。具体参照原文。

总结

VRPDSPDP不仅在理论上很有意义，而且在配送中也有实际应用。允许多个车辆访问客户，通过充分利用车辆容量并减少路线距离可节省差旅成本。在这项工作中，我们描述了这个问题，并建立了相应的数学模型，分析了VRPDSPDP的特点，给出了问题的最优解性质，提出了一种禁忌搜索算法，设计了两个独立的运算，避免了不必要的旅行费用，加快了搜索速度，增强了算法的搜索能力。计算结果表明，在大多数情况下，所提出的TS算法可用于找到比文献中更好的解决方案，以解决约束较小的VRPSPDP。

在未来的研究中，包括开发VRPDSPDP的特殊结构，这可能会进一步改善所提出方法的性能。未来的研究还可能包括额外的离散需求限制对解决方案成本的影响。我们认为，值得进一步探索新的 “Item Creation”，以关注由于其不同的替代最优方案而导致的所提出公式的局限性，这能够减少可以考虑的替代方案的数量。

---

References

1. Parragh S N, Doerner K F, Hartl R F. A survey on pickup and delivery problems[J]. Journal für Betriebswirtschaft, 2008, 58(1): 21-51.
2. Dror M, Trudeau P. Savings by split delivery routing[J]. Transportation Science, 1989, 23(2): 141-145.
3. Mitra, S. , 2008. A parallel clustering technique for the vehicle routing problem with split deliveries and pickups. J. Oper. Res. Soc. 59 (11), 1532–1546
4. Yin, C. , Bu, L. , Gong, H. , 2013. Mathematical model and algorithm of split load vehicle routing problem with simultaneous delivery and pickup. Int. J. Innov. Comput. I. 9 (11), 4497–4508
5. Chen, P. , Golden, B. , Wang, X. , Wasil, E. , 2017. A novel approach to solve the split delivery vehicle routing problem. Int. T. Oper. Res. 24 (1-2), 27–41 .