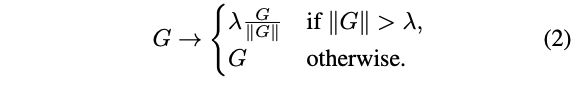NFNet：NF-ResNet的延伸，不用BN的4096超大batch size训练 | 21年论文

论文认为Batch Normalization并不是网络的必要构造，反而会带来不少问题，于是开始研究Normalizer-Free网络，希望既有相当的性能也能支持大规模训练。论文提出ACG梯度裁剪方法来辅助训练，能有效防止梯度爆炸，另外还基于NF-ResNet的思想将SE-ResNet改造成NFNet系列，可以使用4096的超大batch size进行训练，性能超越了Efficient系列

来源：晓飞的算法工程笔记 公众号

论文: High-Performance Large-Scale Image Recognition Without Normalization

• 论文地址：https://arxiv.org/abs/2102.06171
• 论文代码：https://github.com/deepmind/deepmind-research/tree/master/nfnets

Introduction

---

  目前，计算机视觉的大部分模型都得益于深度残差网络和batch normalization，这两大创新能够帮助训练更深的网络，在训练集和测试集上达到很高的准确率。特别是batch normalization，不仅能够平滑损失曲线，使用更大的学习率和batch size进行训练，还有正则化的作用。然而，batch normalization并不是完美，batch normalization在实践中有三个缺点：

• 计算消耗大，内存消耗多。
• 在训练和推理上的用法不一致，并且带来额外的超参数。
• 打破了训练集的minibatch的独立性。

  其中，第三个问题最为严重，这会引发一系列的负面问题。首先，batch normalization使得模型难以在不同的设备上复现精度，而且分布式训练经常出问题。其次，batch normalization不能用于要求每轮训练样本独立的任务中，如GAN和NLP任务。最后，batch normalization对batch size十分敏感，在batch size较低时表现较差，限制了有限设备上的模型大小。
  因此，尽管batch normalization有很强大的作用，部分研究者仍在寻找一种简单的替代方案，不仅需要精度相当，还要能用在广泛的任务中。目前，大多数的替代方案都着力于抑制残差分支的权值大小，比如在残差分支的末尾引入一个初始为零的可学习的标量。但这些方法不是精度不够，就是无法用于大规模训练，精度始终不如EfficientNets。
  至此，论文主要基于之前替代batch normalization的工作，尝试解决其中的核心问题，论文的主要贡献如下：

• 提出Adaptive Gradient Clipping(AGC)，以维度为单位，基于权值范数和梯度范数的比例进行梯度裁剪。将AGC用于训练Normalizer-Free网络，使用更大batch size和更强数据增强进行训练。
• 设计Normalizer-Free ResNets系列，命名为NFNets，在ImageNet上达到SOTA，其中NFNet-F1与EfficientNet-B7精度相当，训练速度快8.7倍，最大的NFNet可达到86.5%top-1准确率。
• 实验证明，在3亿标签的私有数据集上预训练后，再在ImageNet上进行finetune，准确率能比batch normalization网络要高，最好的模型达到89.2%top-1准确率。

Understanding Batch Normalization

---

  论文探讨了batch normalization的几个优点，这里简单说一下：

• downscale the residual branch：batch normalization限制了残差分支的权值大小，使得信号偏向skip path直接传输，有助于训练超深的网络。
• eliminate mean-shift：激活函数是非对称且均值非零的，使得训练初期激活后的特征值会变大且均为正数，batch normalization恰好可以消除这一问题。
• regularizing effect：由于batch normalization训练时用的是minibatch统计信息，相当于为当前batch引入了噪声，起到正则化的作用，可以防止过拟合，提高准确率。
• allows efficient large-batch training：batch normalization能够平滑loss曲线，可以使用更大的学习率和bach size进行训练。

Towards Removing Batch Normalization

---

  这篇论文的研究基于作者之前的Normalizer-Free ResNets(NF-ResNets)进行拓展，NF-ResNets在去掉normalization层后依然可以有相当不错的训练和测试准确率。NF-ResNets的核心是采用$h_{i+1}=h_i+\alpha f_i(h_i/{\beta }_i)$形式的residual block，$h_i$为第$i$个残差块的输入，$f_i$为第$i$个residual block的残差分支。$f_i$要进行特殊初始化，使其有保持方差不变的功能，即$Var(f_i(z))=Var(z)$。$\alpha =0.2$用于控制方差变化幅度，${\beta }_i=\sqrt{Var(h_i)}$为$h_i$的标准差。经过NF-ResNet的residual block处理后，输出的方差变为$Var(h_{i+1})=Var(h_i)+{\alpha }^2$。
  此外，NF-ResNet的另一个核心是Scaled Weight Standardization，用于解决激活层带来的mean-shift现象，对卷积层进行如下权值重新初始化：

  其中，${\mu }_i=(1/B){\sum }_j{W}_{ij}$和${\sigma }_i^2=(1/N){\sum }_j(W_{ij}-{\mu }_i{)}^2$为对应卷积核的某行(fan-in)的均值和方差。另外，非线性激活函数的输出需要乘以一个特定的标量$\gamma$，两者配合确保方差不变。
  之前发布的文章也有NF-ResNet的详细解读，有兴趣的可以去看看。

Adaptive Gradient Clipping for Efficient Large-Batch Training

---

  梯度裁剪能够帮助训练使用更大的学习率，还能够加速收敛，特别是在损失曲线不理想或使用大batch size训练的场景下。因此，论文认为梯度裁剪能帮助NF-ResNet适应大batch size训练场景。对于梯度向量$G=\partial L/\partial \theta$，标准的梯度裁剪为：

  裁剪阈值$\lambda$是需要调试的超参数。根据经验，虽然梯度裁剪可以帮助训练使用更大的batch size，但模型的效果对阈值$\lambda$的设定十分敏感，需要根据不同的模型深度、batch size和学习率进行细致的调试。于是，论文提出了更方便的Adaptive Gradient Clipping(AGC)。
  定义$W^l\in {\mathbb{R}}^{N\times M}$和$G^l\in {\mathbb{R}}^{N\times M}$为$l$层的权值矩阵和梯度矩阵，$\Vert \cdot {\Vert }_F$为F-范数，ACG算法通过梯度范数与权值范数之间比值$\frac{\Vert G^l{\Vert }_F}{\Vert W^l{\Vert }_F}$来进行动态的梯度裁剪。在实践时，论文发现按卷积核逐行(unit-wise)进行梯度裁剪的效果比整个卷积核进行梯度裁剪要好，最终ACG算法为：

  裁剪阈值$\lambda$为超参数，设定$\Vert W_i{\Vert }_F^{\ast }=max(\Vert W_i{\Vert }_F,ϵ=10^{-3})$，避免零初始化时，参数总是将梯度裁为零。借助AGC算法，NF-ResNets可以使用更大的batch size(4096)进行训练，也可以使用更复杂的数据增强。最优的$\lambda$需考虑优化器、学习率和batch size，通过实践发现，越大的batch size应该使用越小的$\lambda$，比如batch size=4096使用$\lambda =0.01$。
  ACG算法跟优化器归一化有点类似，比如LARS。LARS将权值更新值的范数固定为权值范数的比值$\Delta w=\gamma \ast \eta \ast \frac{\Vert w^l\Vert }{\Vert \nabla L(w^l)\Vert }\ast \nabla L(w_t^l)$，从而忽略梯度的量级，只保留梯度方向，能够缓解梯度爆炸和梯度消失的现象。ACG算法可以认为是优化器归一化的松弛版本，基于权值范数约束最大梯度，但不会约束梯度的下限或忽略梯度量级。论文也尝试了ACG和LARS一起使用，发现性能反而下降了。

Normalizer-Free Architectures with Improved Accuracy and Training Speed

  论文以带GELU激活的SE-ResNeXt-D模型作为Normalizer-Free网络的基础，除训练加入ACG外，主要进行了以下改进：

• 将$3\times 3$卷积变为分组卷积，每组的维度固定为128，组数由卷积的输入维度决定。更小的分组维度可以降低理论的计算量，但计算密度的降低导致不能很好地利用设备稠密计算的优势，实际不会带来更多加速。
• ResNet的深度扩展(从resnNet50扩展至ResNet200)主要集中在stage2和stage3，而stage1和stage4保持3个block的形式。这样的做法不是最优的，因为不管低层特征或高层特征，都需要足够的空间去学习。因此，论文先制定最小的F0网络的各stage的block数为$[1,2,6,3]$，后续更大网络都在此基础上以倍数扩展。
• ResNet的各stage维度为$[256,512,1024,2048]$，经过测试之后，改为$[256,512,1536,1536]$，stage3采用更大的容量，因为其足够深，需要更大的容量去收集特征，而stage4不增加深度主要是为了保持训练速度。

• 将NF-ResNet的bottleneck residual block应用到SE-ResNeXt中并进行修改，在原有的基础上添加了一个$3\times 3$卷积，在计算量上仅有少量的增加。

• 构建一个缩放策略来生产不同计算资源的模型，论文发现宽度扩展对网络增益不大，于是仅考虑深度和输入分辨率的缩放。按前面说的，以倍数形式对基础网络进行深度扩展，同时缩放分辨率，使其训练和测试速度能达到上一个量级的一半。

• 当网络体积增大时，加强正则化强度。通过实验发现，调整weight decay和stochastic depth rate（训练过程随机使某些block的残差分支失效）都没有很大的收益，于是通过加大dropout的drop rate来达到正则化的目的。由于网络缺少BN的显示正则化，所以这一步是十分重要的，防止过拟合的出现。

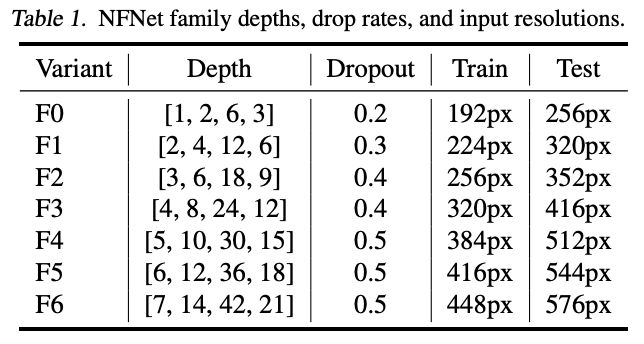
  根据上述的修改，得出的NFNet系列的各参数如表1所示。这里网络的最后有全局池化层，所以训练和测试的分辨率可以不一样。

Experiment

---

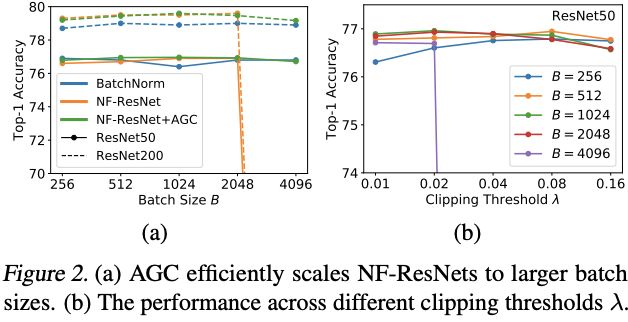
  对比AGC在不同batch size下的效果，以及$\lambda$与batch size的关系。

  在ImageNet对比不同大小的网络的性能。

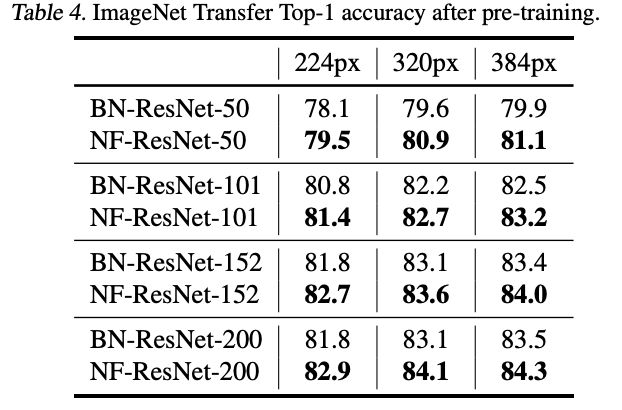
  基于ImageNet的10 epoch预训练权重，进行NF-ResNet改造并Fine-tuning，性能如表4所示。

Conclusion

---

  论文认为Batch Normalization并不是网络的必要构造，反而会带来不少问题，于是开始研究Normalizer-Free网络，希望既有相当的性能也能支持大规模训练。论文提出ACG梯度裁剪方法来辅助训练，能有效防止梯度爆炸，另外还基于NF-ResNet的思想将SE-ResNet改造成NFNet系列，可以使用4096的超大batch size进行训练，性能超越了Efficient系列。

 

 
 
 

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】